From an external point P, a tangent PQ is drawn to a circle, with centre O, touching the circle at Q. If the distance of P from the centre is 13 cm and the length of the tangent PQ is 12 cm, then the radius of the circle is:
एक बाहरी बिंदु P से, केंद्र O वाले एक वृत्त पर एक स्पर्श रेखा PQ खींची जाती है, जो वृत्त को Q पर स्पर्श करती है | यदि केंद्र से P की दूरी 13 सेमी है तथा स्पर्श रेखा PQ की लंबाई 12 सेमी है, तो वृत्त की त्रिज्या कितनी होगी ?
3 cm
5 cm
10 cm
12.5 cm
To find the radius of the circle, we can use the relationship between the radius, the distance from the center to the external point, and the length of the tangent.
1. Identify the given values:
- Distance from point P to center O (PO) = 13 cm
- Length of the tangent PQ = 12 cm
2. Use the Pythagorean theorem:
Since the tangent PQ is perpendicular to the radius OQ at point Q, we can form a right triangle OPQ, where:
- OP is the hypotenuse,
- OQ is one leg (the radius),
- PQ is the other leg (the length of the tangent).
According to the Pythagorean theorem:
OP2=OQ2+PQ2
3. Substitute the known values:
132=OQ2+122
169=OQ2+144
4. Solve for OQ^2:
OQ2=169−144
OQ2=25
5. Find OQ (the radius):
OQ=√25=5 cm
Thus, the radius of the circle is 5 cm.
---
- Distance from point P to center O (PO) = 13 cm
- Length of the tangent PQ = 12 cm
Since the tangent PQ is perpendicular to the radius OQ at point Q, we can form a right triangle OPQ, where:
- OP is the hypotenuse,
- OQ is one leg (the radius),
- PQ is the other leg (the length of the tangent).
OP2=OQ2+PQ2
132=OQ2+122
169=OQ2+144
OQ2=169−144
OQ2=25
OQ=√25=5 cm
Topper's Solved these Questions
Similar Questions
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
View SolutionA point is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
View Solution
Knowledge Check
Length of a chord PQ of a circle with centre O is 4 cm. If the distance of PQ from the centre of circle is 2 cm, then the length of the diameter is:
A2√2cm.B3√2cm.C5√2cm.D4√2cm.From a point Q, the length of the tangent to a circle is 12 cm and the distance of Q from the centre is 13 cm. The radius of the circle is 13 cm. The radius of the circle is :
A12 cmB13 cmC5 cmDNone of theseFrom an external point Q, the length of tangent to a circle is 12 cm and the distance of Q from the centre of circle is 13 cm. The radius of circle (in cm) is
A10B5C12D7
A point P is at a distance of 29cm from the centre of a circle of radius 20cm. Find the length of the tangent drawn from P to the circle.
View SolutionA point P is 13cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
View SolutionFrom a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
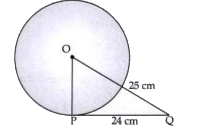
View SolutionIn From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
View SolutionA point P is 25 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
View Solution
