A, B, C are three points so that AB = 4 cm, BC = 6 cm and AC = 10 cm. The number of circles passing through the points A, B, C is:
A, B, C तीन बिंदु है इस प्रकार है की AB = 4 सेमी, BC = 6 सेमी और AC = 10 सेमी। अंक A, B, C से गुजरने वाले वृत्त की संख्या है:
3
0
2
1
To solve the problem, we need to determine how many circles can pass through the points A, B, and C given the distances AB = 4 cm, BC = 6 cm, and AC = 10 cm.
Step 1: Check if a triangle can be formed
To determine if a triangle can be formed with the given sides, we use the triangle inequality theorem. According to this theorem, the sum of the lengths of any two sides must be greater than the length of the third side.
- We have three sides:
- AB = 4 cm
- BC = 6 cm
- AC = 10 cm
Now, we will check the triangle inequalities:
1. Check AB + BC > AC
- 4 cm + 6 cm > 10 cm
- 10 cm > 10 cm (This is not true)
2. Check AB + AC > BC
- 4 cm + 10 cm > 6 cm
- 14 cm > 6 cm (This is true)
3. Check AC + BC > AB
- 10 cm + 6 cm > 4 cm
- 16 cm > 4 cm (This is true)
Since the first condition (AB + BC > AC) is not satisfied, we conclude that a triangle cannot be formed with these sides.
Step 2: Determine the number of circles
Since a triangle cannot be formed, there are no three non-collinear points A, B, and C. Therefore, it is impossible to draw a circle that passes through these points.
Conclusion
The number of circles passing through the points A, B, and C is 0.
---
To determine if a triangle can be formed with the given sides, we use the triangle inequality theorem. According to this theorem, the sum of the lengths of any two sides must be greater than the length of the third side.
- AB = 4 cm
- BC = 6 cm
- AC = 10 cm
- 4 cm + 6 cm > 10 cm
- 10 cm > 10 cm (This is not true)
- 4 cm + 10 cm > 6 cm
- 14 cm > 6 cm (This is true)
- 10 cm + 6 cm > 4 cm
- 16 cm > 4 cm (This is true)
Since a triangle cannot be formed, there are no three non-collinear points A, B, and C. Therefore, it is impossible to draw a circle that passes through these points.
The number of circles passing through the points A, B, and C is 0.
Topper's Solved these Questions
Similar Questions
In the given figure, ABCD is a rectangle and P is a point on DC such that BC=24 cm, DP =10 cm, and CD =15 cm. If AP produced intersects BC produced at Q. Find the length of AQ.
दी गयी आकृति में, ABCD एक आयत है और P, DC पर एक बिंदु इस प्रकार है कि BC = 24 सेमी, DP = 10 सेमी, और CD = 15 सेमी। यदि AP और BC को बढ़ाया जाता है जो Q पर तिच्छेदित करते है तो AQ की लंबाई ज्ञात कीजिए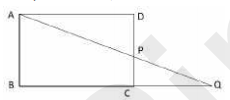 View Solution
View SolutionIn ∠ABC, AB=AC and D is a point on BC. If BD = 5cm, AB =12 cm and AD = 8 cm, then the length of CD is:
त्रिभुज ABC में, AB=AC है और D, BC पर स्थित एक बिंदु है | यदि BD =5 सेमी, AB = 12 सेमी और AD = 8 सेमी है, तो CD की लंबाई ज्ञात करें |View Solution
Knowledge Check
- Question 1 - Select One
If AB =112cm, BC=16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
A90∘B120∘C60∘D150∘
Two chords AB and CD of a circle intersect at a point P inside the circle. If AB = 7cm , PC = 2 cm and AP = 4 cm, then CD is equal to:
एक वृत्त की दो जीवाएं AB और CD वृत्त के भीतर बिंदु P पर एक दूसरे को काटती हैं | यदि AB = 7 सेमी, PC = 2 सेमी और AP = 4 सेमी है, तो CD किसके बराबर होगा ?View SolutionIn △ABC ,D is a median from A to BC, AB = 6cm , AC =8cm and BC = 10cm The length of median AD (in cm ) is :
triangle ABC में, D, A से BC पर एक पर स्थित माध्यिका है।, AB = 6 सेमी, AC=8 सेमी और BC = 10 सेमी है। माध्यिका AD की लंबाई (सेमी में) हैView SolutionIn △ABD, C is the midpoint of BD. If AB = 10 cm, AD = 12 cm and AC = 9 cm, then BD =?
त्रिभुज ABD में, C, BD का मध्य बिंदु है | यदि AB = 10 सेमी, AD = 12 सेमी और AC = 9 सेमी है, तो BD = ?View SolutionThe bisector of ∠B in △ABC meets AC at D. If AB = 10 cm, BC= 11 cm and AC = 14 cm, then the length of AD is:
△ABC में ∠B का समद्विभाजक AC से D पर मिलता है | यदि AB =10 सेमी, BC = 11 सेमी और AC =14 सेमी है, तो AD की लंबाई क्या होगी ?View SolutionIn△ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is : △ABC में, AB = 6 सेमी, AC = 8 सेमी, और BC = 9 सेमी। माध्यिका AD की लम्बाई क्या होगी :
View SolutionA circle inscribed in a triangle ABC touches its sides AB, BC and AC at the points D, E and F, respectively. If AB = 18cm, BC = 15cm and AC = 13 cm then the value of of AD+BE+CF is:
एक त्रिभुज ABCमें अंकित एक वृत्त क्रमशः AB, BC और AC के भुजाओं D, E और F को स्पर्श करता है। यदि AB = 18 सेमी, BC = 15 सेमी और AC = 13 सेमी है तो AD+ BE+ CF का मान है:View Solution△ABC~△EDF and ar(△ABC):ar(△DEF)=4:9. If AB = 6 cm, BC = 8 cm and AC = 10 cm, then DF is equal to :
△ABC~△EDF और ar(△ABC):ar(△DEF)=4:9 है। यदि AB = 6 सेमी, BC = 8 सेमी तथा AC = 10 सेमी है, तो DF का मान क्या होगा ?View Solution

