The marks of Eleven students in ascending order for a test are given below with Median as 36, the value of k is:
नीचे एक परीक्षा में ग्यारह छात्रों के द्वारा प्राप्त किये गए अंक आरोही क्रम में दिए गए हैं जिनकी मध्यिका 36 है |k का मान है : 10, 12, 16, 25, 28, k + 3, k + 5,
43, 45, 47, 53.
36
37
35
33
To find the value of k in the given set of marks, we can follow these steps:
Step 1: Understand the median for an odd number of observations
The median is the middle value in a sorted list of numbers. For a set of n observations where n is odd, the median can be found using the formula:
Median=Value at position (n+12)
Step 2: Identify the number of students
In this case, we have 11 students, so n=11.
Step 3: Calculate the position of the median
Using the formula:
Position of median=11+12=122=6
Thus, the median is the 6th term in the ordered list.
Step 4: Identify the 6th term
From the given marks in ascending order:
10,12,16,25,28,k+3,k+5,43,45,47,53
The 6th term is k+3.
Step 5: Set up the equation for the median
We know from the problem that the median is 36. Therefore, we can set up the equation:
k+3=36
Step 6: Solve for k
To find k, we subtract 3 from both sides:
k=36−3
k=33
Conclusion
The value of k is 33.
---
The median is the middle value in a sorted list of numbers. For a set of n observations where n is odd, the median can be found using the formula:
Median=Value at position (n+12)
In this case, we have 11 students, so n=11.
Using the formula:
Position of median=11+12=122=6
Thus, the median is the 6th term in the ordered list.
From the given marks in ascending order:
10,12,16,25,28,k+3,k+5,43,45,47,53
The 6th term is k+3.
We know from the problem that the median is 36. Therefore, we can set up the equation:
k+3=36
To find k, we subtract 3 from both sides:
k=36−3
k=33
The value of k is 33.
Topper's Solved these Questions
Similar Questions
The marks of Nine students in ascending order for a test are given below with Median as 34, the value of k is:
नीचे एक परीक्षा में नो छात्रों के द्वारा प्राप्त किये गए अंक आरोही क्रम में दिए गये हैं तथा मध्यिका 34 है | k का मान है : 12, 16, k, 28, k + 5, 32, 39, 47, 53.
View SolutionStudy the given histogram that shows the marks obtained by students in an examination and answer the question that follows:
दिए गए हिस्टोग्राम का अध्ययन करें जो एक परीक्षा में छात्रों द्वारा प्राप्त किए गए अंकों को दिखाता है और निम्न प्रश्न का उत्तर दे| The number of students who obtained less than 200 marks is:
The number of students who obtained less than 200 marks is:
200 से कम अंक प्राप्त करने वाले छात्रों की संख्या है:
View Solution
Knowledge Check
The marks of Eleven students in ascending order for a test are given below with Median as 36, the value of k is : 10, 12, 16, 25, 28, k+3, k+5, 43, 45, 47, 53
A36B37C35D33The marks of Nine students in ascending order of a test are given below with Median as 34, the value of k is:
12, 16, k, 28, k + 5, 32, 47, 53, 57A27B30C29D32The average marks obtained by 22 candidates in an examination are 45. The average marks of the first 10 candidates are 55 and those of the last eleven are 40. The number of marks obtained by the eleventh candidate is:
A45B0C50D47.5
The Table given below presents the marks obtained by three students in five examinations.
नीचे दी गयी तालिका पांच परीक्षाओं के तीन विषयों में छात्रों के द्वारा प्राप्त किये गए अंकों को दर्शाती है |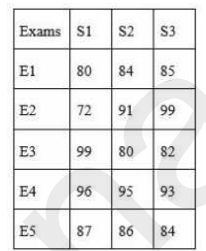 What is the sum of marks obtained by S1 in Exam E4, S2 in Exam E1, S3 in Exam E3 and E5?
What is the sum of marks obtained by S1 in Exam E4, S2 in Exam E1, S3 in Exam E3 and E5?
S1 के द्वारा परीक्षा E4 में, S2 के द्वारा परीक्षा E1 में, तथा S3 के द्वारा परीक्षा E3 और E5 में प्राप्त किये गए अंकों का जोड़ कितना है ?
View SolutionStudy the given histogram that shows the marks obtained by students in an examination and answer the questions that follow
दिए गए हिस्टोग्राम का अध्ययन करें जो एक परीक्षा में छात्रों द्वारा प्राप्त किए गए अंकों को दिखाता है और आने वाले प्रश्नों का उत्तर ज्ञात करे|
The number of students who obtained less than 350 marks is what percent more than the number of students who obtained 400 or more marks?(correct to one decimal place )
350 से कम अंक प्राप्त करने वाले छात्रों की संख्या 400 या अधिक अंक प्राप्त करने वाले छात्रों की संख्या की तुलना में प्रतिशत अधिक है| (एक दशमलव स्थान तक )
View SolutionStudy the given histogram that shows the marks obtained by students in an examination and answer the question that follows:
दिए गए हिस्टोग्राम का अध्ययन करें जो एक परीक्षा में छात्रों द्वारा प्राप्त किए गए अंकों को दिखाता है और निम्न प्रश्न का उत्तर दे|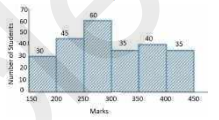 If the total marks obtained by students be represented as a pie chart, then the central angle of thesector representing marks 200 or more but less than 300, is :(correct to one decimal place)
If the total marks obtained by students be represented as a pie chart, then the central angle of thesector representing marks 200 or more but less than 300, is :(correct to one decimal place)
यदि छात्रों द्वारा प्राप्त कुल अंकों को पाई चार्ट के रूप में दर्शाया जाता है, तो 200 या अधिक और 300 से कम अंकों का प्रतिनिधित्व करने वाले क्षेत्र का केंद्रीय कोण है: (एक दशमलव स्थान के लिए सही)
View SolutionStudy the given histogram that shows the marks obtained by students in an examination and answer the question that follows:
दिए गए हिस्टोग्राम का अध्ययन करें जो एक परीक्षा में छात्रों द्वारा प्राप्त किए गए अंकों को दिखाता है और निम्न प्रश्न का उत्तर दे| The number of students who obtained less than 250 marks is what percent more than the number of student who obtained 400 or more marks ?(correct to one decimal place)
The number of students who obtained less than 250 marks is what percent more than the number of student who obtained 400 or more marks ?(correct to one decimal place)
250 से कम अंक प्राप्त करने वाले छात्रों की संख्या 490 या अधिक अंक प्राप्त करने वाले छात्र की संख्या से कितने प्रतिशत अधिक है? (एक दशमलव तक)
View SolutionThe Table given below presents the marks obtained by three students in five examinations.
नीचे दी गयी तालिका पांच परीक्षाओं के तीन विषयों में छात्रों के द्वारा प्राप्त किये गए अंकों को दर्शाती है |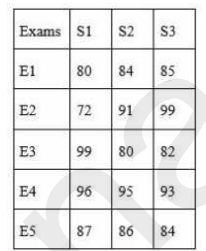 The marks obtained by S1 in Exam E5 is how much percentage (correct up to two places of decimal) more than that obtained by S2 in Exam E3?
The marks obtained by S1 in Exam E5 is how much percentage (correct up to two places of decimal) more than that obtained by S2 in Exam E3?
S1 के द्वारा परीक्षा E5 में प्राप्त किये गए अंक S2 के द्वारा परीक्षा E3 में प्राप्त किये गए अंक से कितने प्रतिशत अधिक ( दो दशमलव स्थान तक) हैं ?
View Solution
