A ball is thrown with a velocity of $20 m s^{- 1}$ at an angle of $30^{\circ}$ above the horizontal from the top of a building 15 m high. Find (take $g = 10 m s^{- 2}$ )
a. the time after which the ball hits the ground.
b. the distance from the bottom of the building at which it hits the ground.
c. the velocity with which the ball hits the ground.
d. the maximum height attained by the ball above the ground.

Text Solution

Verified by Experts

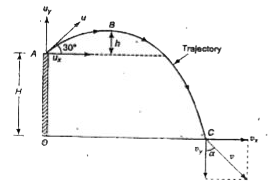
Refere to figure. The horizontal and vertical components of initial velocity are
a. $u_{x} = 20 {cos 30}^{\circ} = 10 \sqrt{3} m s^{- 1}$
$u_{y} = 20 {sin 30}^{\circ} = 10 m s^{- 1}$ (vertically upwards)
Horizontal acceleration $a_{x} = 0$ and vertical acceleration $a_{y} = - 10 m s^{- 2}$ (vertically downwards)
Vertical displacement S=H=-15m
Since the vertical and horizontal motions are independent of each other, for vertical motion.
$S = u_{y} t + \frac{1}{2} a_{y} t^{2}$
$\Rightarrow - 15 = 10 t + \frac{1}{2} \times (- 10) t^{2}$
$\Rightarrow - 15 = 10 t - 5 t^{2}$
$\Rightarrow t^{2} - 2 t - 3 = 0$
$\Rightarrow t = - 1 s$ or $3 s$
Since t=-1 s is not possible, the ball with strike ground at point C after 3 seconds.
b.Horizontal range $R = O C = u_{x} t = 10 \sqrt{3} \times 3 = 30 \sqrt{3} m$
Vertical velocity component at C is $_(y) = u_{y} + a_{y} t = 10 - 10 \times 3 = - 20 m s^{- 1}$
The negative sign shows that the ball is moving downwards.
Resultant velocity $v = \sqrt{v_{x}^{2} + v_{y}^{2}}$
$= \sqrt{{(10 \sqrt{3})}^{2} + {(20)}^{2}} = 10 \sqrt{7} m s^{- 1}$
$tan α = \frac{v_{x}}{∣ ∣ v_{y} ∣ ∣} = \frac{10 \sqrt{3}}{20} = \frac{\sqrt{3}}{2}$
$\Rightarrow α = {tan}^{- 1} (\frac{\sqrt{3}}{2})$ with the vertical.
d. Maximum height attained above the ground is $h_{max} = h + H$
$= \frac{u^{2} {sin}^{2} θ}{2 g} + H = \frac{{(20)}^{2} {sin}^{2} (30^{\circ})}{2 \times 10} + 15 = 5 + 15 = 20 m$

Updated on:21/07/2023