Wheel A of radius 10 cm is coupled by a belt B to wheel C of radius 30 cm as shown in figure. Wheel A increases its angular speed from rest at a uniform rate of 1.57rad/s2. Determine the time for wheel C to reach a rotational speed of 100 rev/min assuming that the belt does not slip.
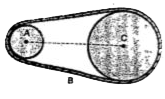
As the belt does not slip vA=vC
i.e. rAωA=rCωC [as v=rω]
Here rA=10cm rC=30cm
and ωc=(2π×10060) rad/s
so 10ωA=30×2π×10060
i.e. ωA=10π rad/s
No from 1st equation of rotational motion i.e. ω=ω0+αt
t=ωα [as ω0=θ]
i.e. t=10×π1.57=20sec
Similar Questions
In Fig. 10-54, wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 2.0rad/s2. Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip.
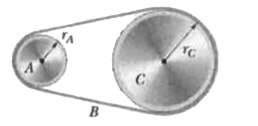
View SolutionIn figure wheel A of radius rA=10cm is coupled by belt B to wheel C of radius rC=25cm. The angular speed of wheel A is increased from rest at a constant rate of 1.6rad/s2. Find the time needed for wheel C to reach an angular speed of 12.8rad/s, assuming the belt does not slip.
 .
.
View Solution
Knowledge Check
A wheel having radius 10 cm is coupled by a belt to another wheel of radius 30 cm . 1st wheel increases its angular speed from rest at a uniform rate of 1.5rads−2 . The time for 2nd wheel to reach a rotational speed of 100rev/min is ... (assume that the belt does not slip )
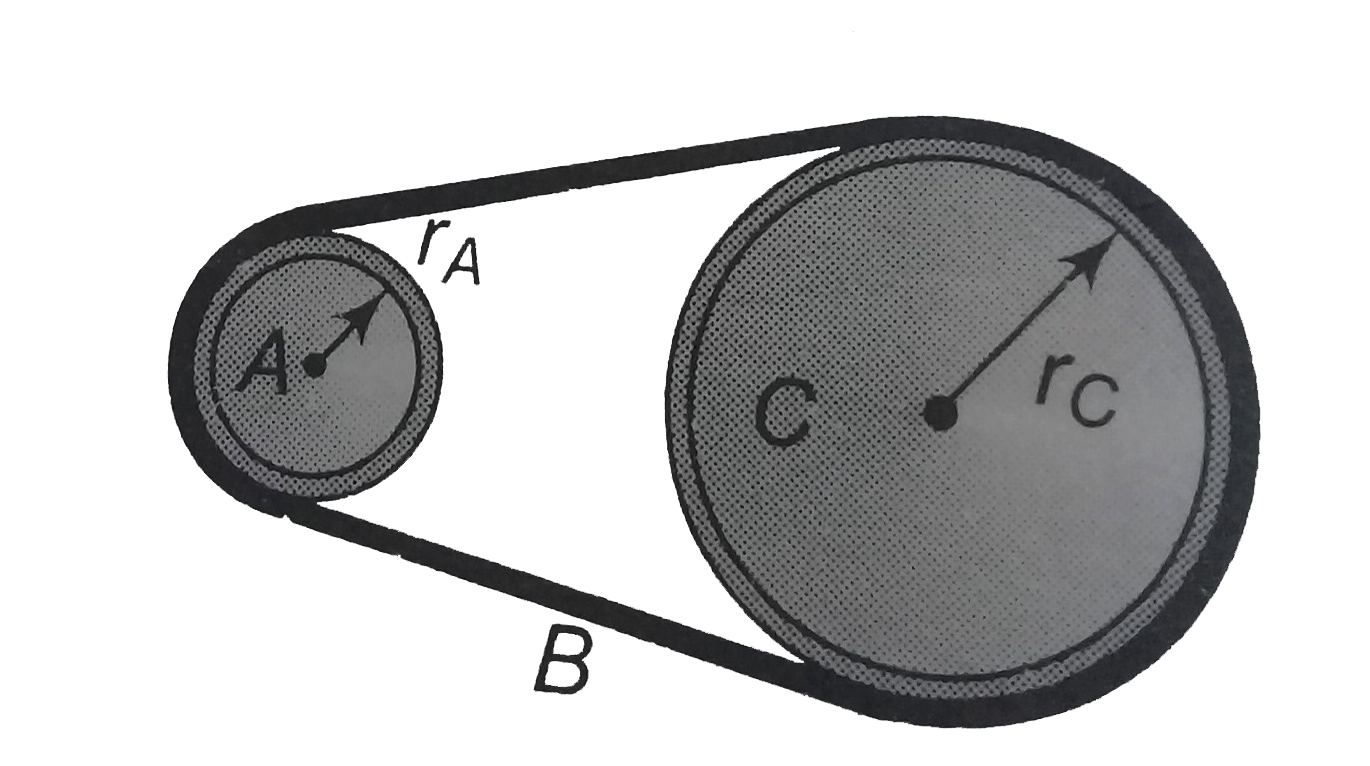
A20 secB10 secC1.5 secD15secIn figure whell A of radius rA=10cm is coupled by belt B to whell C of radius rC=25cm. The angular speed of whell A is increased from rest at a constant rate of 1.6rad/s2. Find the time needed for whell C to reach an angular speed of 12.8rad/s, assuming the belt does not slip.
 .A15 sB12.5 sC20 sD10 s
.A15 sB12.5 sC20 sD10 sA wheel increases its speed from 60 rpm to 120 rpm in 10 s. Number of rotation made by it in 10 s is
A10B15C25D20
Wheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]

View SolutionWheel A of radius rA=10cm is coupled by a belt C to another wheel of radius rB=25cm as in the figure. The wheels are free to rotate and the belt does not slip . At time t=0 wheel A increases it's angular speed from rest at a uniform rate π/2rad/sec2 Find the time in which wheel B attains a speed of 100r±[ Hint :vA=vB]

View SolutionA wheel of radius 15cm is rotating about its axis at angluar speed of 20rad/s. Find the linear speed and total acceleration of a point on the rim.
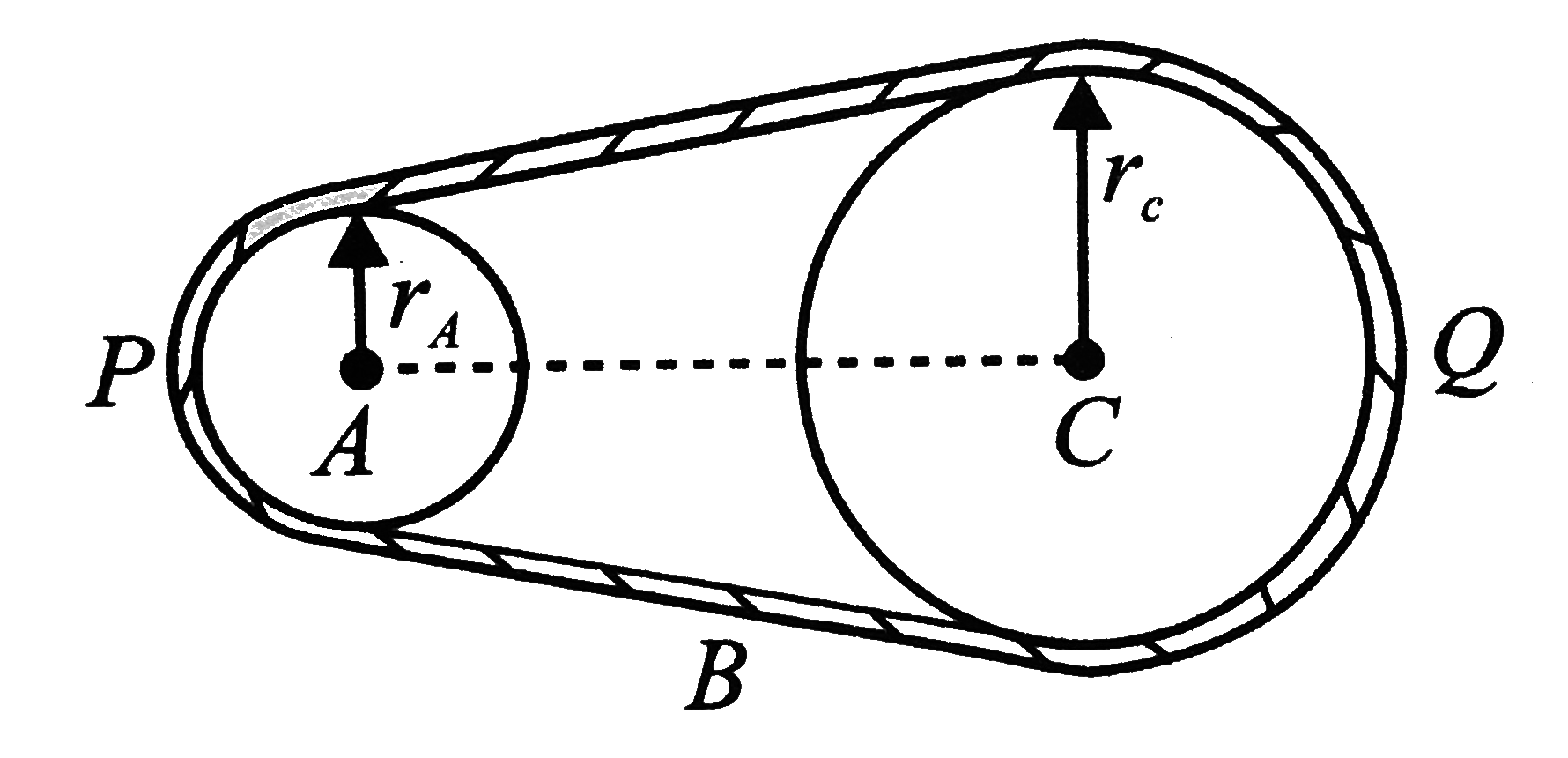
View SolutionTwo wheels A and C are connected by a belt B as shown in figure. The radius of C is three times the radius of A. What would be the ratio of the rotational inertias (IC/IA) if both the wheels have the same rotational kinetic energy?
View SolutionA belt passes over a wheel of radius 25 cm. If a point on the belt has a speed of 5m/s, the belt is moving with an angular velocity of
View Solution
