Two spherical bodies of masses M and 5 M and radius Rand 2R respectively in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before collision is
2.5 r
4.5 R
7.5 R
1.5 R
The correct Answer is:C
Distance between the centres of spheres=12 R
∴ Distance between their surfaces =12R-(2R+R)=9R
Since there is no external force, hence centre of mass must remain unchanged and hence
⇒m1r1=m2r2⇒Mx=5M(9R−x) (where) x = distance covered by smaller body.
x = 7.5 R
Similar Questions
Two spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionTwo spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
View Solution
Knowledge Check
Two spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
A2.5 RB4.5 RC7.5 RD1.5 RTwo spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
A15R2B13R2C10RD17R2Two spherical bodies of masses m and 4m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 15 R. If they attract each other due to gravitational force only, then the distance covered by smaller sphere just before collision will be
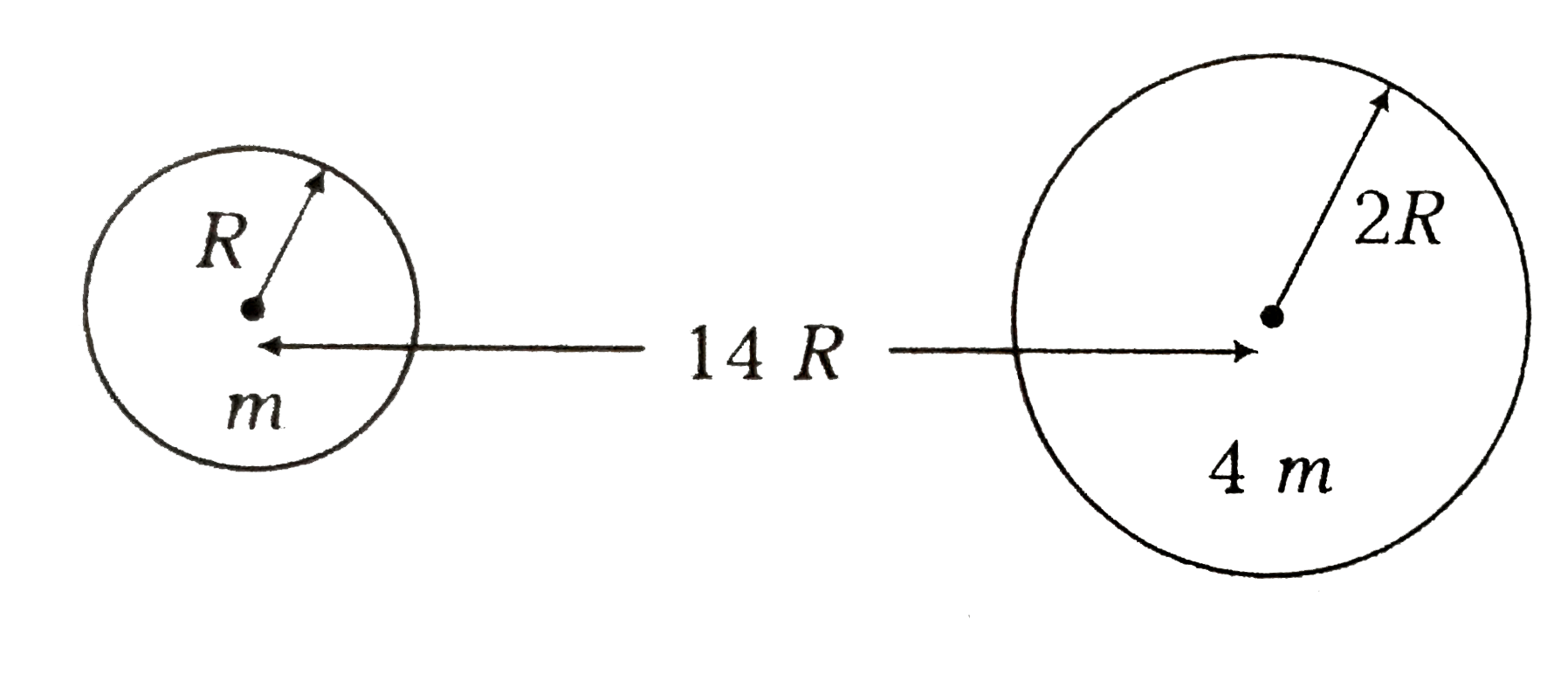 A5 RB9.6 RC2.5 RD6 R
A5 RB9.6 RC2.5 RD6 R
Two spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
View SolutionTwo spherical bodies of masses m and 6m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 10 R . If they attract each other due to gravitational force only , then the distance covered by smaller sphere just before collisions will be
View SolutionTwo spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
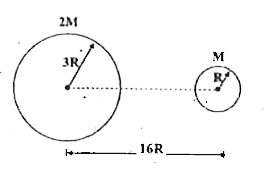
View SolutionTwo spherical bodies of masses m and 6m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 10 R . If they attract each other due to gravitational force only , then the distance covered by smaller sphere just before collisions will be
View SolutionWhich of the following statements is true ?
(i) A car of mass M is tied by one end of a massless rope of length 10m. The other end of the rope is in the hands of a man of mass M. The entire system is on a smooth horizontal surface.The man is at x=0 and the cart at x=10m. If the man pulls the cart by the rope, the man and the cart will meet at the point x=5m.
(ii) Two spherical bodies of mass M and 5M and radii R and 2R, respectively , are released in free space with initial separation between their centers equal to 12R. If they attract each other due to the gravitational force only , then the distance covered by the smaller body just before collision is 7.5R.
(iii) Two skaters A and B , having masses 40kg and 60kg , respectively stand facing each other 10m apart on a horizontal smooth surface. They pull on a rope stretched between them , the distance covered by A, when skaters meet is 6m.
(iv) A ballon (mass M) is attached to light rope of length L. To the other end of the rope a boy (mass m) is hanging in air. The system is at rest. The distance travelled by the balloon (in downward direction) when the boy touches the ballon is MLM+m.
View Solution
