A steel wire of diameter and length 1m is clamped firmly at two points A and B which are 1m apart and in the same plane. A body is hung from the middle point of the wire such that the middle point sags 1cm lower from the original position. Calculate the mass of the body. Given that Young's modulus of the material of wire is .
As shown in figure, for equilibrium of mass M,
…….(i)

But from figure,
any by definition of Young.s modulus,
.......(iii)
So substituting the values of and from Eqns. (ii) and (iii) in Eqn, (i), we get
, i.e., .............(iv)
Now as here ,
and
So,
Similar Questions
A steel wire of diameter 0.8 mm and length 1m is clamped firmly at two points P and Q which are one metre apart and in the same horizontal plane. A body is hung from the middle point of the wire, such that the middle point sags one cm lower from the original position as shown in figure. Calculate the mass of the body. Y=2×1011N/m2.
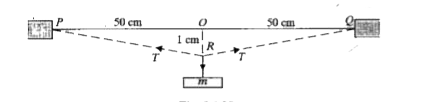
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View Solution
Knowledge Check
A load of 3kg produces an extension of 1.5mm in a wire of length 3m and diameter 2mm. Young's modulus of the material of the wire is
A1.87×1010Nm−2B3.5×1010Nm−2C15×1010Nm−2D2.5×1010Nm−2
(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View SolutionA steel of area of cross-section A and length 2L is calmped family between two rigid supports separated by a distance '2L'. A body is hung from the middle point sags by a distance x. Calculate the mass of the body body and the angle made by the string with the horizontal. (Young's modulus of Steel =Y)
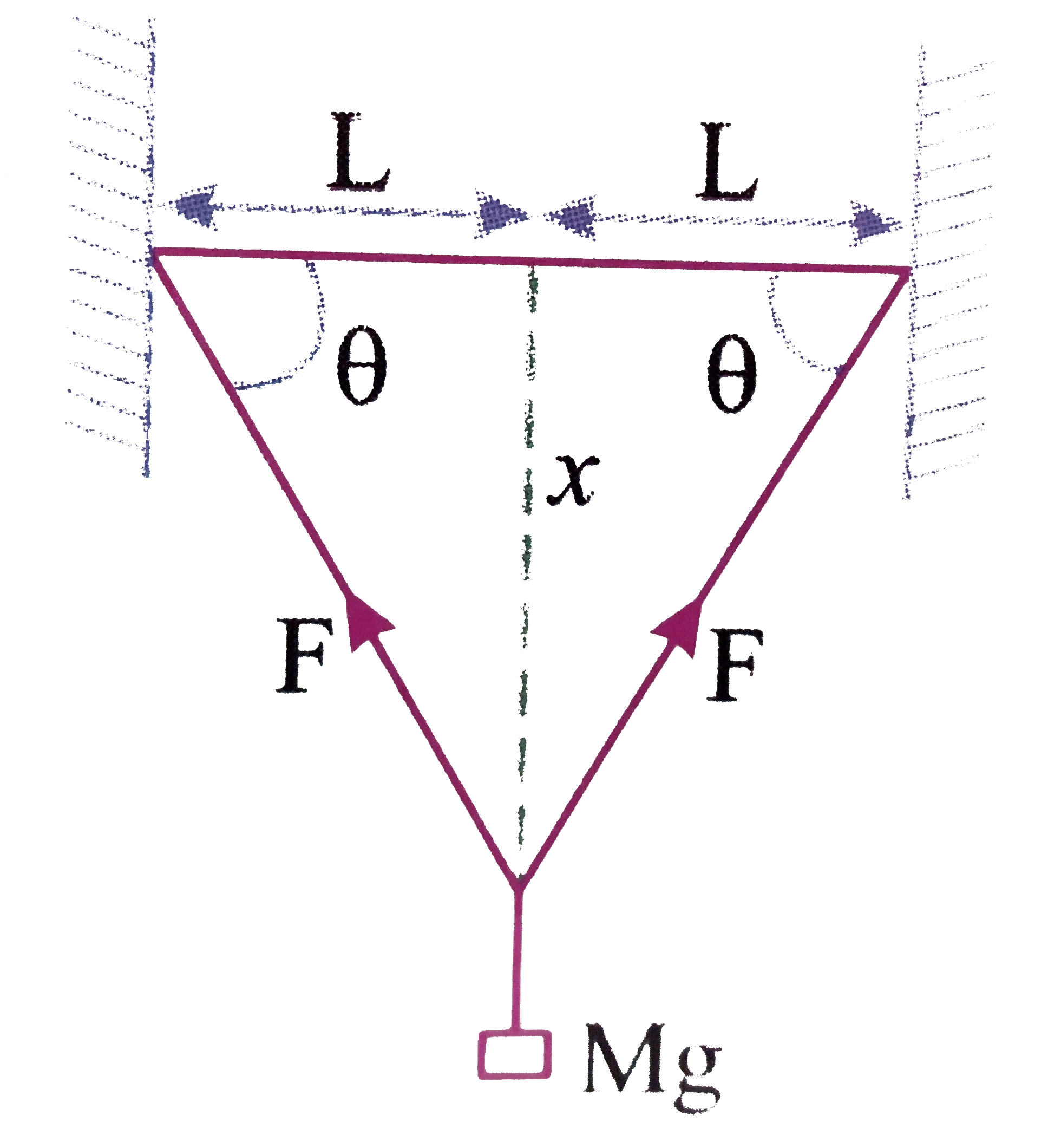
View SolutionA steel wire of length 4 m and diameter 5 mm is stretched by kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View SolutionA steel wire of length 600cm and diameter 1.2 mm is stretched through 4 mm by a load. Calculate the work done. Young's modulus of steel =2×1011Nm−2.
View SolutionA steel wire of diameter d=1.0mm is stretched horizontally between two clamps located at the distance l=2.0m from each other. A weight of mass m=0.25kg is suspended from the mid-point O of the wire. What will the resulting descent of the point O be in centrimetres?
View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View SolutionA steel wire of length 1m and diameter 4mm is stretched horizontally between two rigit supports attached to its end. What load would be required to be hung from the mid-point of the wire to produce a depression of 1cm? (Y=2×1011Nm−2)
View Solution
