An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔV(VΔT) varies with temperature as:
A

B

C

D

Text Solution
The correct Answer is:C
At constant pressure, V∝T⇒ΔV∝ΔT
∴ΔVV=ΔTT,T(ΔVVΔT)= constant , T.δ= constant
∴ Graph of δ−T is a rectangular hyperbola.
|
Similar Questions
Knowledge Check
An ideal gas is initially at temperature T and volume V . Its volume is increased by ΔV due to an increase in temperature Δ , pressure remaining constant . The quantity δ=ΔV/VΔT varies with temperature as
A B
B C
C D
D
An ideal gas is initially at temperature T and volume V. It's volume increases by ΔV due to an increase in temperature of ΔT, pressure remaining constant. The quantity μ=ΔVVΔT varies with temperature as -
A B
B C
C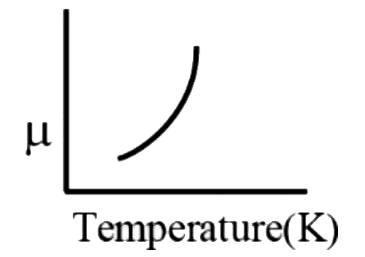 D
D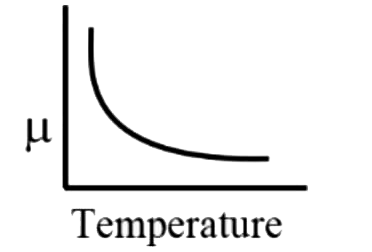
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A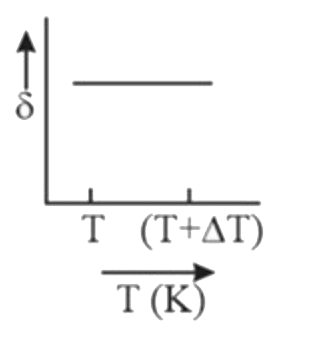 B
B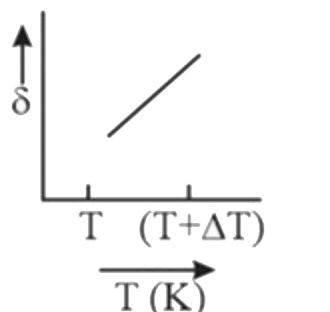 C
C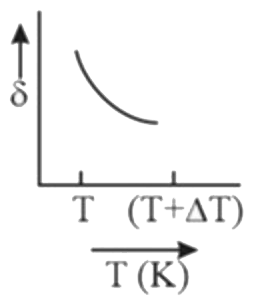 D
D
By increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionThe pressure exerted by 12g of an ideal gas at temperature t∘C in a vessel of volume Vlitre is 1atm. When the temperature is increased by 10∘C at the same volume, the pressure increases by 10%. Calculate the temperature t and volume V. (Molecular weight of the gas is 120).
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View SolutionBy increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View Solution
