An ideal gas is initially at temperature T and volume V. ITS volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔV/VΔT varies with temperature as


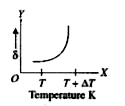
The correct Answer is:C
To solve the problem, we will analyze the behavior of an ideal gas when its volume increases due to a change in temperature while keeping the pressure constant. We will derive the relationship between the given quantities step by step.
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is the temperature.
2. Initial Conditions:
Initially, the gas is at temperature T and volume V. When the temperature increases by ΔT, the volume increases by ΔV while the pressure remains constant.
3. Express Volume in Terms of Temperature:
Since pressure is constant, we can express the volume as:
V=nRPT
4. Change in Volume:
When the temperature increases by ΔT, the new volume V′ can be expressed as:
V′=nRP(T+ΔT)=nRPT+nRPΔT
5. Calculate the Change in Volume:
The change in volume ΔV is given by:
ΔV=V′−V=nRPΔT
6. Formulate the Quantity δ:
We need to find the quantity:
δ=ΔVVΔT
Substituting ΔV and V into this equation:
δ=nRPΔTnRPTΔT
Simplifying this gives:
δ=1T
7. Analyze the Variation of δ with Temperature:
The expression δ=1T indicates that δ varies inversely with temperature T.
8. Graphical Representation:
As T approaches 0, δ approaches infinity, and as T approaches infinity, δ approaches 0. This relationship is characteristic of a rectangular hyperbola.
Conclusion:
The quantity δ varies with temperature as:
δ∝1T
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is the temperature.
Initially, the gas is at temperature T and volume V. When the temperature increases by ΔT, the volume increases by ΔV while the pressure remains constant.
Since pressure is constant, we can express the volume as:
V=nRPT
When the temperature increases by ΔT, the new volume V′ can be expressed as:
V′=nRP(T+ΔT)=nRPT+nRPΔT
The change in volume ΔV is given by:
ΔV=V′−V=nRPΔT
We need to find the quantity:
δ=ΔVVΔT
Substituting ΔV and V into this equation:
δ=nRPΔTnRPTΔT
Simplifying this gives:
δ=1T
The expression δ=1T indicates that δ varies inversely with temperature T.
As T approaches 0, δ approaches infinity, and as T approaches infinity, δ approaches 0. This relationship is characteristic of a rectangular hyperbola.
The quantity δ varies with temperature as:
δ∝1T
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - INTERNAL ENERGY
40 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL CONDUCTION
17 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - PROPERTIES OF MATTER (SURFACE TENSION )
23 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
Knowledge Check
If the pressure and the volume of certain quantity of ideal gas are halved, then its temperature
Ais doubledBbecomes one-fourthCremains constantDbecome four timesAs the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
AIncreasesBDecreasesCRemains sameDBecomes half
By increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View SolutionAt constant temperature if the pressure of an ideal gas is increased by 10% then its volume must decrease by
View SolutionAt constant temperature if the pressure of an ideal gas is increased by 10% then its volume must decrease by
View SolutionAs the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
View SolutionWhen volume of system is increased two times and temperature is decreased half of its initial temperature, then pressure becomes ………….
View Solution
