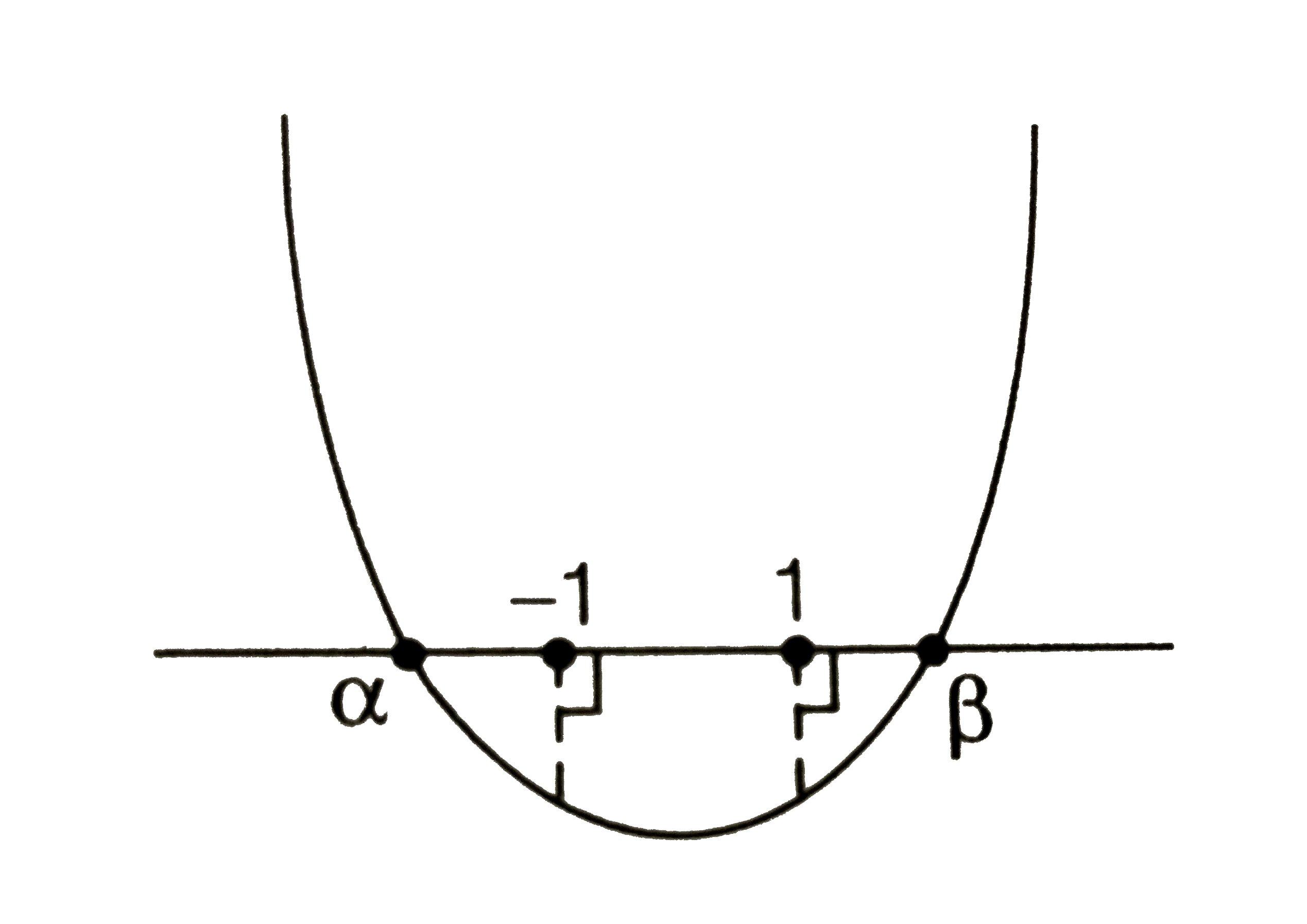
Let a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩1 , then show that 1+ca+∣∣∣ba∣∣∣<0Solution in Gujrati
Since α<−1 and β>1
α+λ=−1 and β=1+μ[λ,μ>0]
Now 1+ca+∣∣∣ba∣∣∣=1+αβ+|α+β|
=1+(−1−λ)(1+μ)+|−1−λ+1+μ|
=1−1−μ−1λ−λμ+|μ−λ|
=−μ−λ−λμ+μ−λ [if μ>λ]
and =−μ−λ−λμ+λ−μ [if λ>μ]
∴1+ca+∣∣∣ba∣∣∣=−2lameda−λμ or −2μ−λμ
On both cases 1+ca+∣∣∣ba∣∣∣<0[∵λ,μ>0]
Aliter
∵ax2+bx+c=0,a≠0
x2+bax+ca=0
Let f(x)=x2+bax+ca
f(−1)<0 and f(1)<0
⇒1−ba+ca<0 and 1+ba+ca<0
Then 1+∣∣∣ba∣∣∣+ca<0
Similar Questions
Let a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩−1 , then show that 1+ca+∣∣∣ba∣∣∣<0
View SolutionIf αandβ are roots of the quadratic equation ax2+bx+c=0 and a+b+c>0,a−b+c>0&c<0,then[α]+[β] is equal to (where [.] denotes the greatest integer function) (a)10 (b) −3 (c) −1 (d) 0
View SolutionIf α is a real root of the quadratic equation ax2+bx+c=0andβ ils a real root of −ax2+bx+c=0, then show that there is a root γ of equation (a/2)x2+bx+c=0 whilch lies between α&β
View SolutionConsider two complex numbers αandβ as α=[(a+bi)/(a−bi)]2+[(a−bi)/(a+bi)]2, where a ,b , in R and β=(z−1)/(z+1),where|z|=1, then find the correct statement: (a)both αandβ are purely real (b)both αandβ are purely imaginary (c)α is purely real andβ is purely imaginary (d)β is purely real and α is purely imaginary
View SolutionIf ax2+(b−c)x+a−b−c=0 has unequal real roots for all c∈R,then
View SolutionIf αandβ are the roots of ax2+bx+c=0andSn=αn+βn, then aSn+1+bSn+cSn−1=0
View SolutionIf αandβ(α<β) are the roots of the equation x2+bx−c=0,whereb<0<c, then 0<α<β b. α<0<β<|α| c. α<β<0 d. α<0<|α|<β
View SolutionLet a,b,c be real. If ax2+bx+c=0 has two real roots αandβ,whereα⟨−1andβ⟩1 , then show that 1+ca+∣∣∣ba∣∣∣<0
View Solution
