When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
![When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum. F=(rhoAV(0))V(0)-(rhoAV(0))V(0)costheta=rhoAV(0)^(2)[1-costheta] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes F=rhoA(V(0)-u)^(2)[1-costheta] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following. Given that cross sectional area of jet =2xx10^(-4)m^(2) velocity of jet V(0)=10m//s density of liquid =1000kg//m^(3) ,mass of cart M=10 kg. Initially (l=0) the force on the cart is equal to](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_C04_E01_199_Q01.png)
F=(ρAV0)V0−(ρAV0)V0cosθ=ρAV20[1−cosθ] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes <br>F=ρA(V0−u)2[1−cosθ] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
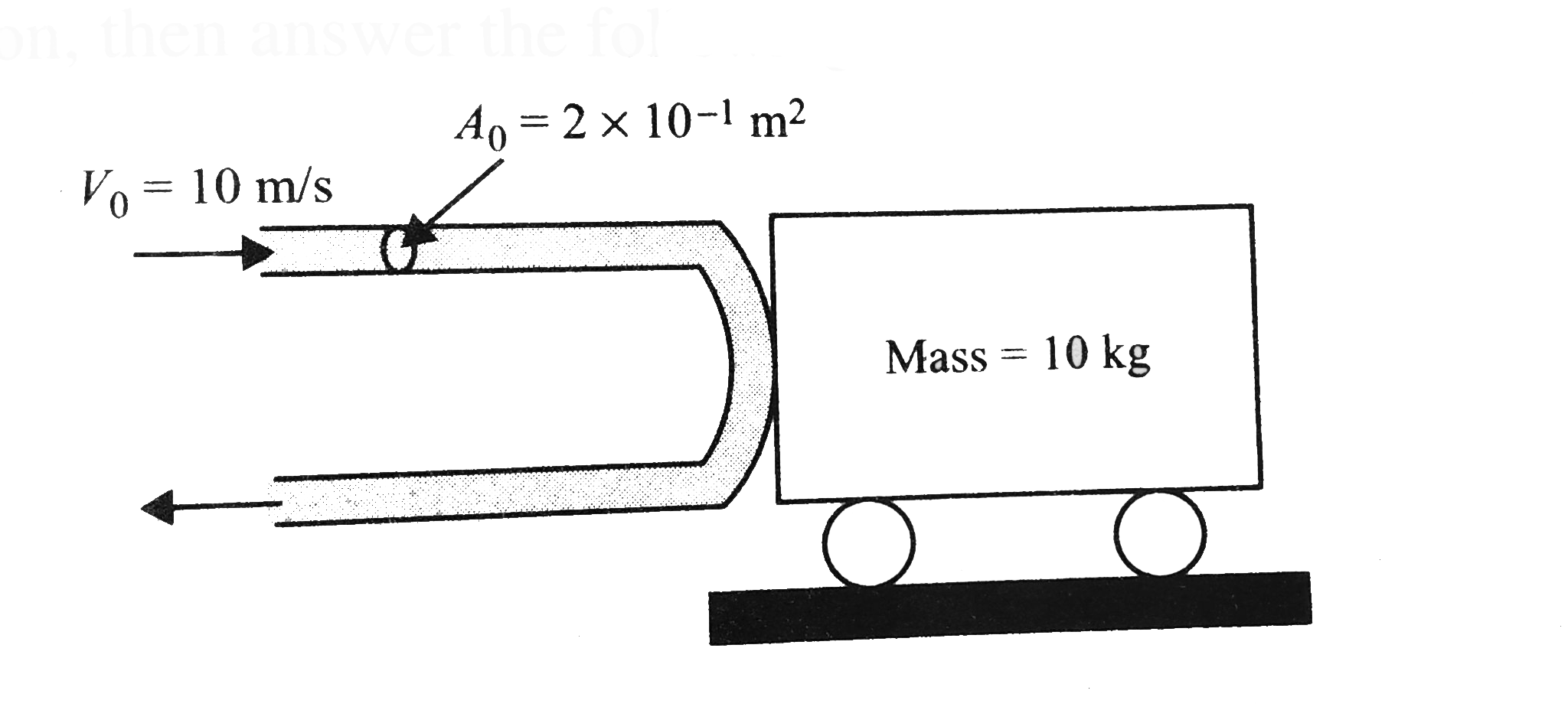
Given that cross sectional area of jet =2×10−4m2 velocity of jet V0=10m/s density of liquid =1000kg/m3 ,mass of cart M=10kg.
Initially (l=0) the force on the cart is equal toSolution in Gujrati
20 N
40 N
80 N
zero
The correct Answer is:B
Step by step video & image solution for When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum. F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes F=rhoA(V_(0)-u)^(2)[1-costheta] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following. Given that cross sectional area of jet =2xx10^(-4)m^(2) velocity of jet V_(0)=10m//s density of liquid =1000kg//m^(3) ,mass of cart M=10 kg. Initially (l=0) the force on the cart is equal to by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Elasticity)
7 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Surface Tension)
5 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
In the figure shown the straing versus stress graph for two values of young's modulus ?
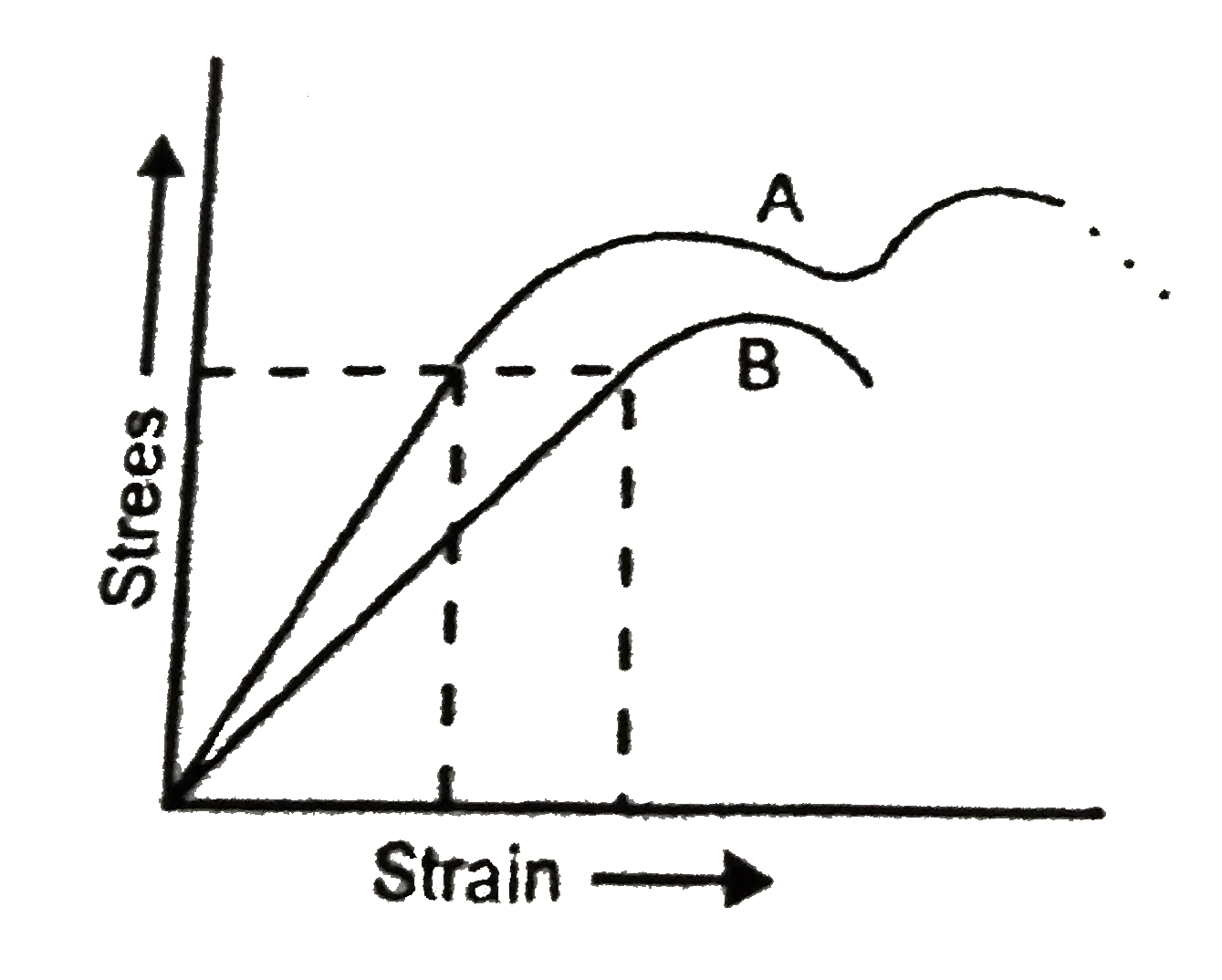
(i) which material is more ductile ? Explain.
(ii) Which material is more brittle ? Explain.
(iii) Which material is stronger ? Explain.
View Solution_E01_194_Q01.png)
PQRS is a rectangular frame of copper wire shown in figure the side RS of the frame is movable. If a soap film is formed on it then what is the diameter of the wire to maintain equilibirum (given surface tension of soap solution =0.045N/m and density of copper =8.96×103kg/m3)
View SolutionStatement-1: A solid sphere and a hollow sphere of same material are floating in a liquid radius of both the spheres are same percentage of volume immersed of both the spheres will be same.
Statement-2: Upthust acts on volume of liquid displaced. It has nothing to do whether the body is solid or hollow.
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
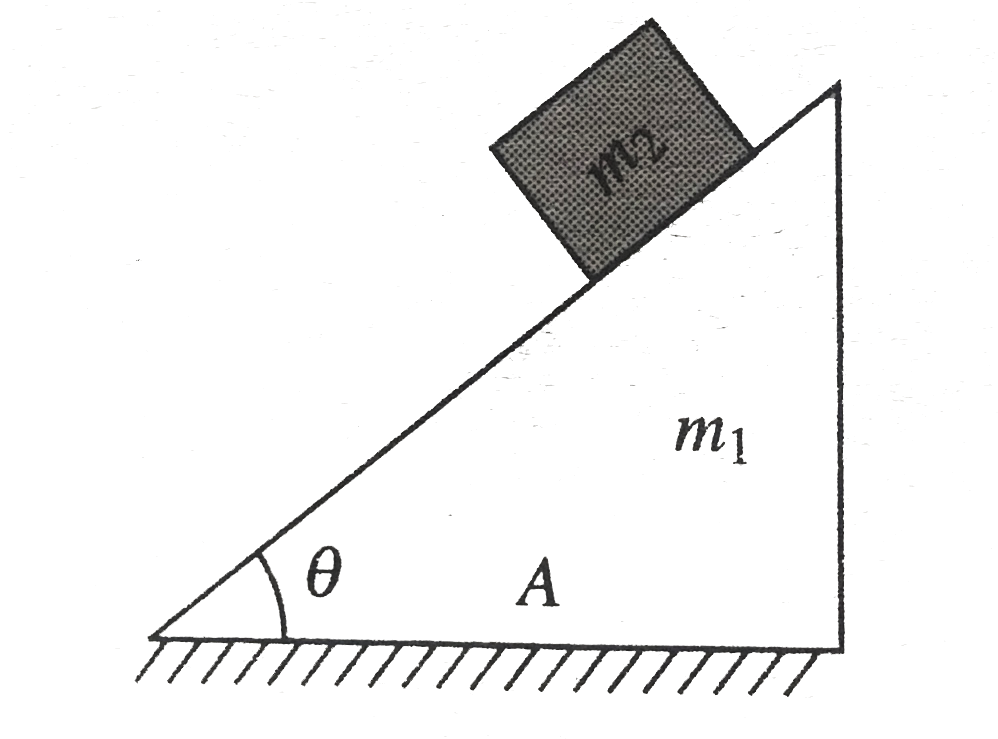
View SolutionIn fig., the mass m2 starts with velocity v0 and moves with constant velocity on the surface. During motion, the normal reaction between the horizontal surface and fixed triangle block m1 is N. Then during motion.
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum. F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u . Then the above equation becomes F=rhoA(V_(0)-u)^(2)[1-costheta] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following. Given that cross sectional area of jet =2xx10^(-4)m^(2) velocity of jet V_(0)=10m//s density of liquid =1000kg//m^(3) ,mass of cart M=10 kg . Initially ( l=0 ) the force on the cart is equal to
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
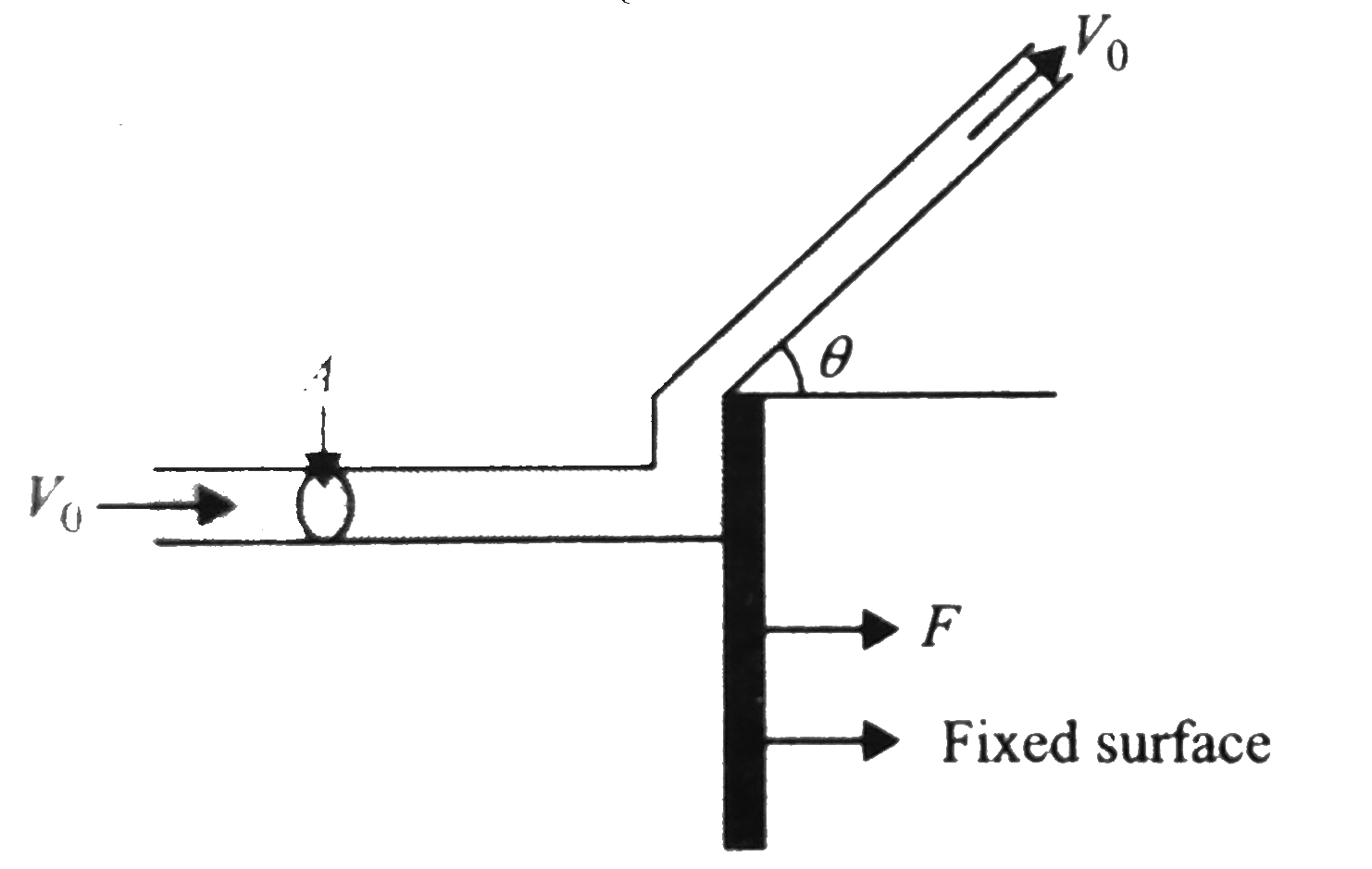
F=(ρAV0)V0−(ρAV0)V0cosθ=ρAV20[1−cosθ] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes <br>F=ρA(V0−u)2[1−cosθ] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
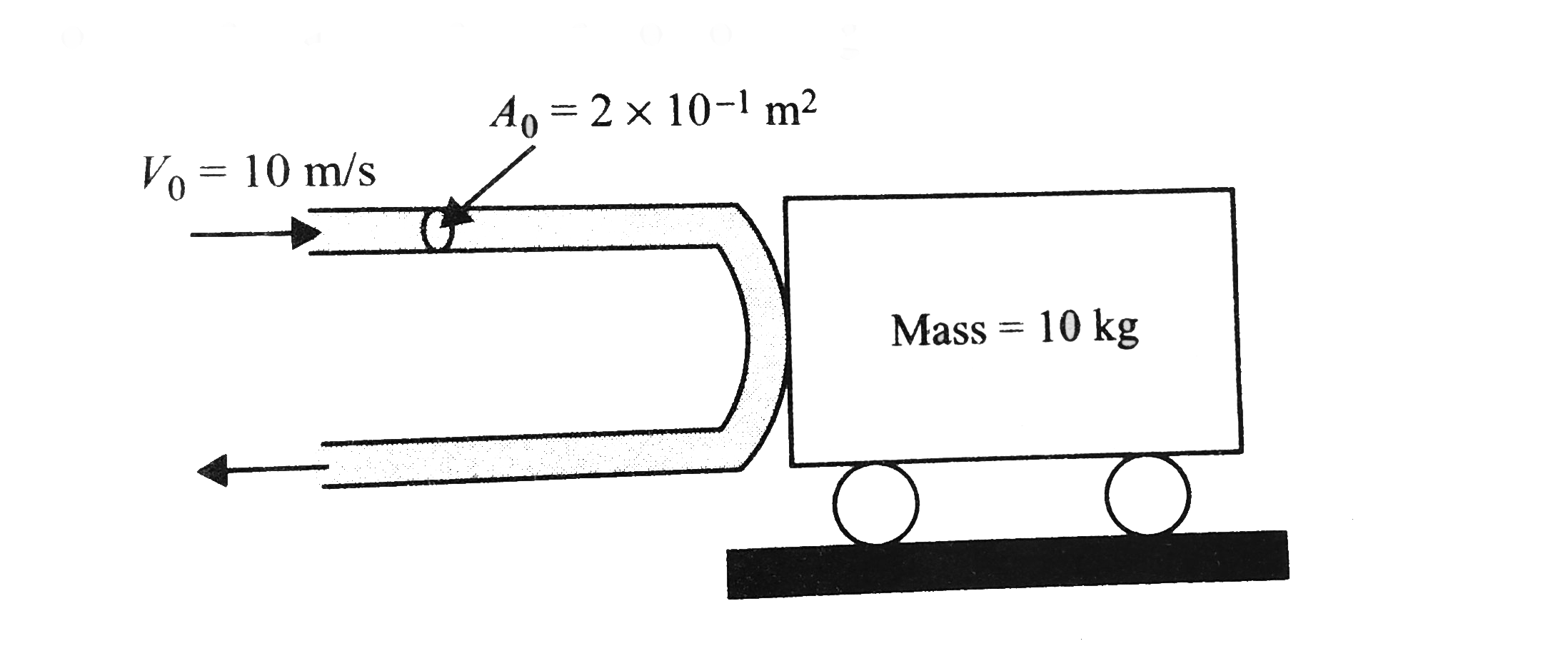
Given that cross sectional area of jet =2×10−4m2 velocity of jet V0=10m/s density of liquid =1000kg/m3 ,mass of cart M=10kg.
Velocity of cart at t=10s is equal to
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum. F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u . Then the above equation becomes F=rhoA(V_(0)-u)^(2)[1-costheta] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following. Given that cross sectional area of jet =2xx10^(-4)m^(2) velocity of jet V_(0)=10m//s density of liquid =1000kg//m^(3) ,mass of cart M=10 kg . The time at which velocity of cart becomes 2 m/s is equal to
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum. F=(rhoAV_(0))V_(0)-(rhoAV_(0))V_(0)costheta=rhoAV_(0)^(2)[1-costheta] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u . Then the above equation becomes F=rhoA(V_(0)-u)^(2)[1-costheta] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following. Given that cross sectional area of jet =2xx10^(-4)m^(2) velocity of jet V_(0)=10m//s density of liquid =1000kg//m^(3) ,mass of cart M=10 kg . The power supplied to the cart when its velocity becomes 5 m//s is equal to
View SolutionThe fraction of a floating object of volume V0 and density d0 above the surface of a liquid of density d will be
View SolutionA sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:

View SolutionA particle moves with initial velocity v_(0) and retardation alphav , where v is velocity at any instant t. Then the particle
View SolutionA sphere moving with a speed v_(0) on a smooth surface suddenly enters on a rough horizontal surface as shown. The angular momentum of the sphere about any point on the surface is conserved.
View SolutionThrust of a liquid always acts ____ to the surface of contact.
View SolutionIn fig., the mass m_(2) starts with velocity v_(0) and moves with constant velocity on the surface. During motion, the normal reaction between the horizontal surface and fixed triangle block m_(1) is N . Then during motion.
View Solution
