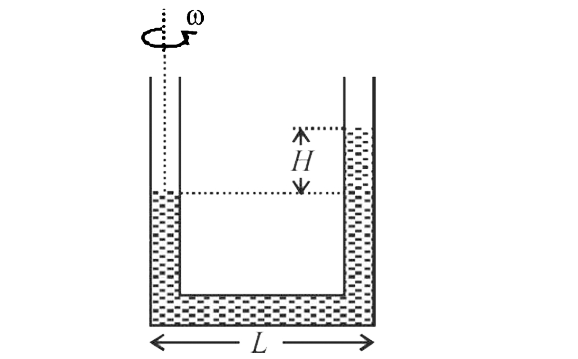
A U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:H=ω2L22g
Step by step video & image solution for A U tube is rotated about one of it's limbs with an angular velocity omega. Find the difference in height H of the liquid (density rho) level, where diameter of the tube dlt lt L. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Assertion Reason)
1 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionSTATEMENT-1: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.
STATEMENT-2: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA U tube is rotated about one of it's limbs with an angular velocity omega . Find the difference in height H of the liquid (density rho ) level, where diameter of the tube dlt lt L .
View SolutionA U-tube rotates with angular velocity ω about the vertical axis AB. What is the difference in fluid level h in terms of ω the radii r1 and r2 and the fluid density ρ?
View SolutionA vertical U -tube is spinned about the vertical axis passing through the left hand limb, with an angular speed omega such that the liquid columns in the limbs have heights h and 3h , as shown in the figure. Find the value of to omega .
View SolutionA vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.

View SolutionA vertical U-tube contains a liquid of density rho and surface tension T. if the radius of the meniscus of liquid in the limbs of the U-tube are R_(1) and R_(2) find the difference in the liquid column in the limbs.
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
View SolutionA tube of length 'L' is filled completely with an in compressiblem liquid of mass 'M' and closed at both ends. The tube is then rotated in a horizontal plane about one of it's ends with a uniform angular velocity 'ω'. Then which of following statements are true :
View SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionA manometer contains a liquid of density ρ The difference in the levels when the manometer rotates at a constant angular velocity about one of its vertical limbs. (Let 1 be the length of horizontal tube)
View SolutionA U tube is arranged such that diameter of one limb is 2D and diameter of other is D. Surface tension of water contained in the tube is T. If d is density of water, the difference in the levels of liquid is (angle of contact of liquid is zero)
View SolutionA manometer contains a liquid of density ρ. The difference in the levels when the manometer rotates at a constant angular velocity ω about one of its vertical limbs. (Let 1 be the length of horizontal tube)
View SolutionA manometer contains a liquid of density rho . The difference in the levels when the manometer rotates at a constant angular velocity omega about one of its vertical limbs. (Let 1 be the length of horizontal tube)
View Solution
