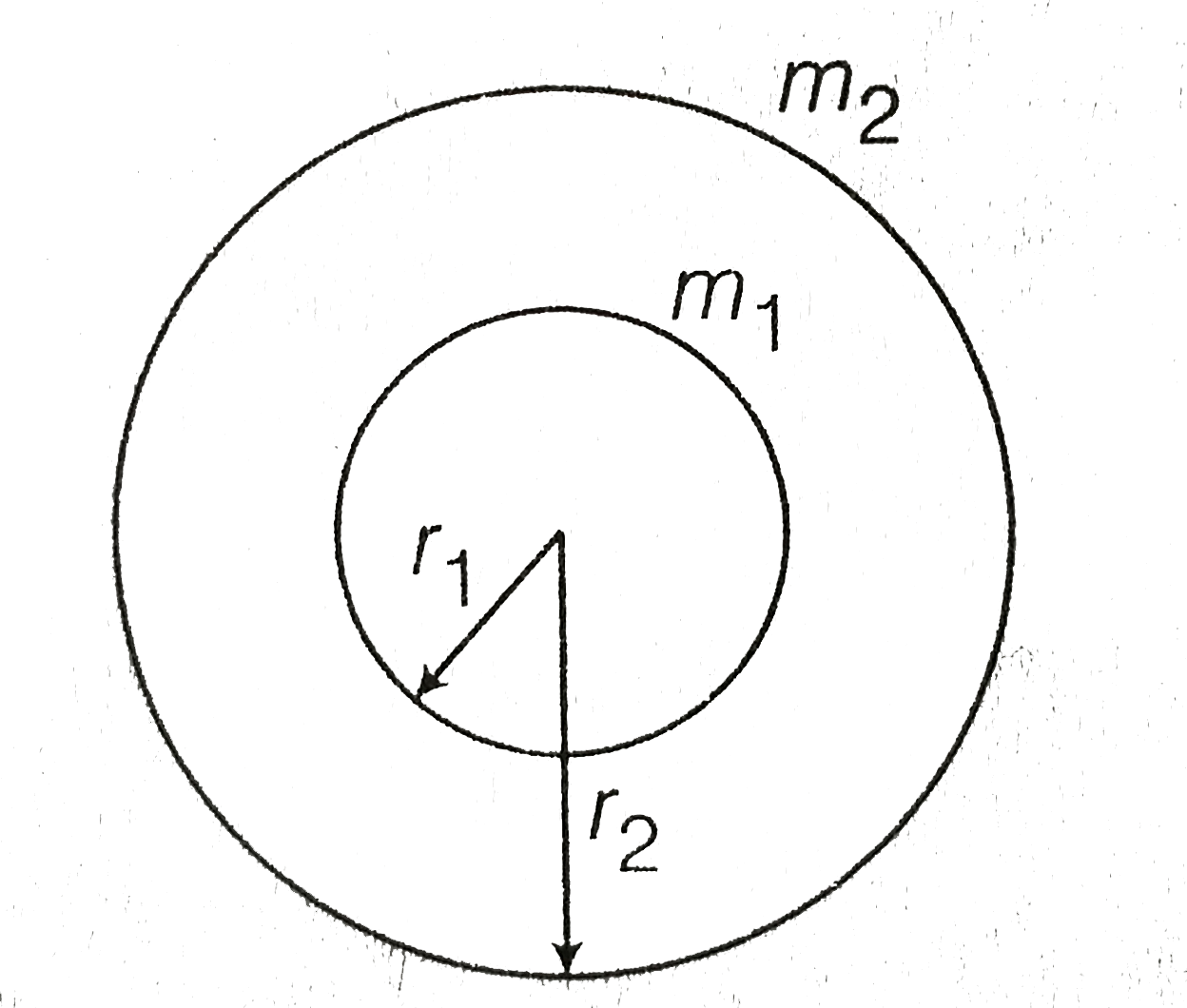
Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?
 Solution in Gujrati
Solution in Gujrati
(a) G(M1+M2)r2, for r<r1
(b) GM1+M2r2 for r<r2
(c) GM2r2 for r1<r<r2
(d) GM1r2 for r1<r<r2
The correct Answer is:D
_E01_031_S01.png)
When r<r1 gravitational intensity is equal to 0
when r>r1 gravitational intensity is equal to GM1r2
When r>r2 gravitational intensity is equal to
G(M1+M2)r2
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 4 A (Conceptual Subjective Exercise)
14 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)
28 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
Statement-1: Two satellites A & B are in the same orbit around the earth B being behind A. B cannot overtake A by increasing its speed.
Statement-2: it will then go into a different orbit.
View Solution_E01_076_Q01.png)
In the given figure L=1 metre if total gravitational force on 4 kg mass is →F1 and on 2 kg mass is →F2 then find out the ratio of ∣∣∣→F1→F2∣∣∣
View SolutionThree identical point mass each of mass 1kg lie in the x-y plane at point (0,0), (0,0.2m) and (0.2m, 0). The net gravitational force on the mass at the origin is
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.
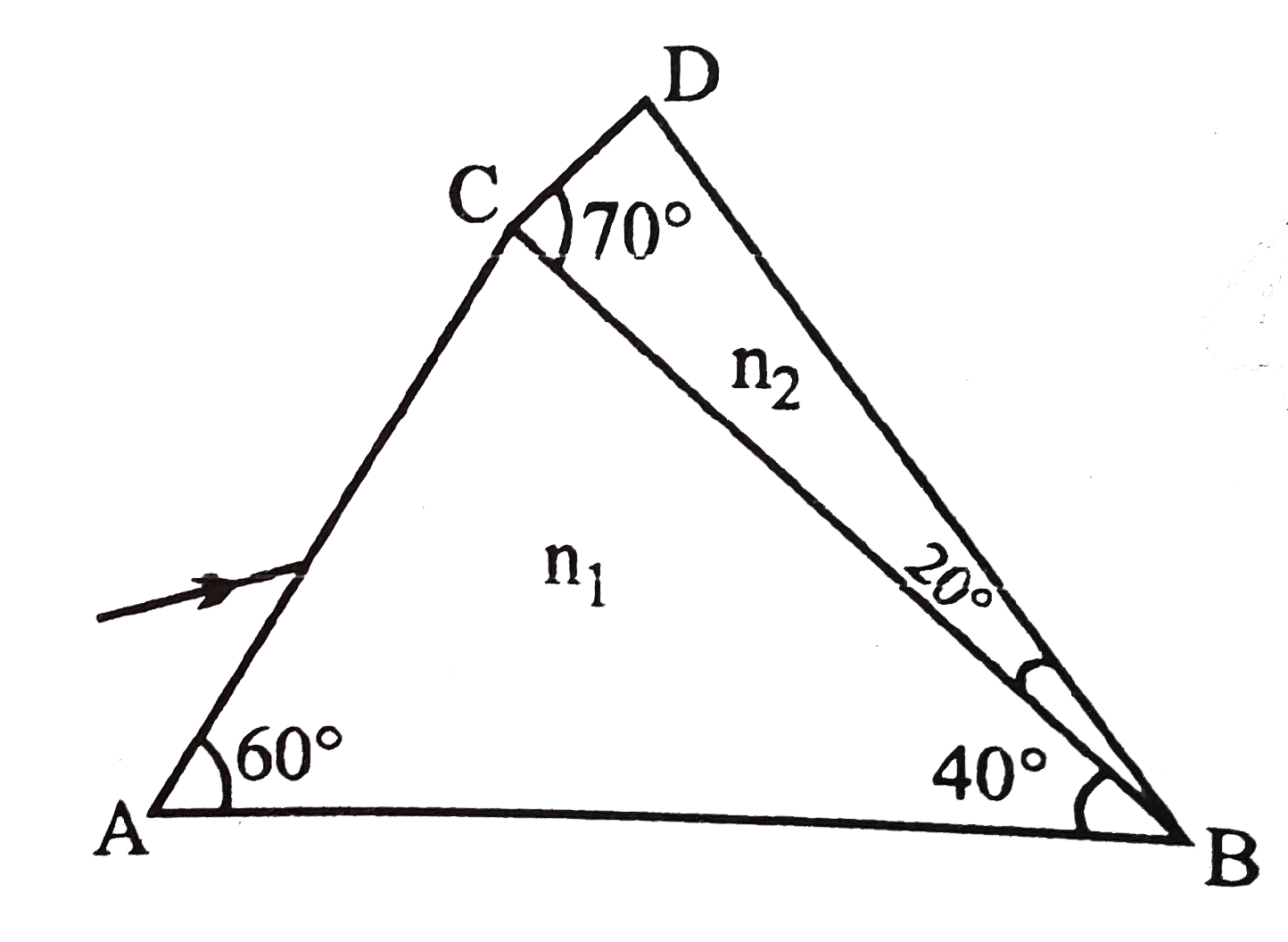
(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionThe figure represents two concentric shells of radii R_(1) and R_(2) and masses M_(1) and M_(2) respectively. The gravitational field intensity at the point A at distance a (R_(1) lt a lt R_(2)) is
View SolutionTwo concentric spherical shells have masses m1, m2 and radit R1,R2(R1<R2). Calculate the force by this system on a particle of mass m, if it is placed at a distance (R1+R2)2 from the centre.
View SolutionTwo concentric spherical shells have masses m_(1) and m_(2) and radii r_(1) and r_(2) (r_(2) gt r_(1)) . What is the force exerted by this system on a particle of mass m_(3) . If it is placed at a distance r(r_(1) lt r lt r_(2)) from the centre ?
View SolutionAssertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionSupposing Newton's law of gravitation for gravitation forces F_(1) and F_(2) between two masses m_(1) and m_(2) at positions r_(1) and r_(2) read where M_(0) is a constant of dimension of mass, r_(12) = r_(1) - r_(2) and n is a number. In such a case,
View SolutionTwo particles of masses m_(1) and m_(2) are moving in concentric circle of radii r_(1) and r_(2) such that their period are same. Then the ratio of their centripetal acceleration is
View SolutionTwo concentric spherical shells of masses and radii m_(1), r_(1) and m_(2), r_(2) respectively are as shown. The gravitational field intensity at point P is
View SolutionSupposing Newton's law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read
where M0 is a constant of dimension of mass, r12=r1−r2 and n is a number. In such a case,
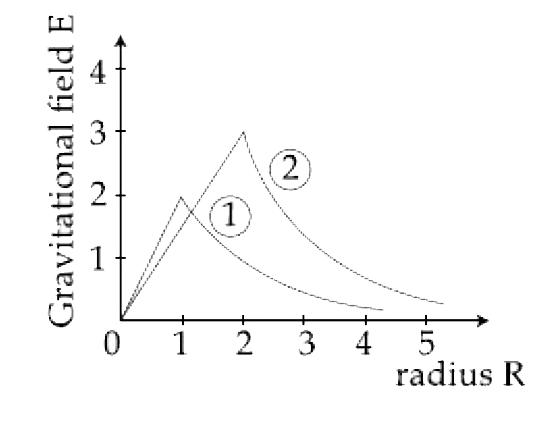
View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
View SolutionTwo concentric spherical shells have masses M1,M2 and radii R1,R2(R1<R2). The force exerted by this system on a particle of mass m. If it is placed at a distance (R1+R22) from the centre.
View SolutionTwo concentric spherical shells have masses M_(1), M_(2) and radii R_(1), R_(2)(R_(1) lt R_(2)) . The force exerted by this system on a particle of mass m. If it is placed at a distance ((R_(1)+R_(2))/(2)) from the centre.
View Solution
