The height at which the acceleration due to gravity becomes g/9 in terms of R. The radius of the earth isSolution in Gujrati
R2
√2R
2R
R√2
The correct Answer is:C
gh=g(1+hR)2=g9⇒(1+hR)2=9
⇒1+hR=3⇒h=2R
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Illustration
34 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 4 B (Brain Storming Subjective Exercise)
20 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo spherical balls of mass 10 kg each are placed 100 m apart. Find the fraviational force of attraction between them.
View SolutionA small satellite revolves around a heavy planet in a circular orbit. At certain point in its orbit a sharp impulse acts on it and instantaneously increases its kinetic energy to 'k' (<2) times without change in its direction of motion show that in its subsequent motion the ratio of its maximum and minimum distance from the planet is k2−k assuming the mass of the satellite is negligibly small as compared to that of the planet.
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.
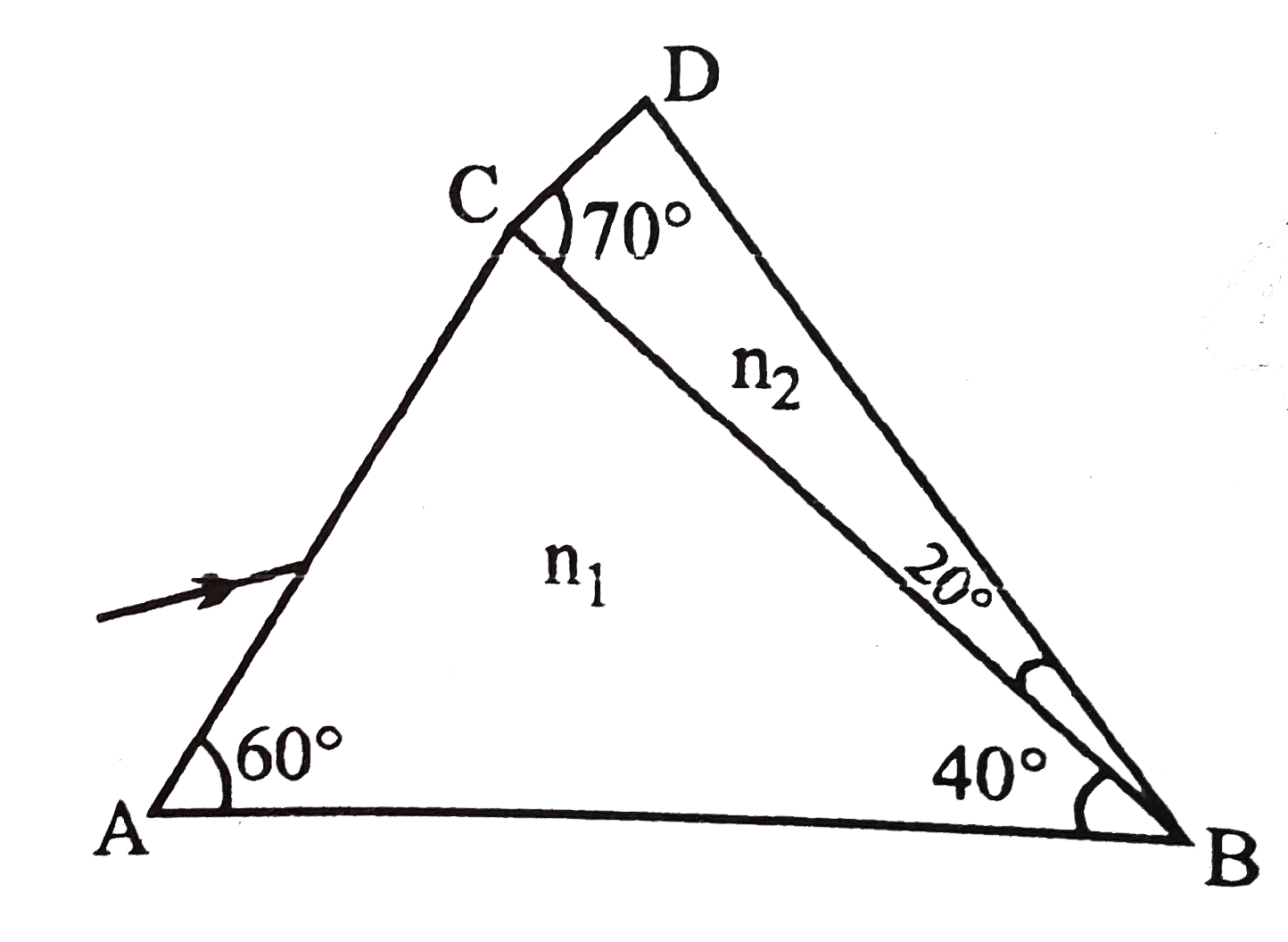
(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionThe height at which the acceleration due to gravity becomes (g)/(9) (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionIf g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
View SolutionWhat will be the acceleration due to gravity at height h if h gt gt R . Where R is radius of earth and g is acceleration due to gravity on the surface of earth
View SolutionThe height at which the acceleration due to gravity becomes g//9 in terms of R the radius of the earth is
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth is
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g = the acceleration due to gravity on the surface of the Earth) in terms of R, the radius of the Earth, is:
View SolutionThe height at which the acceleration due to gravity becomes (g)/(9) (where g = the acceleration due to gravity on the surface of the Earth) in terms of R, the radius of the Earth, is:
View SolutionIf R is the radius of the Earth and g is the acceleration due to gravity on the Earth's surface. Find the mean density of the Earth.
View SolutionThe height at which the acceleration due to gravity becomes g/9 (where g = acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth is .........
View SolutionThe height at which the acceleration due to gravity becomes g9 (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionIf R is the radius of the earth and .g. the acceleration due to gravity, the mass of the earth is
View Solution
