_E01_104_Q01.png)
Two plane mirrors, a source S of light, emitting monochromatic rays of wavelength λ and a screen are arranged as shown in figure. If angle θ is very small, calculate fringe width of the interference pattern formed by reflected rays.Solution in Gujrati
The correct Answer is:2(a+b)λ4aθ
_E01_104_S01.png)
Distance between two sources S1 and S2 d=2×2acosθsinθ=2asin2θ
Screen distance D=b+2acos2θ
β=λDd=λ(b+2acos2θ)2asin2θ=λ(b+2a)4aθ
(if θ is very much small)
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)17videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 5 B (Previous Years Questions)19videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 4 A (Conceptual subjective Exercise)9videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
To demonstrate the phenomenon of interference, we require two sources which emit radiation ......
06:46View SolutionTwo beams of ligth having intensities I and 4I interface to produce a fringe pattern on a screen. The phase difference between the beams is π2 at point A and π at point B. Then the difference between the resultant intensities at A and B is
11:31View SolutionConsider interference between two sources of intensity I and 4I. Find out resultant intensity where phase difference is (i). π/4
(ii). π
(iii). 4π04:25View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :
09:02View SolutionIn Lloyd's mirror experiment (Fig.) a light wave emitted directly be the source S (narrow slit) interferes with the wave reflected form a mirror M. As s result, an interference fringe pattern is
formed on the screen Sc. the source and the mirror are separated by a distance l=100cm.At a certain position of the source the fringe width on the screen was equal to Δx=0.25mm, and after source was moved away from the mirror plane by Δh=0.60mm, the fringe width decreased η=1.5 times. Find the wavelength of light.05:51View SolutionThe arrangement for a mirror experiment is shown in figure. S is a point source of frequency 6xx10^(14)Hz . D and C represent the two ends of a mirror placed horizontally and LOM represents the screen. Find the fringe width of the fringe pattern ?
View Solution-
Two plane mirrors, a source S of light, wmitting monochromatic rays of wavelength λ and a screen are arranged as shown in figure. If angle θ is very small, calculate fringe width of the interference pattern formed by reflected rays.01:16View Solution Two plane mirrors, a source S of light, emitting wavelengths of lambda_(1) = 4000overset(@)A" and" lambda_(2) = 5600overset(@)A and a screen are arranged as shown in figure. The angle theta shown is 0.05 radian and distance a and b are 1 cm and 38 cm respectively. (a) Find the fringe width of interference pattern formed on screen by the blue light. (b) Calculate the distance of first black line from central bright fringe. (c) Find the distance between two black lines which are nearest to the central bright fringe.
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
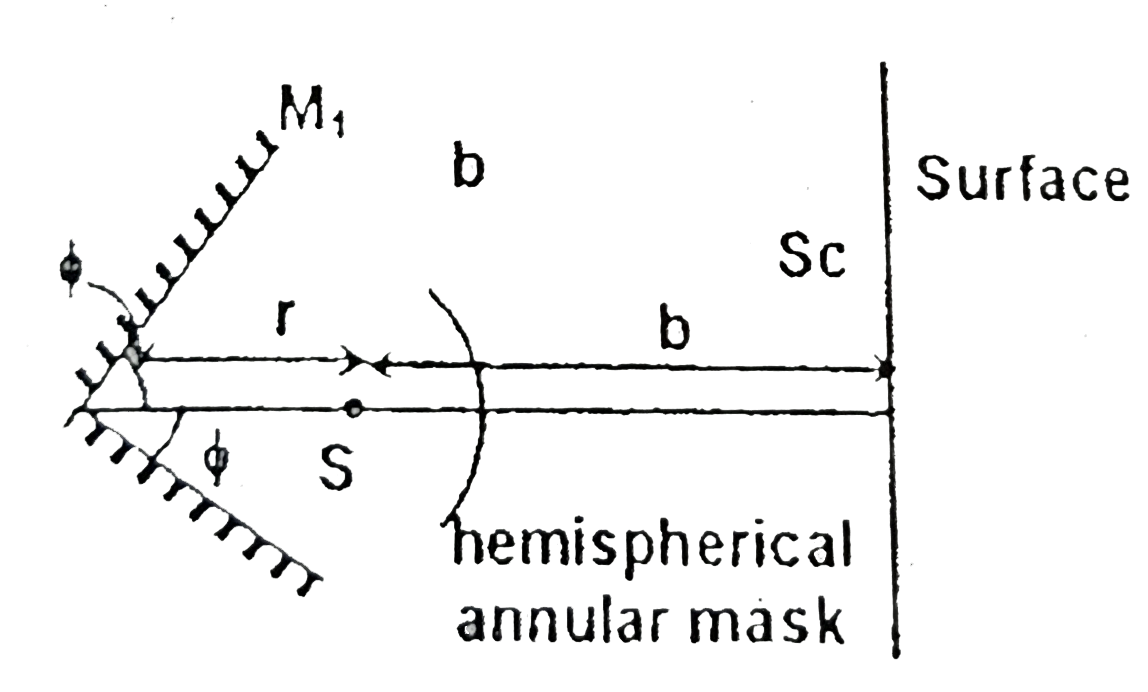01:47View SolutionA prism having angle A∘ (which is very small) is placed in front of a point source S at a small distance d. A screen is placed at a large distance D as shown in the figure-6.113. Find the fringe width of interference pattern given that source is emitting light of wavelength λ and refractive index of prism is μ.
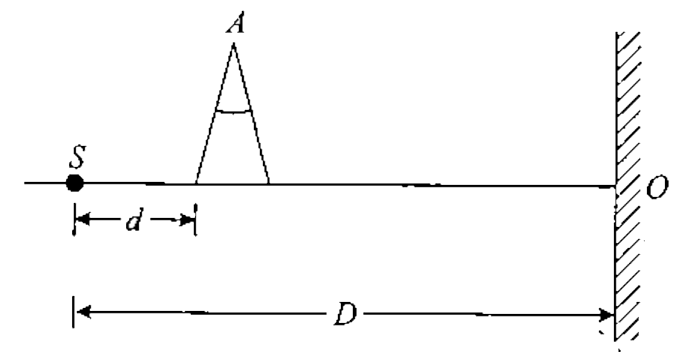03:19View SolutionA mirror is inclined at an angle of theta with the horizontal. If a ray light is incident at an angle theta as shown , then the angle made by reflected ray with the horizontal is
04:19View SolutionThere are two plane mirrors. They are mutually inclined as shown in figure. S is a source of monochromatic light of wavelength λ. The reflected beam interfere and fringe pattern is obtained on the screen. If θ is small, the fringe width will be :
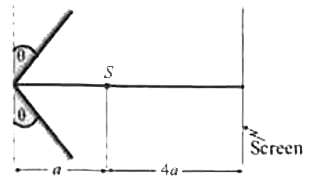04:34View SolutionAssertion: A monochromatic source of light is placed above a plane mirror as shown in figure. Fringes will be obtained at all points above O but not below it on the screen. Reason: All reflected rays will suffer a phase difference of pi .
02:15View SolutionA mirror is inclined at an angle of θ with the horizontal. If a ray light is incident at an angle θ as shown , then the angle made by reflected ray with the horizontal is
_E01_002_Q01.png)
08:15View SolutionA slit illuminated by monochromatic light is held 0.4 mm from the surface of a plane mirror. The fringe width in the interference pattern obtained with reflected and direct light is 0.25 mm. The screen is at 50 cm from the slit. The wavelength of light is
04:57View Solution