In figure S is a monochromatic point source emitting light of wavelength . A thin lens of circular shape and focal length is cut into two identical halves and by a plane passing through a diameter. The two halves are placed symmetrically about the central axis with a gap of . The distance along the axis from to and is , while that from and to is . The screen at is normal to .
(a) If the intensity maximum occurs at point on screen, find distance .
(b) If the gap between and is reduced from its original value of , will the distance increases, decreases or remain the same?
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:(i). 1 mm
(ii). Increases
(i). For the lens
therefore using we have
or
Linear magnitfication ltbr> Hence two images and of S will be formed at 0.3m from the lens as shown in figure. Image due to part 1 will be formed at 0.5 mm above its optic axis (m=-2). Similarly, due to part 2 is formed 0.5 mm below the optic axis of this part as shown.
Hence distance between and
Therefore, fringe width,
now, as the point A is at the third maxima
or
(ii). if the gap between and is reduced, d will decrease. Hence, the fringe width will increase or distance OA will increase
_E01_105_S01.png)
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)17videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 5 B (Previous Years Questions)19videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 4 A (Conceptual subjective Exercise)9videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
To demonstrate the phenomenon of interference, we require two sources which emit radiation ......
03:50View SolutionTwo beams of ligth having intensities I and 4I interface to produce a fringe pattern on a screen. The phase difference between the beams is π2 at point A and π at point B. Then the difference between the resultant intensities at A and B is
14:09View SolutionConsider interference between two sources of intensity I and 4I. Find out resultant intensity where phase difference is (i). π/4
(ii). π
(iii). 4π02:23View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :
 05:20View Solution
05:20View SolutionIn the xy plane,the line L_(1) passes through the point (1,1) and the line L_(2) passes through the point (-1,1). If the difference of the slopes of the lines is 2. Then the locus of the point of intersection of the lines L_(1) and L_(2) is
04:45View SolutionLet L_(1) be the projection and L_(2) be the image of the Z-axis in the plane 3x-4y+z+1=0 then find the distance of the point (4,3,5) from the plane containing the lines L_(1) and L_(2)
02:38View SolutionTwo separated sources emit sinusoidal travelling waves but have the same wavelength lambda and are in phase at their respective sources . One travels a distance l_(1) to get to the observeration point while the other travels a distance l_(2) . The amplitude is minimum at the observation point , l_(1) - l_(2) is an
12:38View SolutionTwo identical concex lenses L_(1) and L_(2) are placed at a distance of 20cm from each other on the common principal axis .The focal length of each lens is 15cm and the lens L_(2) is to the right of lens A .A point object is placed at a distance of 20cm on the left on lens L_(1) on the common axis of two lenses.Find where a convex mirror of radius of curvature 5cm should be placed so that the final image coincides with the object.?
03:15View SolutionIn figure S is a monochromatic point source emitting light of wavelength lambda=500 nm . A thin lens of circular shape and focal length 0.10 m is cut into two identical halves L_(1) and L_(2) by a plane passing through a doameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm . The distance along the axis from A to L_(1) and L_(2) is 0.15 m , while that from L_(1) and L_(2) to O is 1.30 m . The screen at O is normal to SO . (a) If the 3^(rd) intensity maximum occurs at point P on screen, find distance OP . (b) If the gap between L_(1) and L_(2) is reduced from its original value of 0.5 mm , will the distance OP increases, devreases or remain the same?
04:56View SolutionIn the figure shown, there are two convex lenses L_(1) and L_(2) having focal. Lengths f_(1) and f_(2) respectively. The distance between L_(1) and L_(2) will be
View Solutionसंलग्न चित्र में S एकवर्णीय बिंदु - स्रोत है जो λ=500 नैनोमीटर तरंगदैर्ध्य का प्रकाश उत्सर्जित कर रहा है | वृत्ताकार आकार का एक पतला लेंस जिसकी फोकस दूरी 0.10 मी है, एक व्यास में से गुजरने वाले तल के द्वारा दो समरूप अर्द्ध - भागों L1 व L2 में काटा गया है | ये दो अर्द्ध - भाग केंद्रीय अक्ष SO के सापेक्ष 0.5 मिमी के अंतराल पर सममित रूप से रखे गए हैं | अक्ष के अनुदिश S से L1 व L2 की दूरी 0.15 मी है तथा L1 व L2 से की दूरी 1.30 मी है | O पर रखा पर्दा, SO के लम्बवत है |
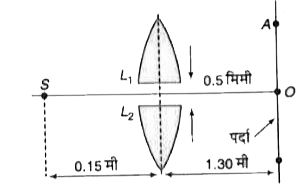
यदि तीसरा तीव्रता उच्चिष्ठ पर्दे पर बिंदु a पर हो तो दूरी OA ज्ञात कीजिए |
(b) यदि L1 व L2 के बीच अंतराल मूल मान 0.5 मिमी से घटा दिया जाए, तो क्या दूरी OA बढ़ेगी, घटेगी अथवा वही रहेगी ?06:40View SolutionThe distance between two points P and Q is d and the lengths of projections of PQ on the coordinate planes are l1,l2,l3 then l1+l22+l23d2
03:45View SolutionIn the following ray diagram the positions of an object O, image I and two lenses L_(1) and L_(2) and a mirror M are given. The focal length of L_(1) is 10 cm. Find the focal length of L_(2) .
01:26View SolutionS is a monochromatic point source emitting light of wavelength l = 500 nm. A thin lens of circular shape and of focal length 0.10 m is cut into two identical halves L1 and L2 by a plane passing through a diameter. The two halves are placed symmetrically about the central axis SO with a gap of 0.5 mm. The distance along the axis from S to L1 and L2 is 0.15 m, while that from L1 and L2 to O is 1.30 m. The screen at O is normal to SO. If the third intensity maximum occurs at point A on the screen, find the distance OA.
07:51View SolutionIn the image shown, 'S' is a monochromatic point source emitting light of 500 nm wavelength. Circular shape and a thin superfluous lens of 0.10m focus distance two identical halves L_1 and L_2 Is cut from a plane passing through Vyasa. Both parts are symmetrically placed at the 0.5 mm interval of the central axis SO. S_1 From L_1 and L_2 The distance along the axis of K is 0.15 m while L_1 and L_2 The distance from O to 1.30 m. The curtain at 0 is reflective of SO. If A is found at point A on the third superlative screen, find the distance OA.
01:49View Solution

