A Young's double slit interference arrangement with slits S1 and S2 is immersed in water (refractive index =4/3) as shown in the figure. The positions of maxima on the surface of water are given by x2=p2m2λ2−d2, where λ is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:3
_E01_143_S01.png)
x1=√x2+d2
x2=43√x2+d2
Δx=(43−1)√x2+d2=nλ
13√x2+d2=nλ
(x2+d2)=9n2λ2
∴(P=3)
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)7videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)17videos
WAVE OPTICS
- BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Electromagnetic waves are transverse is nature is evident by
01:53View SolutionTo demonstrate the phenomenon of interference, we require two sources which emit radiation ......
10:46View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :
 02:02View Solution
02:02View SolutionDetermine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is lambda/(2(mu-1)) , where lambda is the wavelength of the incident light and mu is the index of refraction of the film.
02:46View SolutionIn figure S is a monochromatic source of light emitting light of wavelength of wavelength lambda (in air). Light on slits S_(1) from S and then reaches in the slit S_(2) and S_(3) through a medium of refractive index mu_(1) . Light from slit S_(2) and S_(3) reaches the screen through a medium of refractive index mu_(3) . A thin transparent film of refractive index mu_(2) and thickness t is used placed in front of S_(2) . Point P is symmetrical w.r.t. S_(2) and S_(3) . Using the values d = 1 mm, D = 1 m, mu_(1) = 4//3 , mu_(2) = 3//2, mu_(3) = 9//5 , and t = (4)/(9) xx 10^(-5) m , a. find distance of central maxima from P, b. If the film in front of S_(2) is removed, then by what distance and in which direction will be central maxima shift ? .
02:42View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
01:47View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be (assume θ to be a small angle)
View SolutionIn Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,where I0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)
 04:30View Solution
04:30View SolutionIn a Young's double slit experiment, let S_(1) and S_(2) be the two slits, and C be the centre of the screen. If angle S_(1)CS_(2)=theta and lambda is the wavelength, the fringe width will be
View SolutionColumn I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits S1 and S2 . In each of these cases S1P0=S2P0,S1P1−S2P1=λ/4 and S1P2−S2P2=λ/3, where λ is the wavelength of the light used. In the cases B,C and D, a transparent sheet of refractive index μ and thickness t is pasted on slit S1 . The thicknesses of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by δ(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation.
04:30View Solutionएक यंग द्विझिरी व्यतिकरण सेट - अप, जिसकी झिरियाँ तथा हैं को दर्शाए चित्रानुसार पानी ( अपवर्तनांक = 4/3 ) में डुबाया गया है | पानी की सतह पर महत्तम तीव्रता की स्थितियाँ x2=p2m2λ2−d2 सम्बन्ध द्वारा दी जाती हैं | यहाँ पर λ प्रकाश की वायु ( अपवर्तनांक = 1 ) में तरंगदैर्ध्य, 2d झिरियों के मध्य दूरी तथा m एक पूर्णांक है | तब, P का मान है
 View Solution
View SolutionIn a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is lambda .The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2.Choose the correct choice(s).
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then the fringe width for the light of wavelength λ will be (assume θ to be a small angle)
View SolutionConsider the arrangement shown in figure, By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P which is at the common perpendicular bisector of S1S2 and S3S4. When z=Dλ2d, the intensity measured at P is I. Find this intensity when z is equal to 1) Dλd, (2) 3Dλ2d and (3) 2Dλd.
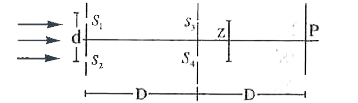 05:19View Solution
05:19View SolutionLight of wavelength lambda = 500 nm falls on two narrow slits placed a distance d = 50 xx 10^(-4) cm apart, at an angle phi = 30^(@) relative to the slits shown in figure. In front of the lower slit, a slab of thickness 0.1 mmand refractive index 3/2 is placed. The interference pattern is observed on a screen at a distance D = 2m from the slits S_(1)O = S_(2)O = d//2 The position of central maxima is at an angular position 'theta' with line OB
03:17View SolutionIn Young's double slit experiment the point source is placed slightly off the central axis as shown in figure. The plane of slits (S1,S2) and screen are separated by a distance of 2m. The separation between the slits is 10 mm. The position of the slit above the axis is 1mm. if the wavelength λ=4000Å in the above arrangement

If central maximum is to occur at point 'P' then a sheet of thin film of refractive index μ=1.5 can be introduced in the path of rays from one the slits to the point 'P'. (t-thickness of film)03:39View Solution

