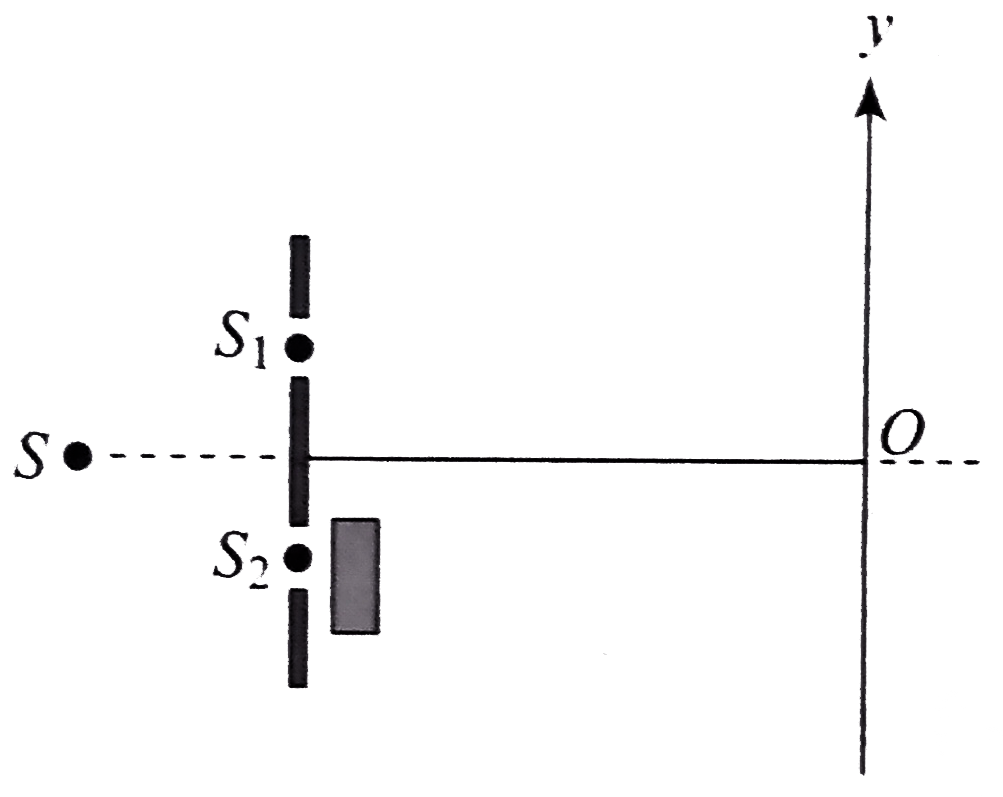
The young's double slit experiment is done in a medium of refractive index 4/3.A light of 600nmwavelength is falling on the slits having 0.45 mm separation .The lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index1.5.the intereference pattern is observed ona screen placed 1.5m from the slits are shown
![The young's double slit experiment is done in a medium of refractive index 4//3.A light of 600nmwavelength is falling on the slits having 0.45 mm separation .The lower slit S(2) is covered by a thin glass sheet of thickness 10.4mu m and refractive index1.5.the intereference pattern is observed ona screen placed 1.5m from the slits are shown (a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis. (b) Find the light intensity at point Orelative to the maximum fringe intensity. (c )Now,if 600nmlight is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O.[All wavelengths in this problem are for the given medium of refractive index 4//3 .Ignore dispersion]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_WO_C02_E01_008_Q01.png)
(a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis.
(b) Find the light intensity at point Orelative to the maximum fringe intensity.
(c )Now,if 600nmlight is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O.[All wavelengths in this problem are for the given medium of refractive index 4/3 .Ignore dispersion]Solution in Gujrati
The correct Answer is:(i). 4.33m
(ii). I=3Imax4
(iii). 650nm;433.33 nm
_E01_138_S01.png)
(i) location of central maximum on y-axis let the central maximum be obtained at a distance y below point O. it will be below O because glass sheet covers the lower slit.
Δx1=S1P−S2P=ydD
Due to glass sheet Δx2=(μgμm−1)t
For zero path difference Δx1=Δx2
⇒ydB=(μgμm−1)t⇒y=(μgμm−1)tDd
⇒y=(3/24/3−1)(10.4×10−60.45×10−3)(1.5)
y=4.33×10−3m=4.33mm
(ii) Light intensity at O, Δx1=0,Δx2=(μgμm−1)t
∴ Net phase difference =2πyΔx2
∴ϕ=2π6×10−7(3/24/3−1)(10.4×106)=13π3
∴I(ϕ)=Imaxcos2(ϕ2) or I(ϕ)Imax=34=0.75
(iii). Wavelength of light that form maxima O. if 600 nm light is replaced by 400 to 700 nm light
At O,Δx=(μgμm−1)t
For maximum intensity at O, Δx=nλ
where n=1,2,3...
∴λ=Δx1,Δx2,Δx3
Δx=(3/24/3−1)(10.4×10−6m) or Δx=1300nm
For maximum intensity at O,
λ=1300nm,13002nm,13002nm,13004nm
λ=1300nm,650nm,433.33nm ....
or λ=6.5×10−7m,4.33×10−7m
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)
17 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Electromagnetic waves are transverse is nature is evident by
View SolutionTo demonstrate the phenomenon of interference, we require two sources which emit radiation ......
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionA YDSE is performed in a medium of refractive index 4 // 3 , A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S_(2) is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4 // 3 , ignore absorption.) Find the light intensity at point O relative t maximum fringe intensity.
View SolutionA YDSE is performed in a medium of refractive index 4 // 3 , A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S_(2) is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4 // 3 , ignore absorption.) Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.
View SolutionThe young's double slit experiment is done in a medium of refractive index 4//3 .A light of 600nm wavelength is falling on the slits having 0.45 mm separation .The lower slit S_(2) is covered by a thin glass sheet of thickness 10.4mu m and refractive index 1.5 .the intereference pattern is observed ona screen placed 1.5m from the slits are shown (a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis. (b) Find the light intensity at point O relative to the maximum fringe intensity. (c )Now,if 600nm light is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O .[All wavelengths in this problem are for the given medium of refractive index 4//3 .Ignore dispersion]
View SolutionThe young's slit experiment is done in a medium of refractive index 4//3 .A light of 600 nm wavelength is falling on the slits having 0.45 mm separation . The lower slit S_(2) is covered by a thin galss sheet of thickness 10.4 mum and r3efractive index 1.5 .The interferecnce pattern is observed on a screen placed 1.5 m form the slits as shown in figure .Find the light intensity at point O relative to the maximum fringle intensity (Given : cos3.4 =sqrt(0.75)
View SolutionYoung’s double slit experiment is done in a medium of refractive index 4/3. Light of 600 nm wavelength is falling on the slits having 0.45 pm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 pm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown. (a) Find the location of central maxima (bright fringe with zero I t y path difference) on the y-axis. (b) Find the light intensity at point O relative to the maximum fringe intensity. (c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that from maxima exactly at point O[All wavelengths in this problem are for the given medium of refractive index 4/3 . Ignore dispersions.]
View SolutionIn Young's double slit experiment the point source is placed slightly off the central axis as shown in figure. The plane of slits (S1,S2) and screen are separated by a distance of 2m. The separation between the slits is 10 mm. The position of the slit above the axis is 1mm. if the wavelength λ=4000Å in the above arrangement

If central maximum is to occur at point 'P' then a sheet of thin film of refractive index μ=1.5 can be introduced in the path of rays from one the slits to the point 'P'. (t-thickness of film)
View SolutionThe young's double slit experiment is done in a medium of refractive index 4/3 . A light of 600 nm wavelength is falling on the slits having 0.45 mm separation. The lower slit S_(2) is covered by a thin glass sheet of thickness 10.4 mu m and refractive index 1.5. The interference pattern is observed on a screen placed. 1.5 m from the slit as shown in figure. Find the light intensity at point O relative to the maximum fringe intensity
View SolutionThe Young.s double slit experiment is done in a medium of refractive index 4/3 . A light of 600 nm wavelength is falling on the slits having 0.45 mm separation . The lower slit S_(2) is covered by a thin glass sheet of thickness 10.4 mu m and refractive index 1.5 . The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure .Find the light intensity at point O relative to the maxmum fringe intensity
View SolutionYoung bi-slit experiments are performed in a medium with a 4/3 refractive index. 600nm wavelength light is incident on 0.45 mm gap slits. 10.4 mu The lower slit S is covered by a thin glass plate of m thickness and 1.5 refractive index. The articulation format is observed diagrammatically on a screen 1.5m from the slito. Find the position of the central superlative (bright fridge with zero transition) on the y-axis.
View SolutionYoung bi-slit experiments are performed in a medium with a 4/3 refractive index. 600nm wavelength light is incident on 0.45 mm gap slits. 10.4 mu The lower slit S is covered by a thin glass plate of m thickness and 1.5 refractive index. The articulation format is observed diagrammatically on a screen 1.5m from the slito. Find the intensity of light at a point O compared to the maximum fridge intensity.
View SolutionYoung bi-slit experiments are performed in a medium with a 4/3 refractive index. 600nm wavelength light is incident on 0.45 mm gap slits. 10.4 mu The lower slit S is covered by a thin glass plate of m thickness and 1.5 refractive index. The articulation format is observed diagrammatically on a screen 1.5m from the slito. Now, if 600 nm light is displaced by white light of 400 to 700 nm range, then light. Find the wavelength which is at the point 0 as the altitude. [In this problem, all wavelengths are for a given medium of 4/3 refractive index. Deflection is ignored.]
View SolutionThe Young's double-slit experiment is done in a medium of refractive index 4/3. A light of 600 nm wavelength isfalling on the slits having 0.45 mm separation. The lower shift S2 is covered by a thin glass sheet of refractive index. 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in Figure
a. Find the location of central maximum (bright fringe with zero path difference) on the y-axis.
b. Find the light intensity of point O relative to the maximum fringe intensity.
c. Now , if 600 nm light is replaced by white light of range 400 - 700 nm, find the wavelengths of the light that from maxima exaclty at point O.
(All wavelength in the problem are for the given medium of refractive index 4/3 Ignoe dispersion.)

View Solution
