A Rubber Ball Rebound
A rubber ball of mass 2.0kg falls to the floor. The ball hits with a speed of 8m/s and rebounds with approximately the same speed. High speed photographs show that the ball is in contact with the floor for 10^-3s. What can we say about the force exerted on the ball by the floor?Solution in Gujrati
The momentum of the ball just before it hits the floor is Pa=1.6ˆkkg−m/s and its momentum 10−3 later is Pb=+1.6ˆkkg−m/s
Since tb∫taFdt=Pb−Pa
tb∫taFdt=1.6ˆk−(−1.6ˆk)=3.2ˆkkg−m/s
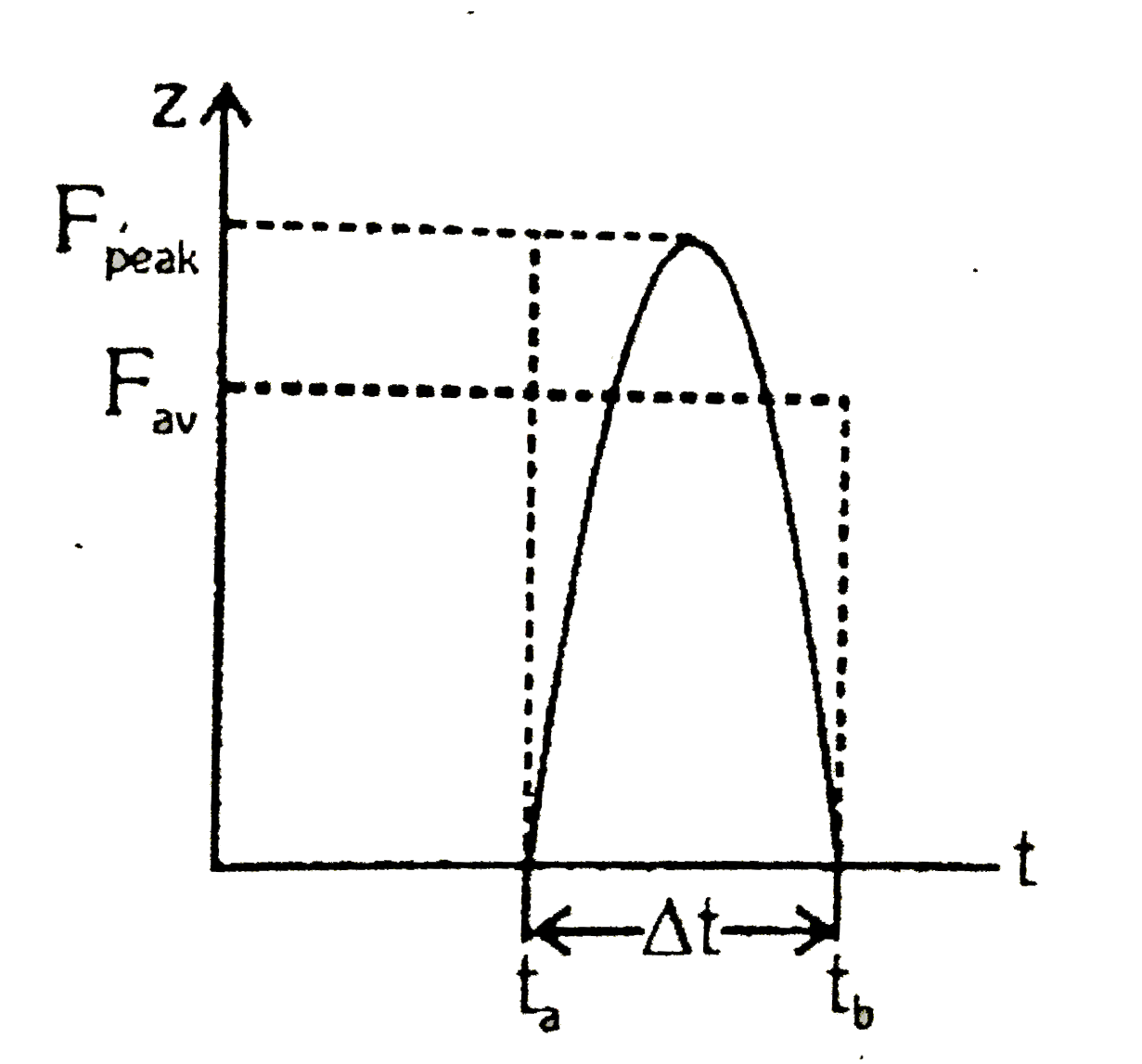
Although the exact variation of F with time is not known, it is easy to find the average force exerted by the floor on the ball. IF the collision time is Δt=tb−ta, the average force Fav acting during the collision is
FavΔt∫ta+ΔttaFdt
Since Δt=10−3s,
Fav=3.2ˆkkg−ms10−2s=3200ˆkN
The average force is directed upward, as we expect. In more familiar units, 3200N=720lb−−a sizable force. The instantanwous force on the ball is even larger at the peak, as the sketch shows. If the ball hits a resillient surface, the collision time is longer and the peak force is less.
Actually, there is a weakness in our treatment of the rubber ball rebound. In calculating the impulse ∫Fdt,F is the total force. this includes the gravitational force, which we have neglected. Proceeding more carefully, we write.
F=Ffloor+Fgrav=Ffloor−Mgˆk.
The impulse equation then becomes
∫10−30Ffloordt−∫10−30Mgˆkdt=3.2ˆkkg−m/s The impulse due to the gravitational force is −∫10−30Mgˆkdt=−Mgˆk∫10−30dt=(0.2)(9.8)(10−3)ˆk=−1.96×10−3ˆkkg−m/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
The centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
View SolutionTwo particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA ball weighing 10g hits a hard surface vertically with a speed of 5m//s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
View SolutionA ball of 1 kg drops vetically on to the floor with a speed of 25ms−1 . It rebounds with an initial velocity of 10ms−1 . (a) What impulse acts on the ball during contact ? (b) If the ball is in contact for 0.02 s , what is the average force exerted on the floor ?
View SolutionA ball weighing 10g hits a hard surface vertically with a speed of 5m/s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
View SolutionA 1.5 kg ball drops vertically on a floor hitting with a speed of 25 ms1. It rebounds with an initial speed of 15ms−1. If the ball was in contact for only 0.03, the force exerted on the floor by the ball is
View SolutionA rubber ball of mass 0 *4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0*4 s, find the average force exerted by the ball on the ground .
View SolutionA metal ball hits a wall and does not rebound whereas a rubber ball of the same mass on hitting the wall the same velocity rebounds back. It can be concluded that–
View SolutionA ball of mass 10 gm dropped from a height of 5m hits the floor and rebounds to a height of 1.25m. If the ball is in contact with the ground for 0.1s, the force exerted by the ground on the ball is (g=10 m//s^(2))
View SolutionA ball weighing 10 gm hits a hard surface vertically with a speed of 5 m//s and rebounds with the same speed. The ball remains in contact with the surface for 0.01 sec. The average force exerted by the surface on the ball is :
View SolutionA metal ball hits a wall and does not rebound, where as b a rubber ball of the same mass on hitting the wall with the same velocity rebounds back. It can be concluded that:
View SolutionA metal ball hits a wall and does not rebound, where as a rubber ball of the same mass on hitting the wall with the same velocity rebounds back. It can be concluded that:
View SolutionA ball weighing 50g hits a hard surface normally with a speed of 25m/s and rebounds with the same speed. The ball remains in contact with the surface for 0.05s .The average force exerted by the surface on the ball is?
View SolutionA ball of mass 10 gm dropped from a height of 5 m hits the floor and rebounds to a height of 1.25 m. If the ball is in contact with the ground for 0.1s, the force exerted by the ground on the ball is (g = 10 m/s2)
View Solution
