Two particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct. Solution in Gujrati
→vA+→vB=0
mA→vA+mB→vB=0
WA+WB=0
→aA+→aB=0
The correct Answer is:B
In the absence of external forces, the linear momentum of the system remains constant.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
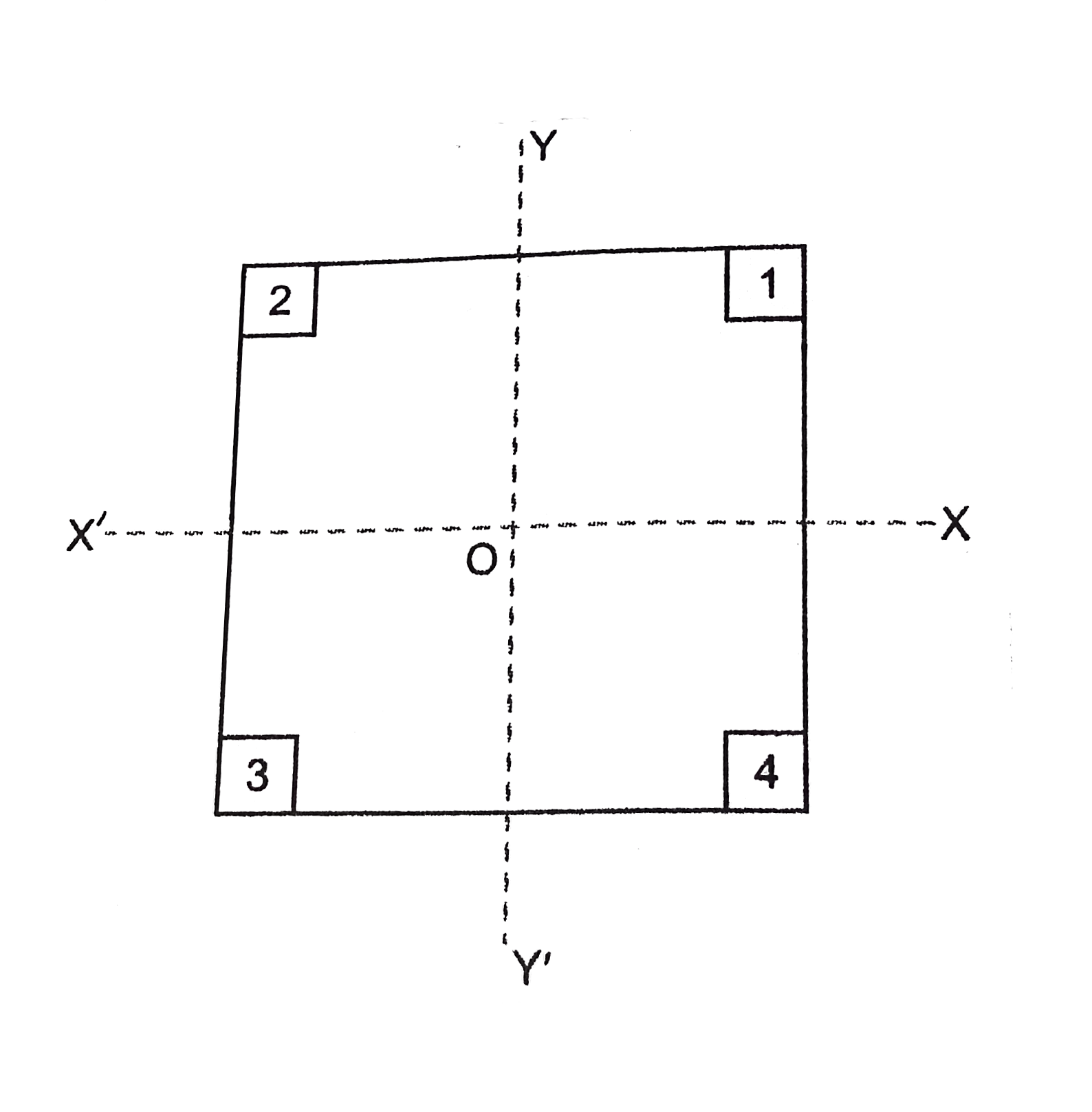
View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionThe centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionTwo particles of masses m_(1) and m_(2) in projectile motion have velocities vec(v)_(1) and vec(v)_(2) , respectively , at time t = 0 . They collide at time t_(0) . Their velocities become vec(v')_(1) and vec(v')_(2) at time 2 t_(0) while still moving in air. The value of |(m_(1) vec(v')_(1) + m_(2) vec(v')_(2)) - (m_(1) vec(v)_(1) + m_(2) vec(v)_(2))|
View SolutionTwo particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionThe velocity of a particle varies with time as per the law →v=→a+→b t where →a and →b are two constant vectors. The time at which velocity of the particle at t=0 is :
View SolutionTwo vectors →A and →B have magnitudes 2 and 2√2 respectively. It is found that →A.→B=∣∣→A×→B∣∣, then the value of ∣∣ ∣∣→A+→B→A−→B∣∣ ∣∣ will be :
View Solutionदो वेक्टर →A व →B के लिए सिद्ध कीजिये कि यदि ∣∣→A+→B∣∣=∣∣→A−→B∣∣ हो तो →A व →Bपरस्पर लंबवत है ।
View Solutionदो परस्पर लम्बवत वेक्टरो →A तथा →B के परिमाण क्रमशः 6 तथा 8 है एक नामांकित आरेख बनाकर →A−→B का परिमाण तथा दिशा ज्ञात कीजिये
View SolutionConsider the following inequalities in respect of vectors →aand→b:
1. |vec(a)+vec(b)| £|vec(a)|+|vec(b)|
2. ∣∣→a−→b∣∣3|→a|−∣∣→b∣∣
Which of the above is/are correct ?
View SolutionIf →a,→b,→c are mutually perpendicular vectors having magnitudes 1,2,3 respectively, then [→a+→b+→c →b−→a→c]=
View SolutionA particle is moving along a circular path. The angular velocity, linear velocity, angular acceleration and centripetal acceleration of the particle at any instant are →ω,→v,→a,→ac respectively. Which of the following relations are correct ?
View SolutionTwo bodies A and B are moving with velocities vec(V)_(A) and vec(V)_(B) making an 'theta' with each other. Determine the relative velocity of A with respect to B. What will be the relative velocity . When two bodies are moving in the same direction.
View Solution
