As shown, a big box of mass M is resting on a horziontal smooth florr. On the bottom of the box there is a small block of mass m. The block is given an intial speed v0 relative to the floor, and starts to bounce back and forth between the two walls of the box. Find the final speed of the box when the block has finally come to rest in the box :-
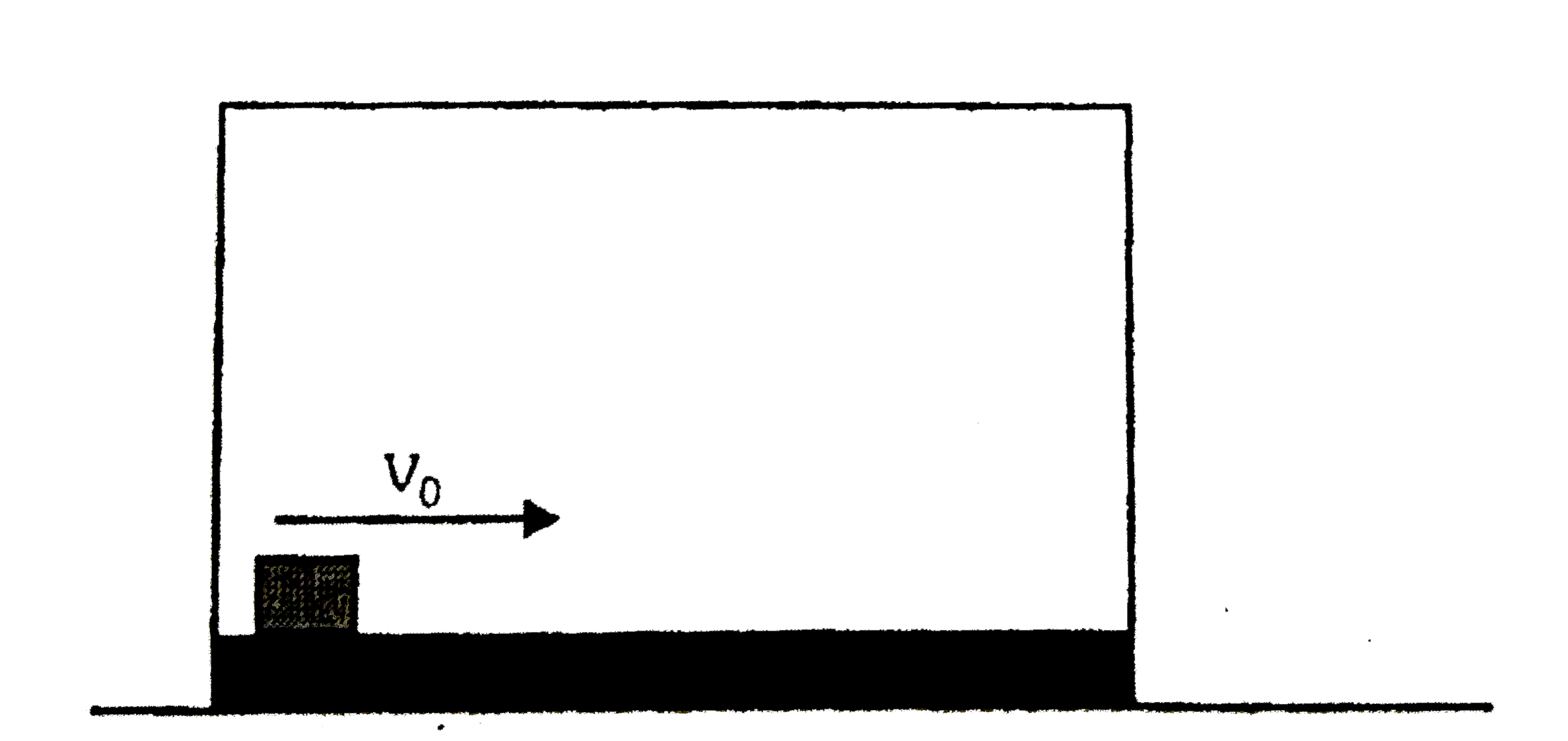 Solution in Gujrati
Solution in Gujrati
0
v0
mMv0
mm+Mv0
The correct Answer is:D
Fext= zero,
→P= constant
Pi=Pf
Finally moving together with velocity v
mv0=(m+M)v
v=mv0(m+M)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionA particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionWith what acceleratin a should the box of figure desecend so that the block of mass M exerts a force Mg/4 on the floor of the box?
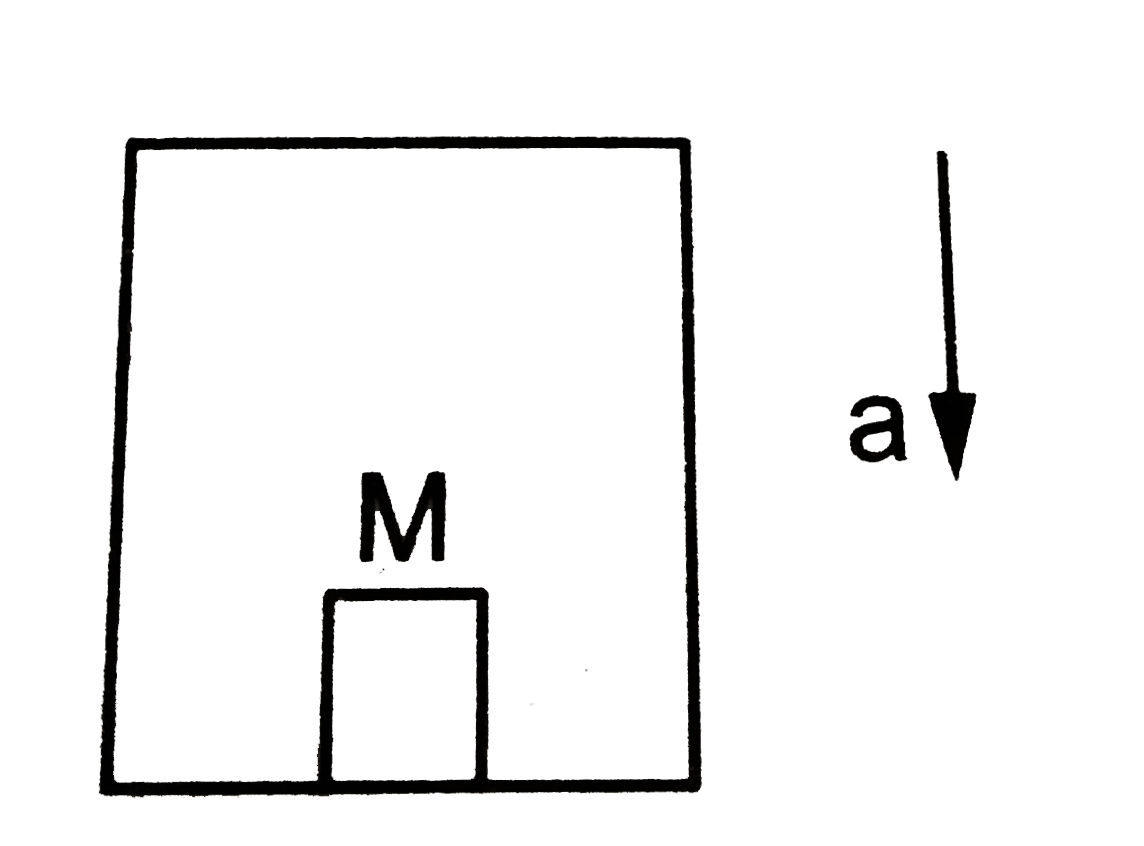
View SolutionWhat should be the acceleration a of the box shown in figure so that the block of mass m exerts a force (mg)/(4) on the force of the box?
View SolutionA bullet of mass 'm' moving with velocity 'u' passes through a wooden block of mass M=nm as shown in figure. The block is resting on a smooth horizontal floor. After passing through the block, velocity relative to the block is
 .
.
View SolutionA block of mass M slides on a frictionless surface with an initial speed of v_(0) On top of block is a small box of mass m. the coefficients of friction between box and block are mu_(6) and mu_(k) . The sliding block encounters and ideal spring with force constant K. Answer following questions. Assuming no relative motion between box and block what is the maximum possible acceleration of block and box at the instant of maximum compression?
View SolutionA block of mass M slides on a frictionless surface with an initial speed of v0 On top of block is a small box of mass m. the coefficients of friction between box and block are μ6andμk. The sliding block encounters and ideal spring with force constant K. Answer following questions. Suppose the value of k is just slightly greater then the value found in previous question, so that the box begins to slide just as the spring reaches maximum compression. The acceleration of box and block are repectively.
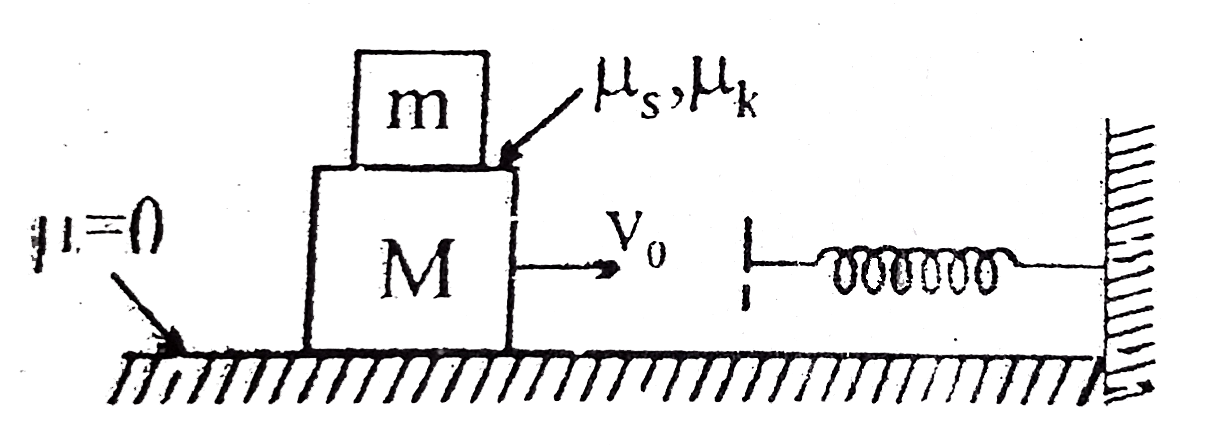
View SolutionA block of mass M slides on a frictionless surface with an initial speed of v0 . On top of block is small box of mass m . The coefficient of friction between box and block are μs and μk . The sliding block encounters an ideal spring with force constant k . Answer the following questions :

Assuming no relative motion between box and block what is the maximum possible acceleration of block and box at the instant of maximum compression ?
View SolutionA block of mass M slides on a frictionless surface with an initial speed of v0 . On top of block is small box of mass m . The coefficient of friction between box and block are μs and μk . The sliding block encounters an ideal spring with force constant k . Answer the following questions :

Suppose the value of k is just slightly greater than the value found in Q.2 , so that the box begins to slide just as the spring reaches maximum compression . The accelerations of box and block are respectively :
View SolutionA block of mass M slides on a frictionless surface with an initial speed of v0 On top of block is a small box of mass m. the coefficients of friction between box and block are μ6andμk. The sliding block encounters and ideal spring with force constant K. Answer following questions. What is maximum value of k for which it remains true that box does not slide?
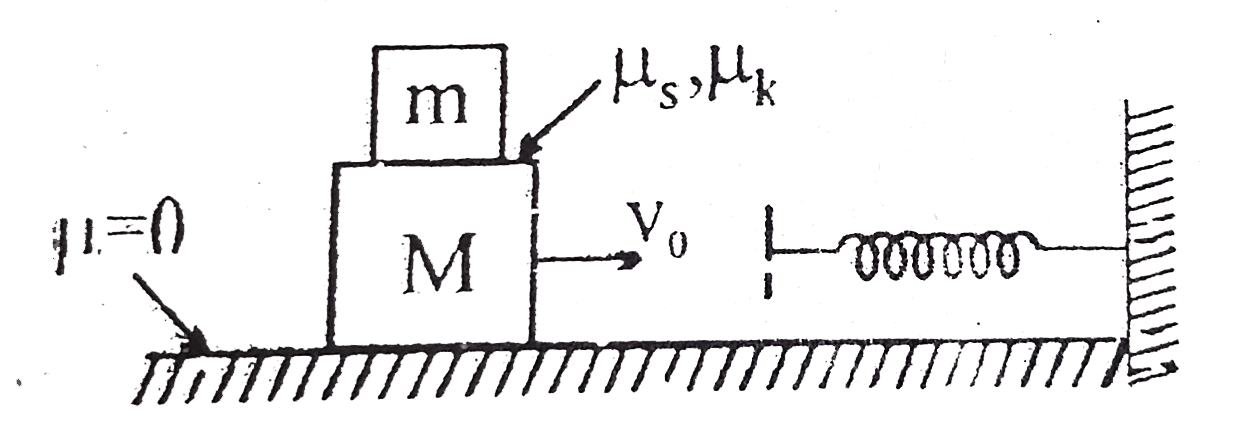
View SolutionA block of mass M slides on a frictionless surface with an initial speed of v0 On top of block is a small box of mass m. the coefficients of friction between box and block are μ6andμk. The sliding block encounters and ideal spring with force constant K. Answer following questions. Suppose the value of k is just slightly greater then the value found in previous question, so that the box begins to slide just as the spring reaches maximum compression. The acceleration of box and block are repectively.
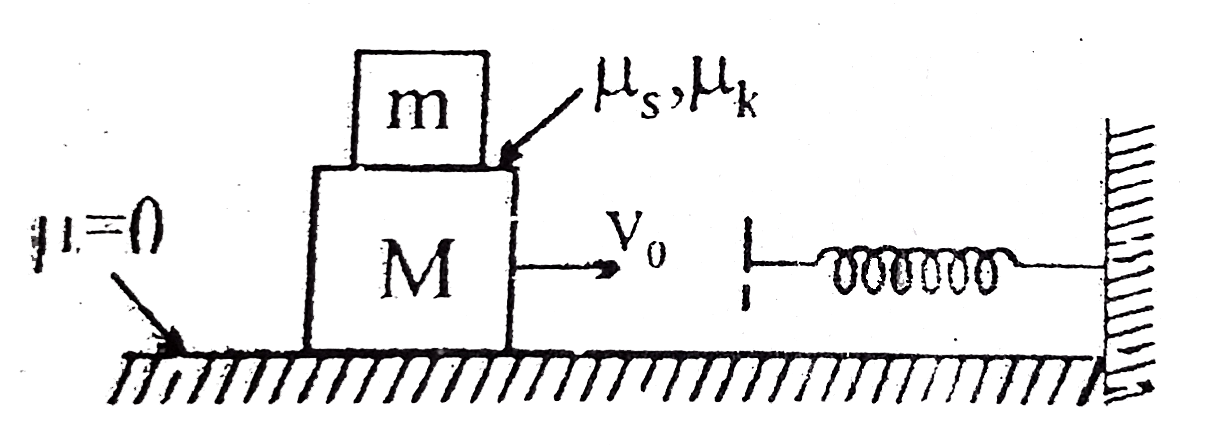
View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View SolutionM द्रव्यमान का एक घनाकार बॉक्स , 4 सेमी आयाम व 2 हर्ट्ज आवृति से क्षैतिज दोलन कर रहा है। इस बॉक्स पर m द्रव्यमान का छोटा - सा ब्लॉक रख दिया जाता है। यदि छोटा ब्लॉक , बड़े ब्लॉक पर से न फिसले तो दोनों ब्लॉकों के बीच घर्षण गुणांक का मान कम से कम होगा।
View Solution
