A bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_ Solution in Gujrati
mv2L−d
mv2L+d
2mv2L−d
2mv2L+d
The correct Answer is:A
Δp= change in momentum =2mv
Δt= time between two collsion 2(L−d)v
∴ Force exerted on wall
=ΔpΔt=mv2(L−d)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
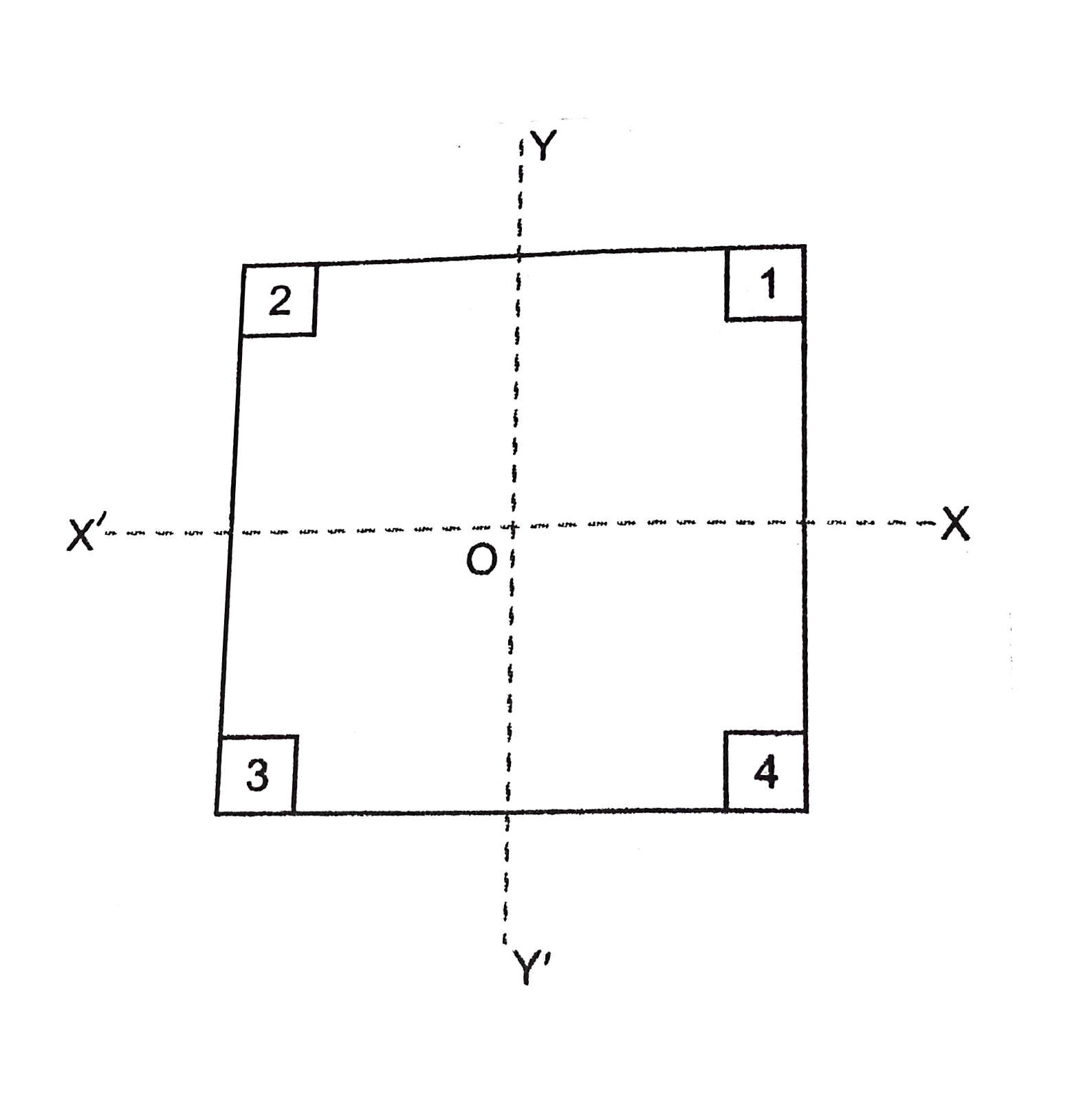
View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionThe centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA sphere of mass m slides with velocity v on as frictionless surface towards a smooth inclined wall as shown in figure. If the collision with the wall is perfectly elastic find a. the impulse imparted by the wall on the sphere b the impulse imparted by the floor on the sphere.
View SolutionA body mass M hits normally a rigid wall with velocity v and bounces back with the same velocity. The impulse experienced by the body is:
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionA ball of mass 0.5 kg moving with a velocity of 2 m//s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA super-ball of mass m is to bounce elastically back and forth between two rigid walls at a distance d from each other. Neglecting gravity and assuming the velocity of super-ball to be v_(0) horizontally, the average force being exerted by the super-ball on each wall is
View SolutionA ball of mass 0.5 kg moving with a velocity of 2ms−1 strikes a wall normally and bounces back with the same speed. If the time of contact between the ball and the wall is one millisecond, the average force exerted by the wall on the ball is
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionA body of mass M hits normally a rigid wall with velocity V and bounces back with the same velocity. The impulse experienced by the body is
View SolutionA body of mass M hits normally a rigid wall with velocity V and bounces back with the same velocity. The impulse experienced by the body is
View SolutionAn intense stream of water of cross-sectional area A strikes a wall at an angle θ with the normal to the wall returns back elastically. If the density of water is ρ and its velocity is v, then the force exerted in the wall will be
View SolutionA super-ball of mass m is to bounce elastically back and forth between two rigid walls at a distance d from each other. Neglecting gravity and assuming the velocity of super-ball to be v_(0) horizontally, the average force being exerted by the super-ball on each wall is
View Solution
