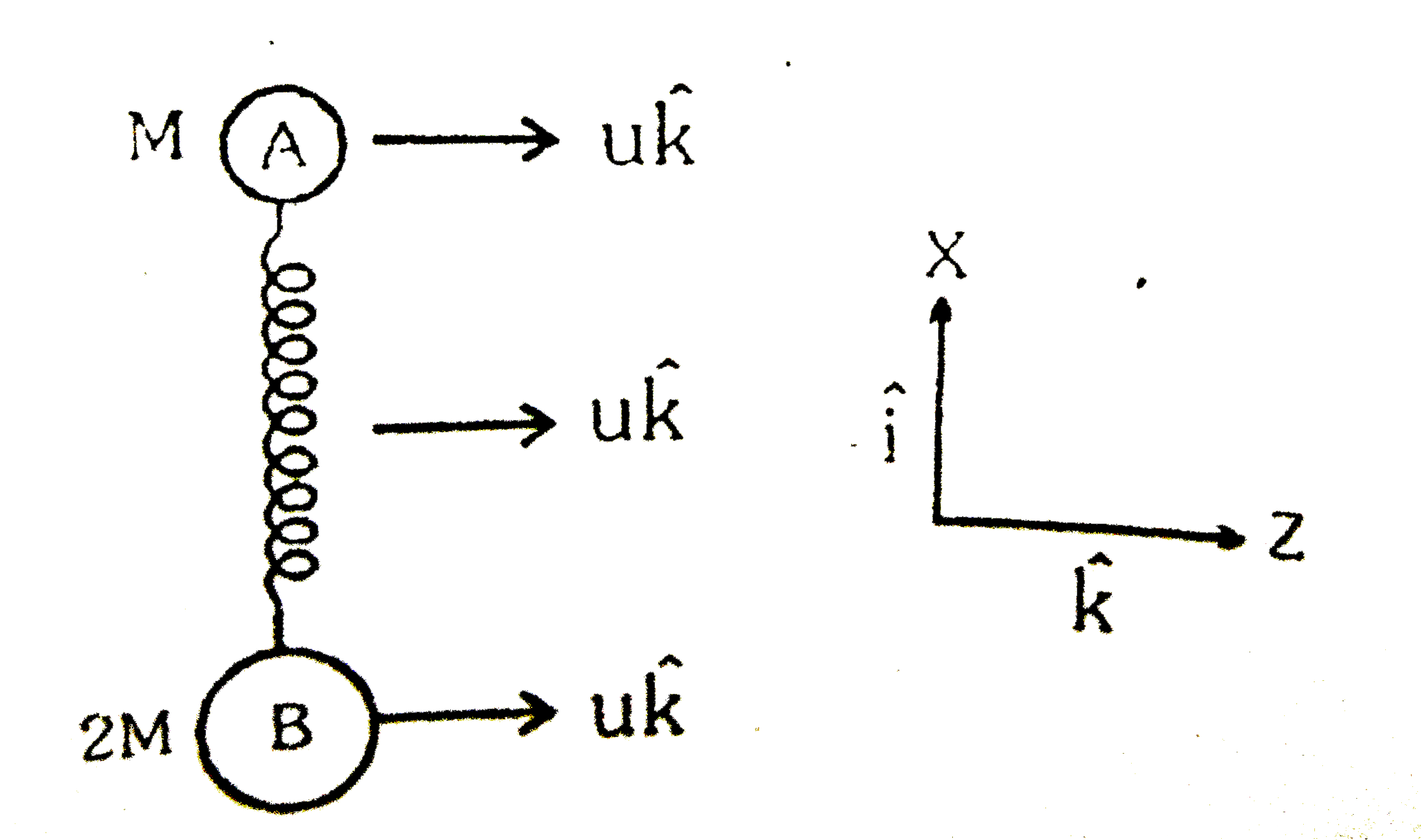
Two masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
 Solution in Gujrati
Solution in Gujrati
vxˆi+uˆk
−vxˆi+uˆk
−2vxˆi+uˆk
2vxˆi+uˆk
The correct Answer is:C
From COLMMVxA+2MvxB=0⇒vxA=−2vxB
so →vA=−2vxˆi+vˆk
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III41videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
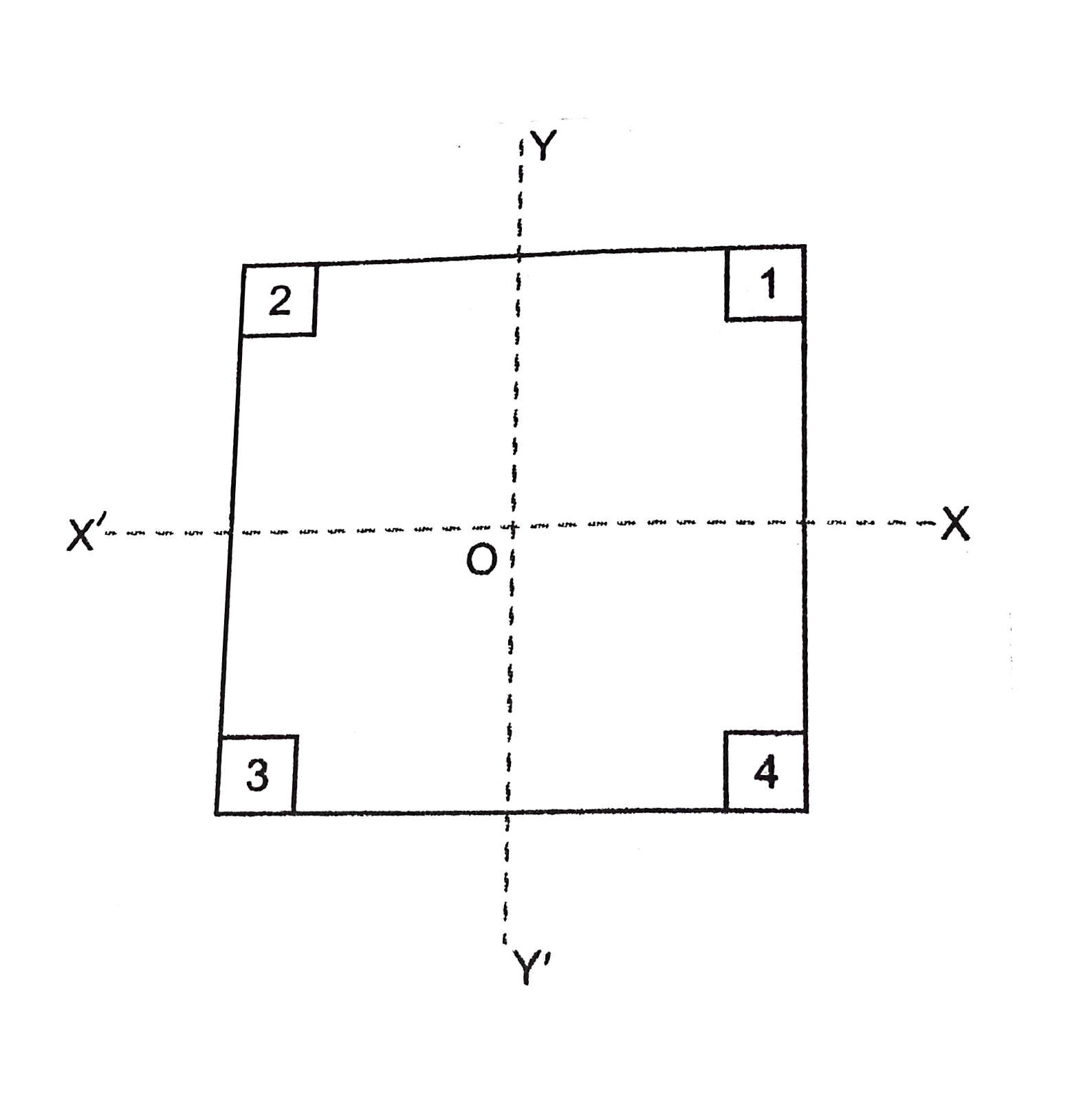
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None04:47View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
 06:16View Solution
06:16View SolutionThe centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
01:53View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.09:19View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
05:58View SolutionTwo bodies A and B of masses m and 2 m respectively are placed on a smooth floor. They are connected by a spring. A third body C of mass m moves with velocity v_0 along the line joining A and B and collides elastically with A as shown in Fig. At a certain instant of time t_0 after collision, it is found that the instantaneous velocities of A and B are the same. Further at this instant the compression of the spring is found to be x_0 . Determine (i) the common velocity of A and B at time t_0 , and (ii) the spring constant.
01:38View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
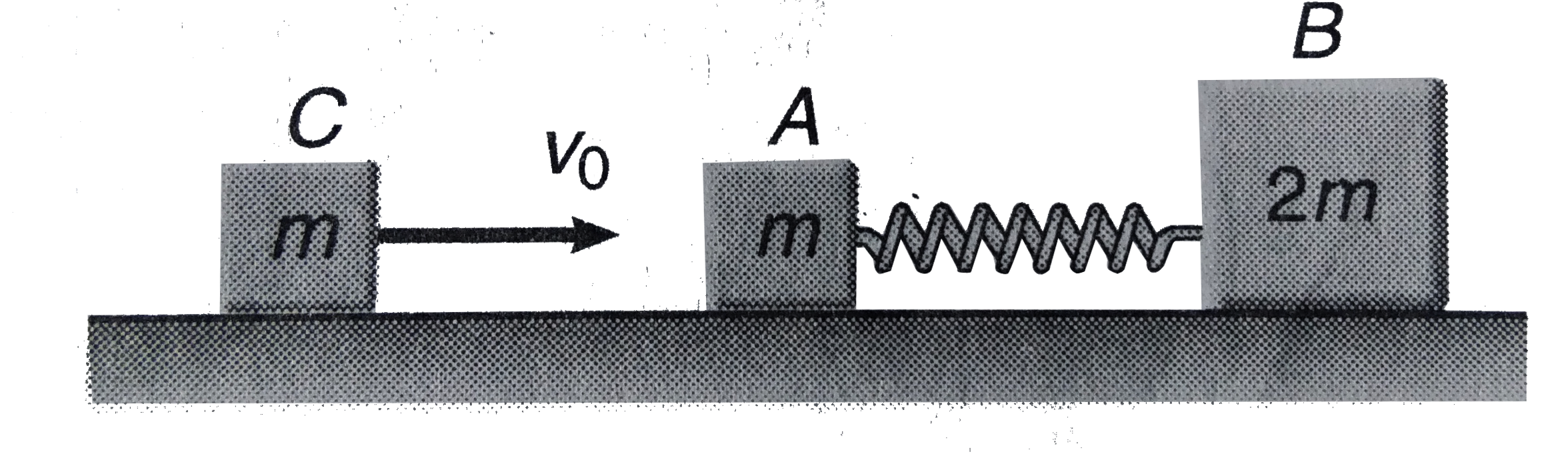 07:22View Solution
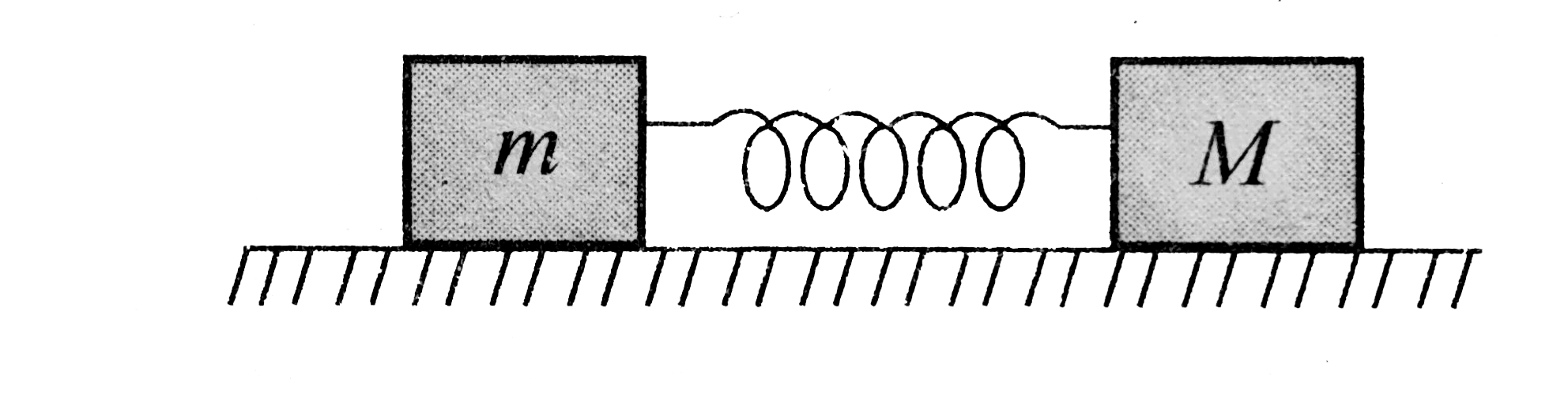
07:22View SolutionAn ideal spring is permanently connected between two blocks of masses M and m. The blocks-spring system can move over a smooth horizontal table along a straight line along the length of the spring as shown in Fig.The blocks are brought nearer to compress the spring and then released. In the subsequent motion,
 02:21View Solution
02:21View SolutionConsider the system shown below, with two equal masses m and a spring with spring constant K. The coefficient of friction between the left mass and horizontal table is μ=1/4, and the pulley is frictionless. The spring connecting both the blocks is massless and inelastic. The system is held with the spring at its unstretched length and then released.
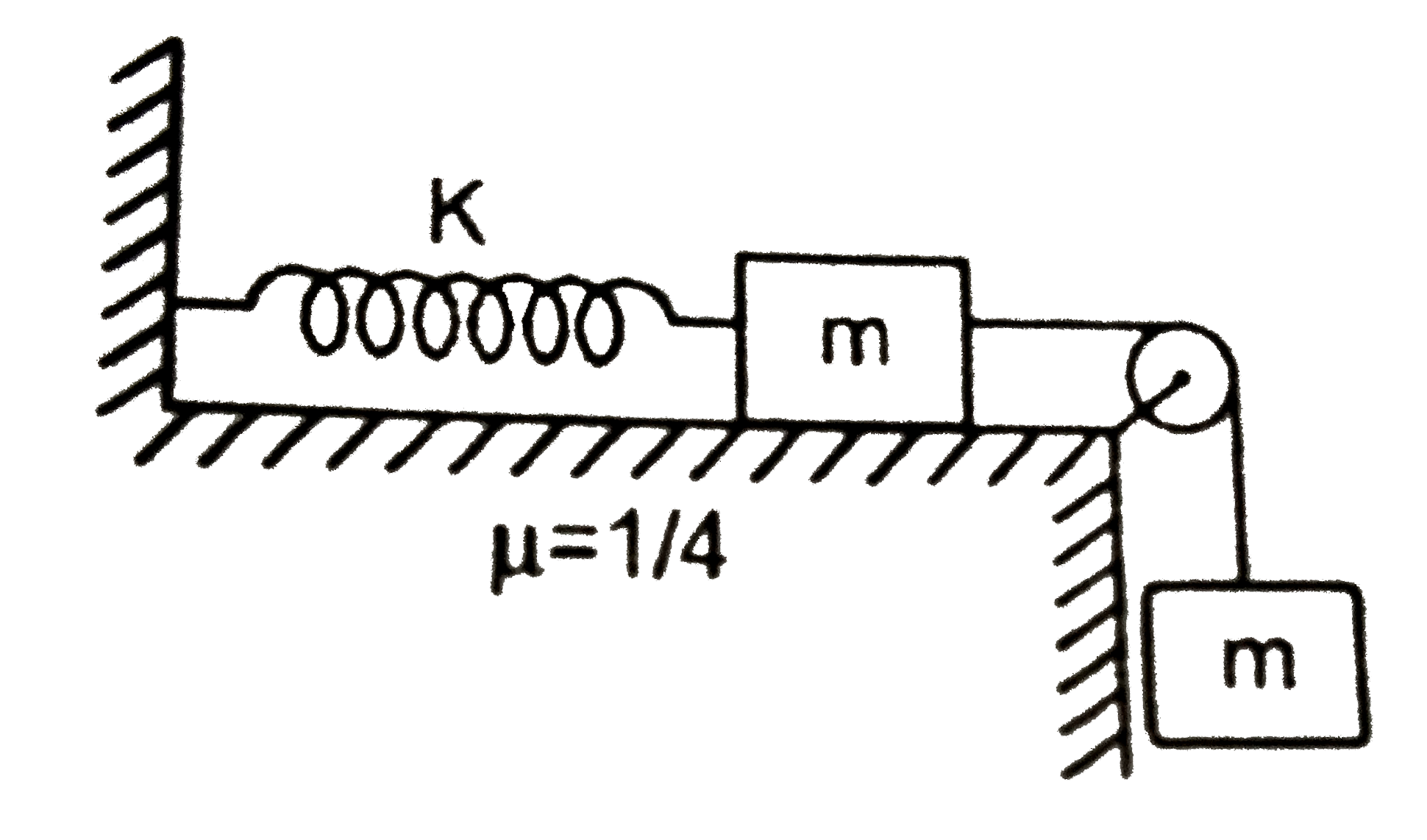
If the string connecting both the masses is cut just at the instant both masses came to momentary rest for the first time in question 5, then maximum compression of spring during resulting motion is (Take μ=1/4)06:45View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere Acceleration of centre of mass of system comprising A and B just after A is released is
06:08View SolutionTwo ring of mass m and 2m are connected with a light spring and can slide over two frictionless parallel horizontal rails as shown in figure. Ring of mass m is given velocity 'v0' in horizontal direction as shown. Calculate the maximum stretch in spring during subsequent motion.
 View Solution
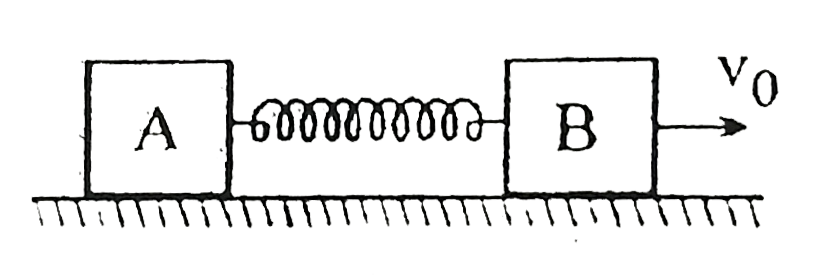
View SolutionTwo blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
 06:19View Solution
06:19View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
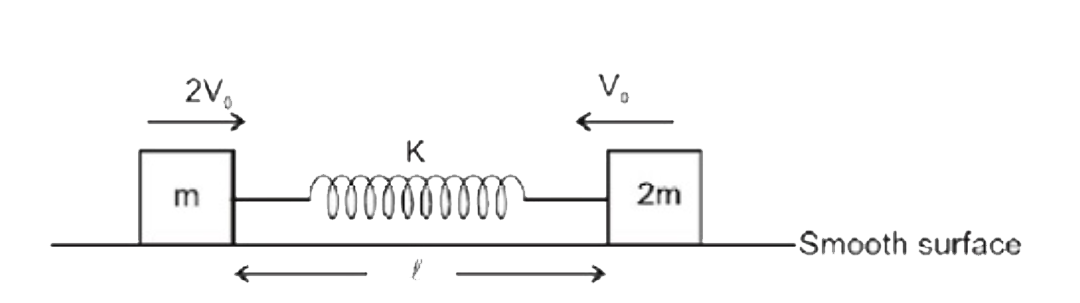
03:05View SolutionTwo blocks A and B of masses m and 2m respectively, attached at opposite ends of a spring of constant K, placed on a smooth horizontal surface. Spring is initially at its natural length l. A is given a velocity 2V0 and B given velocity V0 as shown.
Maximum separation between m and centre of mass of the system will be :03:28View SolutionTwo rectangular blocks A and B of masses 2 kg and 3 gk respectively are connected by a spring of spring constant 10.8Nm^(-1) and are placed on a frictionless horizontal surface. The block A was given an initial velocity of 0.15 ms^(-1) in the direction shown in the figure. The maximum compression of the spring during the motion is
02:02View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity V, along the line joining A and B and collides elastically with A, as shown in figure. At a certain instant of time t, after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0 and (ii) the spring constant.
 04:16View Solution
04:16View Solution

