A ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
500N
1000N
2000N
3000N
The correct Answer is:3
To solve the problem, we need to calculate the average force exerted by the wall on the ball when the ball strikes the wall and bounces back. We can follow these steps:
Step 1: Identify the given values
- Mass of the ball, m=0.5kg
- Initial velocity of the ball, vi=2m/s (towards the wall)
- Final velocity of the ball, vf=−2m/s (away from the wall, hence negative)
- Time of contact with the wall, t=1ms=1×10−3s
Step 2: Calculate the change in momentum
The change in momentum (Δp) can be calculated using the formula:
Δp=pf−pi
Where:
- pf=m⋅vf
- pi=m⋅vi
Calculating pi and pf:
pi=m⋅vi=0.5kg⋅2m/s=1kg m/s
pf=m⋅vf=0.5kg⋅(−2)m/s=−1kg m/s
Now, substituting these values to find Δp:
Δp=−1kg m/s−1kg m/s=−2kg m/s
Step 3: Calculate the average force
The average force (F) can be calculated using the formula:
F=Δpt
Substituting the values we found:
F=−2kg m/s1×10−3s=−2000N
The negative sign indicates that the force exerted by the wall is in the opposite direction of the ball's initial motion. Therefore, the magnitude of the average force exerted by the wall on the ball is:
F=2000N
Final Answer
The average force exerted by the wall on the ball is 2000 N.
---
- Mass of the ball, m=0.5kg
- Initial velocity of the ball, vi=2m/s (towards the wall)
- Final velocity of the ball, vf=−2m/s (away from the wall, hence negative)
- Time of contact with the wall, t=1ms=1×10−3s
The change in momentum (Δp) can be calculated using the formula:
Δp=pf−pi
Where:
- pf=m⋅vf
- pi=m⋅vi
pi=m⋅vi=0.5kg⋅2m/s=1kg m/s
pf=m⋅vf=0.5kg⋅(−2)m/s=−1kg m/s
Δp=−1kg m/s−1kg m/s=−2kg m/s
The average force (F) can be calculated using the formula:
F=Δpt
Substituting the values we found:
F=−2kg m/s1×10−3s=−2000N
F=2000N
The average force exerted by the wall on the ball is 2000 N.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A ball of mass 2 kg is moving with velocity 20 m/sec strikes with the surface and rebounds with same speed, if time of contact is 0.1 sec then calculate average force on the ball.
View SolutionA cricket ball of mass 150 kg is moving with a velocity of 12m/s and is hit by a bat so that ball is turned back with a velocity of 20m/s . The force of the blow acts for 0.01 s on the ball . Find the average force exerted by the bat on the ball.
View Solution
Knowledge Check
A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘tA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2mu
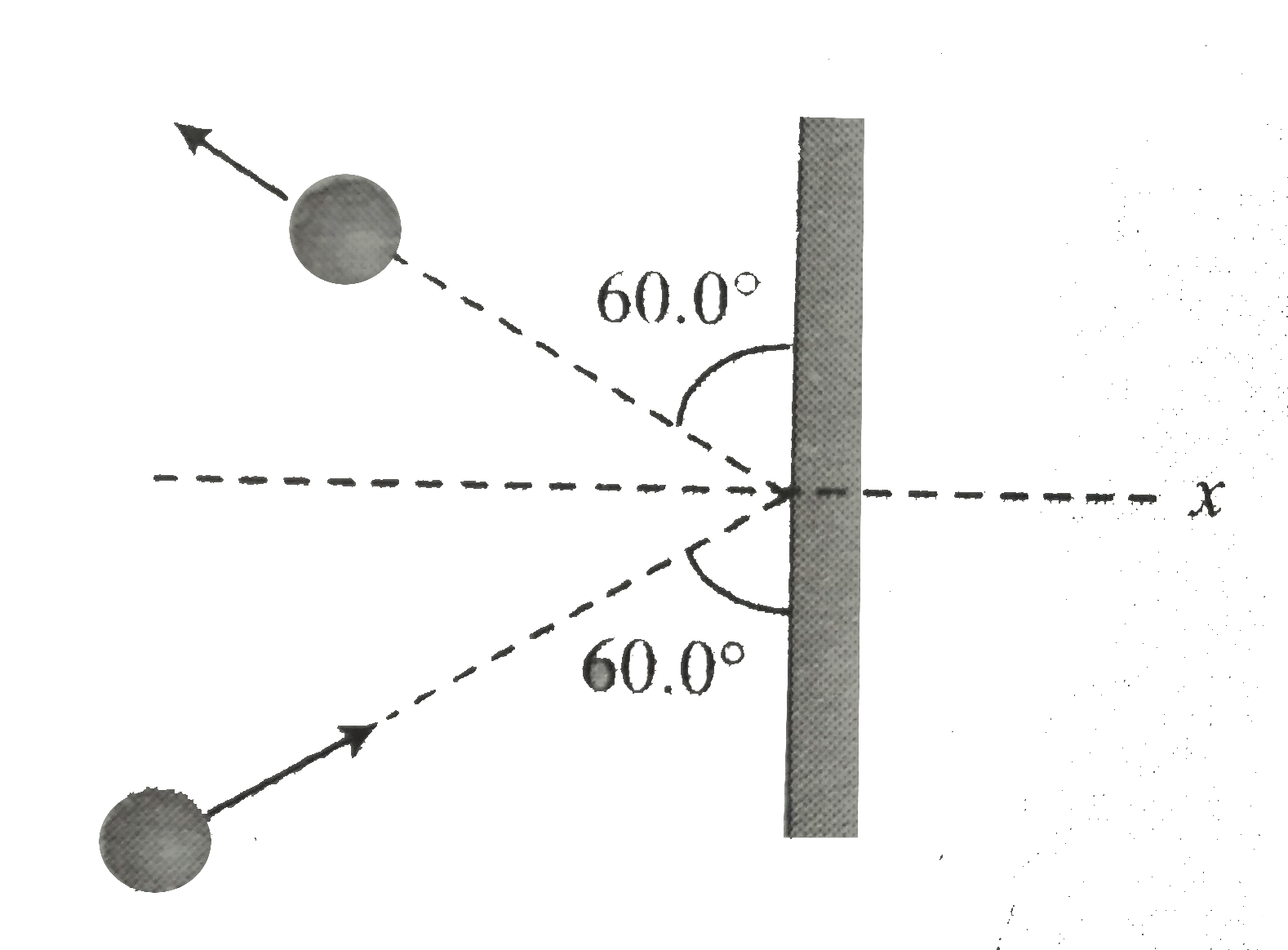
A 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle 60∘ (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA rubber ball of mass 0.4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0.4 s, find the average force exerted by the ball on the ground .
View SolutionA ball of mass 'm' is thrown with a speed v0 towards a bat. It rebounds along the same speed 2v0 . The variation of interaction force between the bat and ball is shown
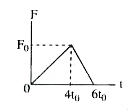
Average force exerted by the bat on the ball is
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View Solution
