A particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)NoneSolution in Gujrati
The correct Answer is:(A) → q; (B) → r; (C ) → p
For 1kgv1=(2t)ˆj=4ˆi,a1=2ˆi=2ˆi
for 2kgv2=t2ˆj=4ˆj,a2=2tˆj=4ˆj
(A) Acceleration of centre of mass =m1a1+m2a2m1+m2
→acm=23ˆi+83ˆj⇒acm=√49+649⇒√683m/s2
f=macm=√68N
(B) Velocity of centre of mass
→vcm=m1v1+m2v2m1+m2=(43ˆi+83ˆj)m/s
⇒|→vcm|=√169+649⇒√803
(C ) →vcm=1(2t)ˆi+2(t2ˆj)1+2+23tˆi+23t2ˆj
Displacement =∫20→vcmdt=[32(t22)2ˆi+23(t33)ˆj]20=43ˆi+169ˆj
⇒|Dispalcement|=√(43)2+(169)2=209 unit
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
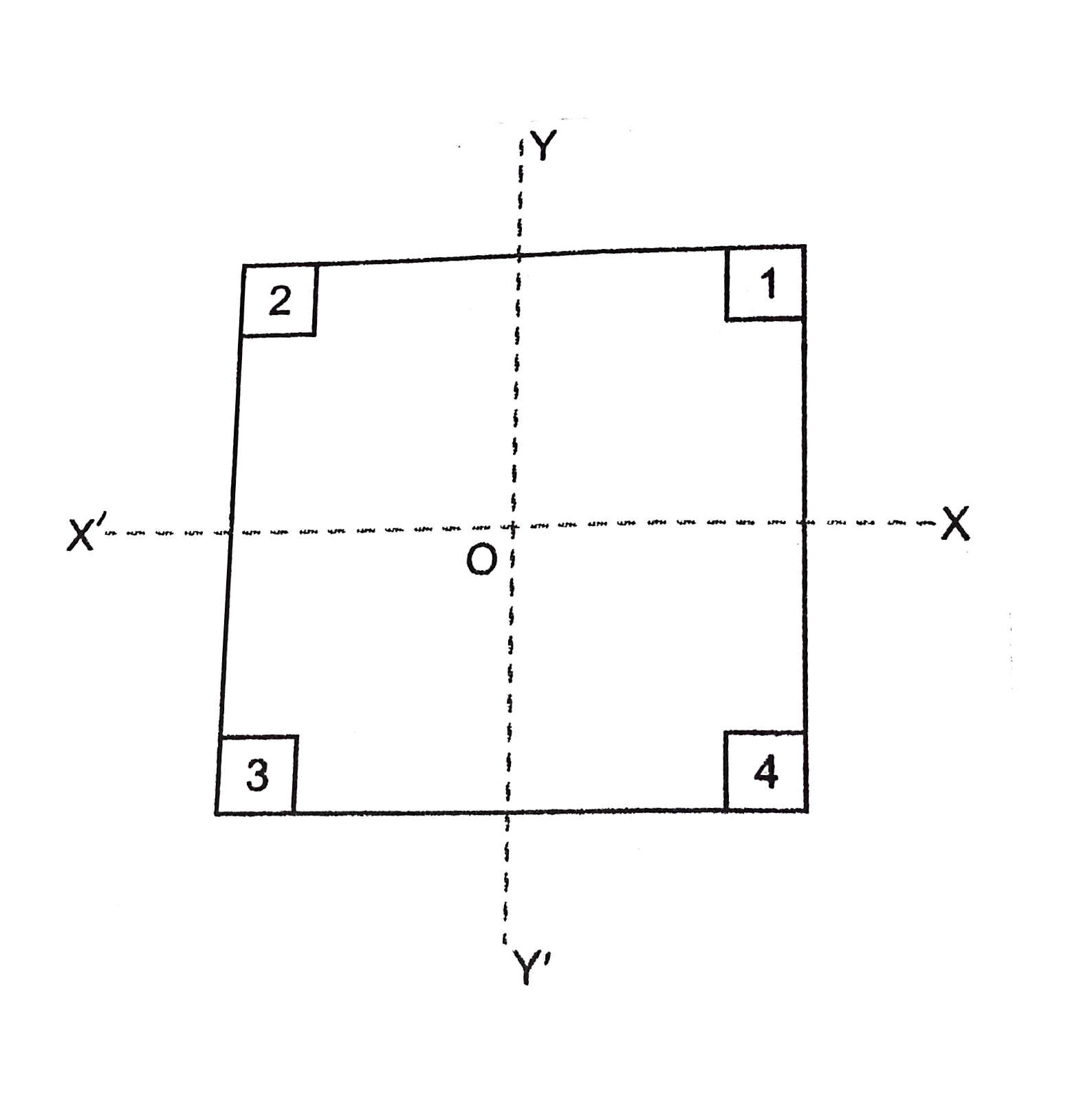
Fig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionTwo particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionTwo particles of equal mass have velocities →v1=2ˆi=m/s−1 and →v2=2ˆjm/s−1. First particle has an acceleration →a1=(3ˆi+3ˆj)ms−2 while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of.
View SolutionA particle of mass 1kg has velocity →v1=(2t)ˆi and another particle of mass 2kg has velocity →v2=(t2)ˆj
Column IColumn II(A)Netforce on centre of mass at 2 s(p)209unit(B)Velocity of centre of mass at 2 s(q)√68 unit(C)Displacement of centre of mass in 2s(r)√803unit(s)None
View SolutionA force vec(F)=(2hat(i)+hat(j)+3hat(k)) N acts on a particle of mass 1 kg for t = 2s. If initial velocity of particle is vec(u)=(2hat(i)+hat(j))ms^(-1) , then the speed of particle at the t = 2 s will be
View SolutionTwo bodies of masses 10 kg and 2 kg are moving with velocities 2ˆi−7ˆj+3ˆk and −10ˆi+35ˆj−3ˆjms−1 respectively. Find the velocity of the centre of mass of the system.
View SolutionA charged particle of specific charge (i.e charge per unit mass) 0.2 C/kg has velocity 2 hat(i) - 3 hat(j) (m/s) at some instant in a uniform magnetic field 5 hat(i) + 2 hat(j) (tesla). Find the acceleration of the particle at this instant
View SolutionA particle of mass 2 kg moving with a velocity v1=(2ˆi−3ˆj)m/s experience a perfectly inelastic collision with another particle of mass 2 kg having velocity →v2=(3ˆj+6ˆk)m/s. Find the velocity and speed of the particle formed.
View SolutionA particle of mass 2sqrt(5) Kg is having velocity vec v=(2hat i+hat j)m/s " and acceleration vec a=(hat j-hat i)m/s^(2) " at some instant of time. At same instant find component of net force (in N) parallel to velocity.
View SolutionThe velocity of a particle of mass 2 kg is given by vec(v)=at hat(i)+bt^(2)hat(j) . Find the force acting on the particle.
View SolutionIf the velocity is →v=2ˆi+t2ˆj−9→k, then the magnitude of acceleration at t = 0 . 5 s is :
View SolutionA particle of mass 1 kg has velocity vecv_(1)=(2t)hati and another particle of mass 2 kg has velocity vecv_(2)=(t^(2))hatj . Net force on the centre of mass at 2 s
View SolutionA particle of mass 1 kg has velocity vecv_(1)=(2t)hati and another particle of mass 2 kg has velocity vecv_(2)=(t^(2))hatj . Velocity of the centre of mass at 2 s
View Solution
