Statement I: If a sphere of mass mmoving with speed u undergoes a perfectly elastic head-on collision with another sphere of heavier mass M at rest (M>m), then direction of velocity of sphere of mass m is reversed due to collision (no external force acts on system of two spheres).
Statement II: During a collision of spheres of unequal masses, the heavier mass exerts more force on the lighter mass in comparison to the force which lighter mass exerts on the heavier one,Solution in Gujrati
Statement -1 is True, Statement -2 si True , Statement -2 is a correct explanation for Statement -1.
Statement -1 is True, Statement -2 si True , Statement -2 is not correct explanation for Statement -1.
Satement-1 is True, Statement-2 is Satement-1 is True, Statement-2 is False.False.
Satement-1 is False, Statement-2 is True.
The correct Answer is:C
Step by step video & image solution for Statement I: If a sphere of mass mmoving with speed u undergoes a perfectly elastic head-on collision with another sphere of heavier mass M at rest (M gt m), then direction of velocity of sphere of mass m is reversed due to collision (no external force acts on system of two spheres). Statement II: During a collision of spheres of unequal masses, the heavier mass exerts more force on the lighter mass in comparison to the force which lighter mass exerts on the heavier one, by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
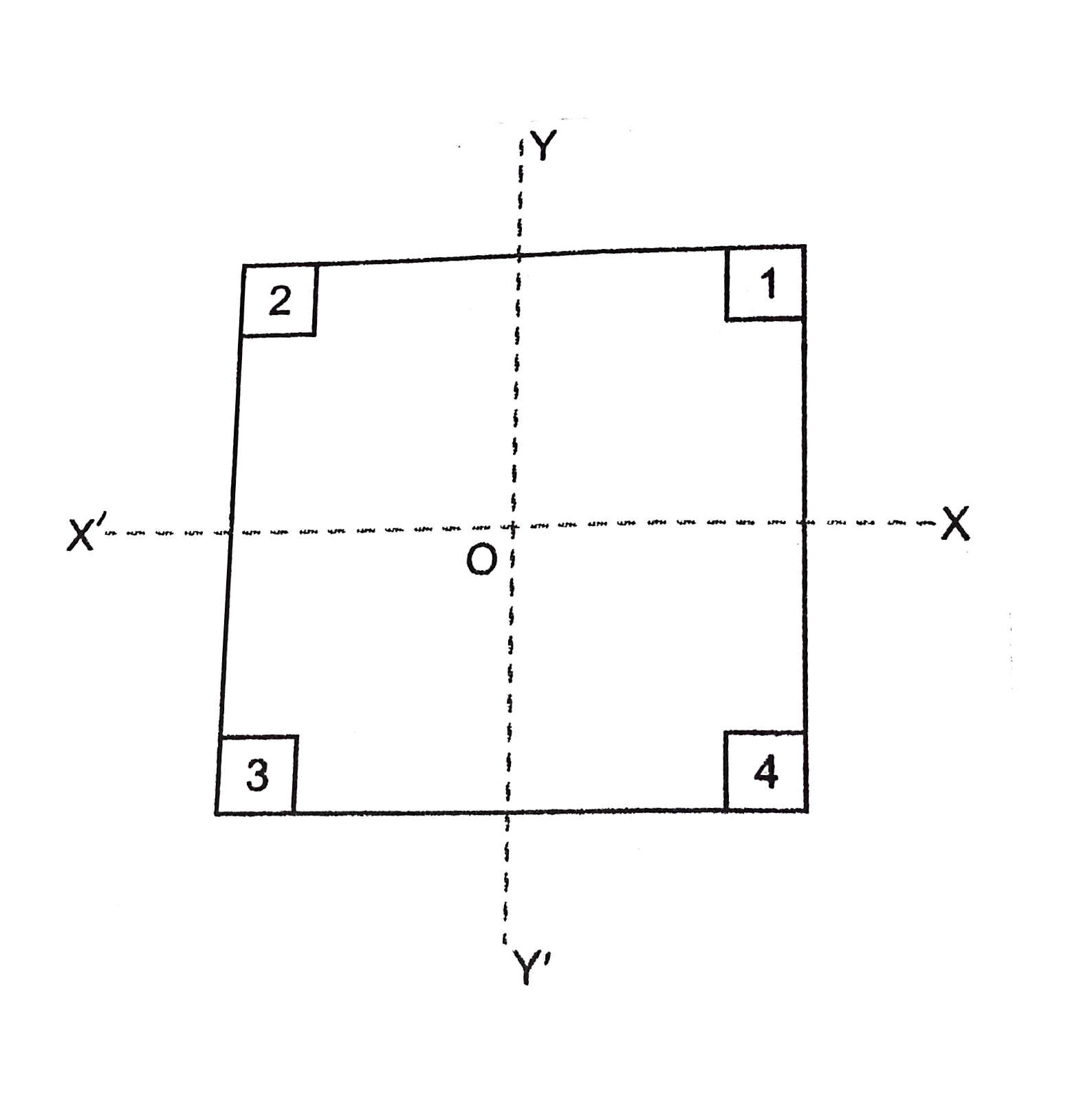
Fig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionTwo particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionStatement I: If a sphere of mass m moving with speed u undergoes a perfectly elastic head-on collision with another sphere of heavier mass M at rest ( M gt m ), then direction of velocity of sphere of mass m is reversed due to collision (no external force acts on system of two spheres). Statement II: During a collision of spheres of unequal masses, the heavier mass exerts more force on the lighter mass in comparison to the force which lighter mass exerts on the heavier one,
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA sphere P of mass m and velocity v_i undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle theta between the velocities of the spheres after the collision shall be
View SolutionA sphere of mass 'm' moving with velocity 'v' collides head-on on another sphere of same mass which is at rest. The ratio of final velocity of second sphere to the initial velocity of the first sphere is (e is coefficient of restitution and collision is inelastic)
View SolutionA body of mass M moving with a speed u has a ‘head on’, perfectly elastic collision with a body of mass m initially at rest. If M > > m , the speed of the body of mass m after collision, will be nearly :
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA sphere of mass M moving with velocity w collides elastically with another of mass m at rest. After collision their final velocities are V and v. The value of vis:
View SolutionA sphere of mass M moving with velocity u collides elastically with another of mass mat rest. After collision their final velocities are V and v. The value of v is:
View SolutionA sphere of mass m moving with a velocity u hits another sphere of same mass at rest. If e is the coefficient of restitution then the ratio of velocities of two spheres after collision will be :
View SolutionA sphere of mass M,, moving with a velocity V0 collides head on with a stationary sphere of mass M. The collision is elastic. V1 and V2 are respectively their velocities immediately after collision.
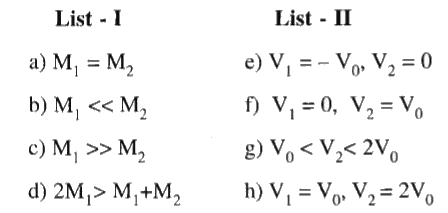
View SolutionA sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
View Solution
