A 70g ball B dropped from a height h0=9m reaches a height h2=0.25m after bouncing twice from identical 210g plates. Plate A rests directly on hard ground, while plate C rests on a foam-rubber mat. Determine
(i) the coefficient of restituation between the ball and the plates,
(ii) the height h1 of the ball's first bounce. Solution in Gujrati
The correct Answer is:(i) 0.66 (ii) 4m
For first collision with plate A, final velocity of ball v1=ev0=e√2gh0 ….(i)
For second collision mv=4mv'⇒v'=v4
⇒e√2gh04=√2gh2⇒e=23
Height attained after first collision
∴h1=e2h0=23×23×9=4m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
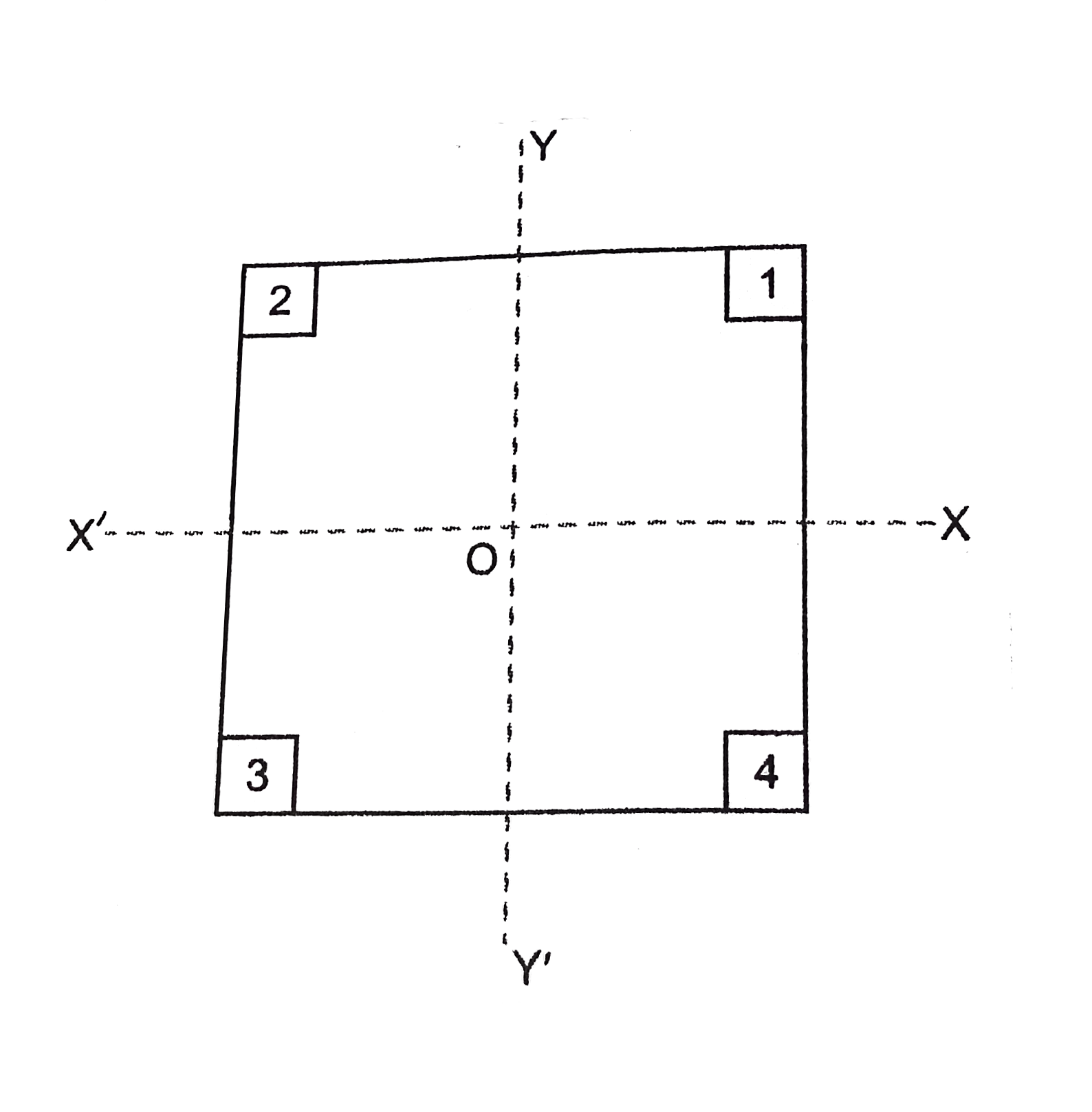
View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA steel ball is dropped on a hard surface from a height of 1m and rebounds to a height of 64cm . The maximum height attained by the ball after n^(th) bounce is (in m)
View SolutionA metal ball falls from a height of 32 metre on a steel plate. If the coefficient of restitution is 0.5, to what height will the ball rise after second bounce
View SolutionA ball is dropped from rest from a height of 0m. If it loses 20% of its kinetic energy on striing the ground, what is the height to which the ball bounces?
View SolutionA metal ball falls from a height of 1m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball and steel plate is
View SolutionA ball at rest is dropped from a height of 12 m. It losses 25% of its kinetic energy on striking the ground and bounces back to a height 'h'. then value of 'h' is
View SolutionA ball is dropped from rest from a height of 10 m. if it loses 20% of its KE on striking the ground ,what is the height to which the ball bounces ?
View SolutionA small steel ball bounces on a steel plate held horizontally. On each bounce the speed of the ball arriving at the plate is reduced by a factor e (coefficient of restitution) in the rebound , so that V_("upward")=eV_("downward") If the ball is initially dropped from a height of 0.4m above the plate and if 10s later the bouncing ceases, the value of e is
View SolutionA ball at rest is dropped freely from a height of 20 m. It loses 30% of its energy on striking the ground and bounces back. The height to which it bounces back is
View SolutionA ball at rest is dropped freely from a height of 20m. It loses 30% of its energy on striking the ground and bounces back. The height to which it bounces back is
View SolutionA ball at rest is dropped freely from a height of 20m. It loses 30% of its energy on striking the ground and bounces back. The height to which it bounces back is
View Solutionएक गेंद को 10 m ऊँचाई से गिराया जाता है। यदि भूमि तल से टकराने के बाद गेंद की ऊर्जा 40% कम हो जाती है, तो गेंद वापस कितनी ऊँचाई तक उछलेगी?
View Solution
