After a completely inelastic collision two objects of the same mass and same initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.Solution in Gujrati
The correct Answer is:120∘
2mucos.θ2=2mv
⇒v=ucos.θ2=u2
⇒cosθ2=12,θ2=60∘,θ=120∘

Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
Two identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
02:55View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
02:07View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
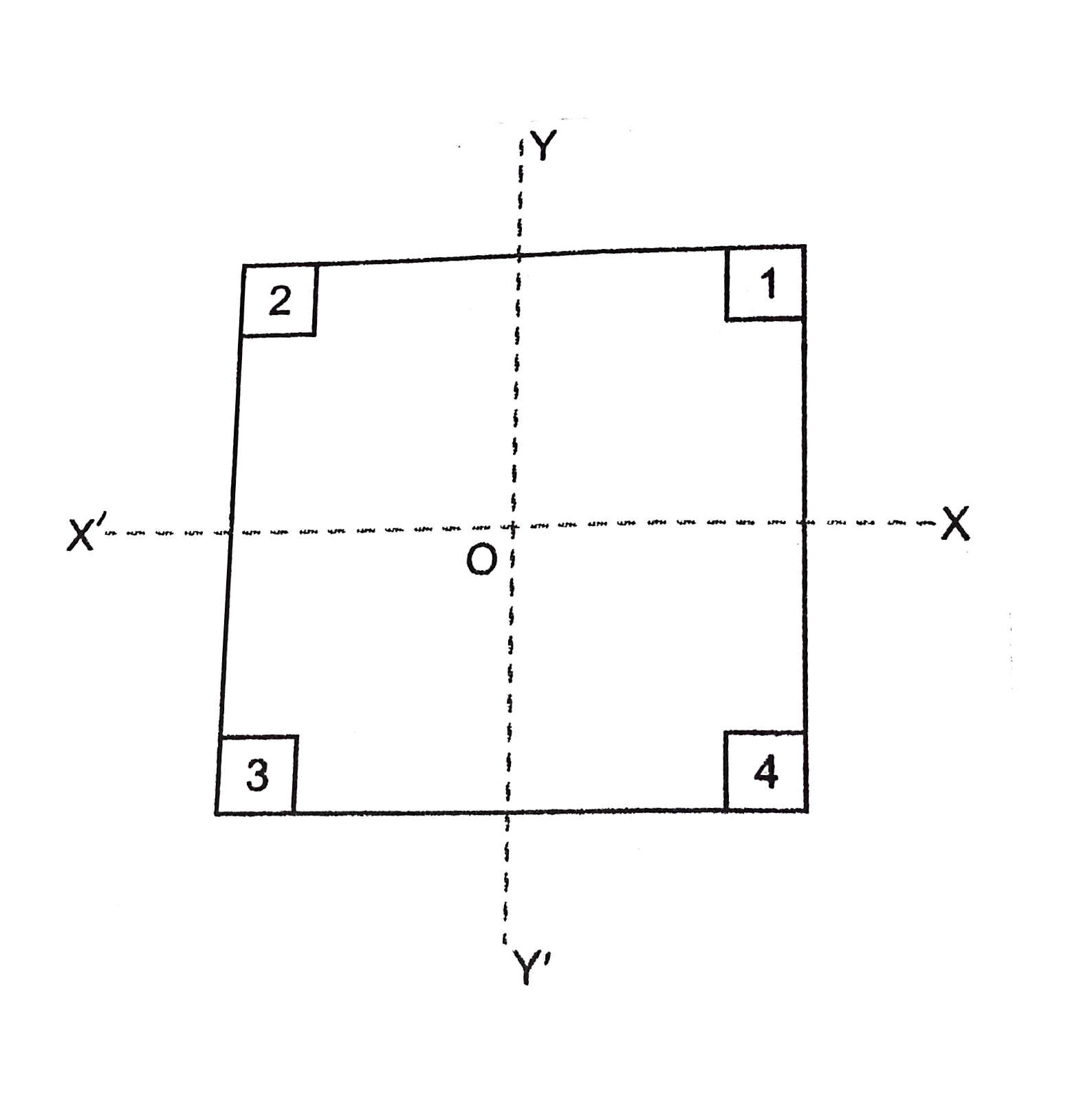 04:30View Solution
04:30View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.04:00View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionAfter a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
View SolutionAfter a completely inelastic collision two objects of the same mass and same initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the particles become half the initial speed. Find the angle between the two before collision.
View SolutionAfter a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the particles become half the initial speed. The angle between the velocities of the two before collision is:
02:51View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the spee of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
02:38View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the particles became half the initial speed. The angle between the velocities of the two before collision is
02:15View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the particles became half the initial speed. The angle between the velocities of the two before collision is
04:10View SolutionAfter perfectly inelastic collision between two identical particles moving with same speed in different directions, the speed of the combined particle becomes half the initial speed of either particle. The angle between the velocities of the two before collision is
View Solution

