A cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
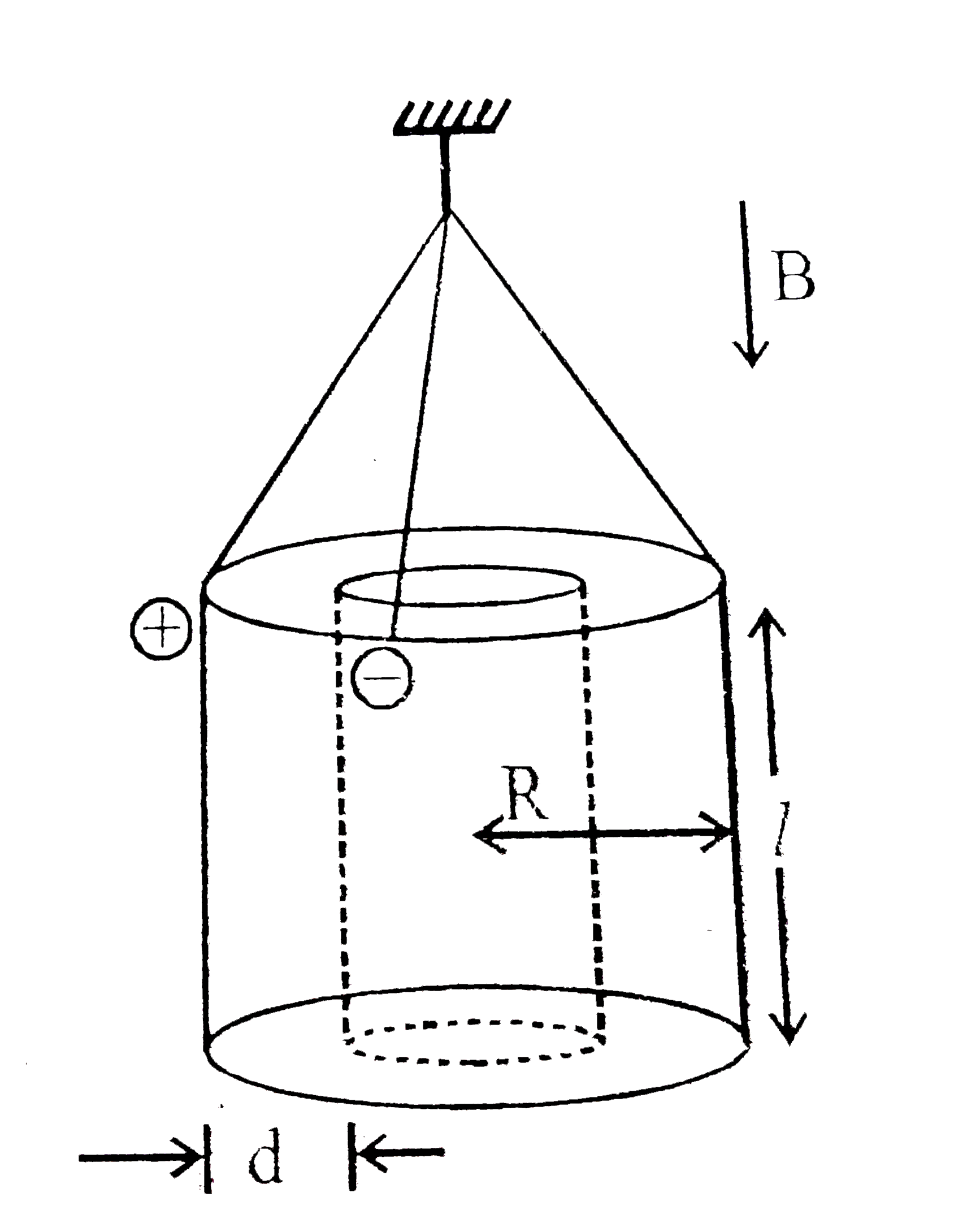
If without being mechaically disturbed, the capacitor is discharged through an internal radial wire then find maximum angular velocity of capacitor
π∈0VBlM
2π∈0VBlM
3π∈0VBLM
4π∈0VBLM
The correct Answer is:B
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
18 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
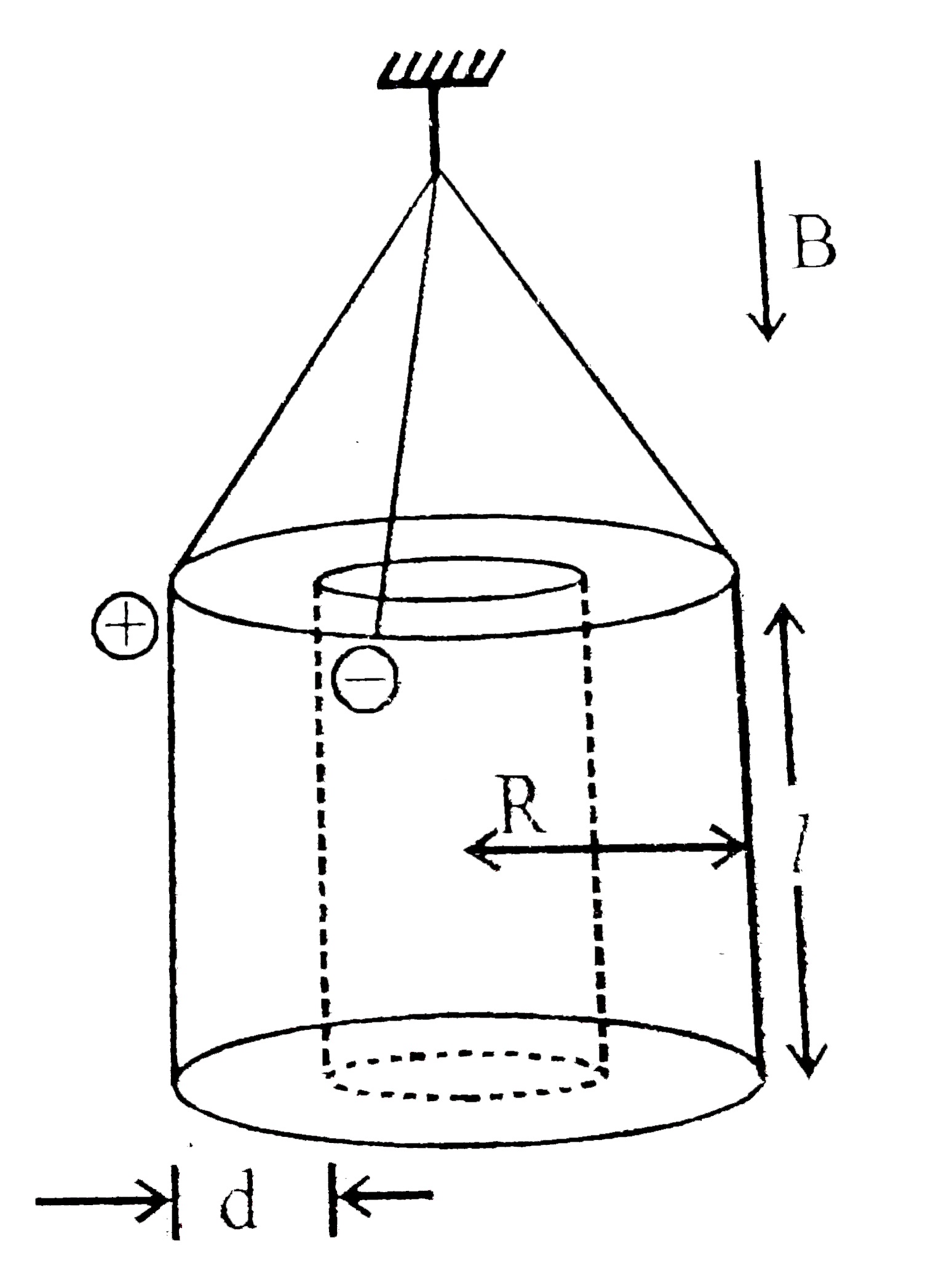
Choose CORRECT statement
View SolutionA cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
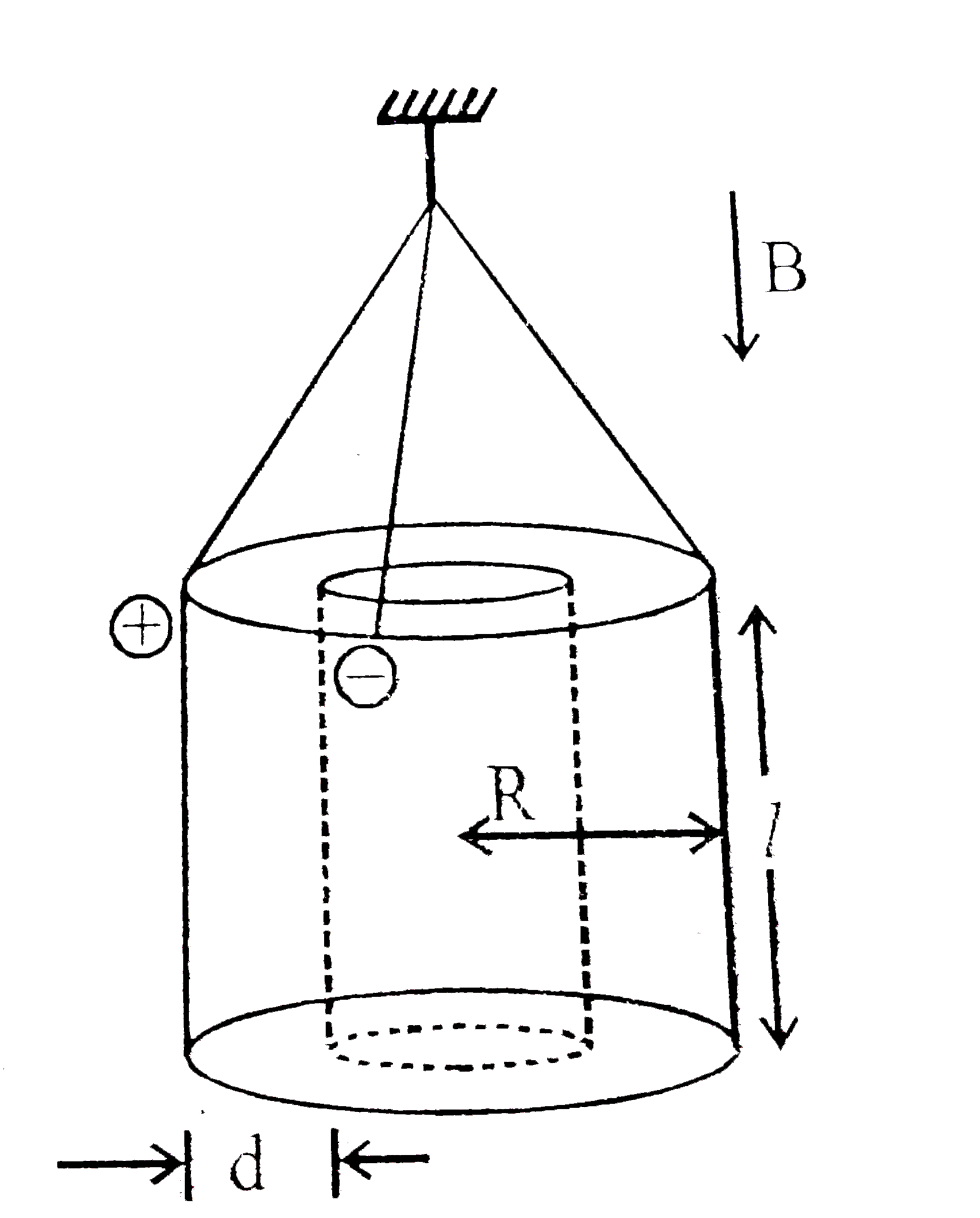
Charge on capacitor is given by
View Solution
Knowledge Check
A cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
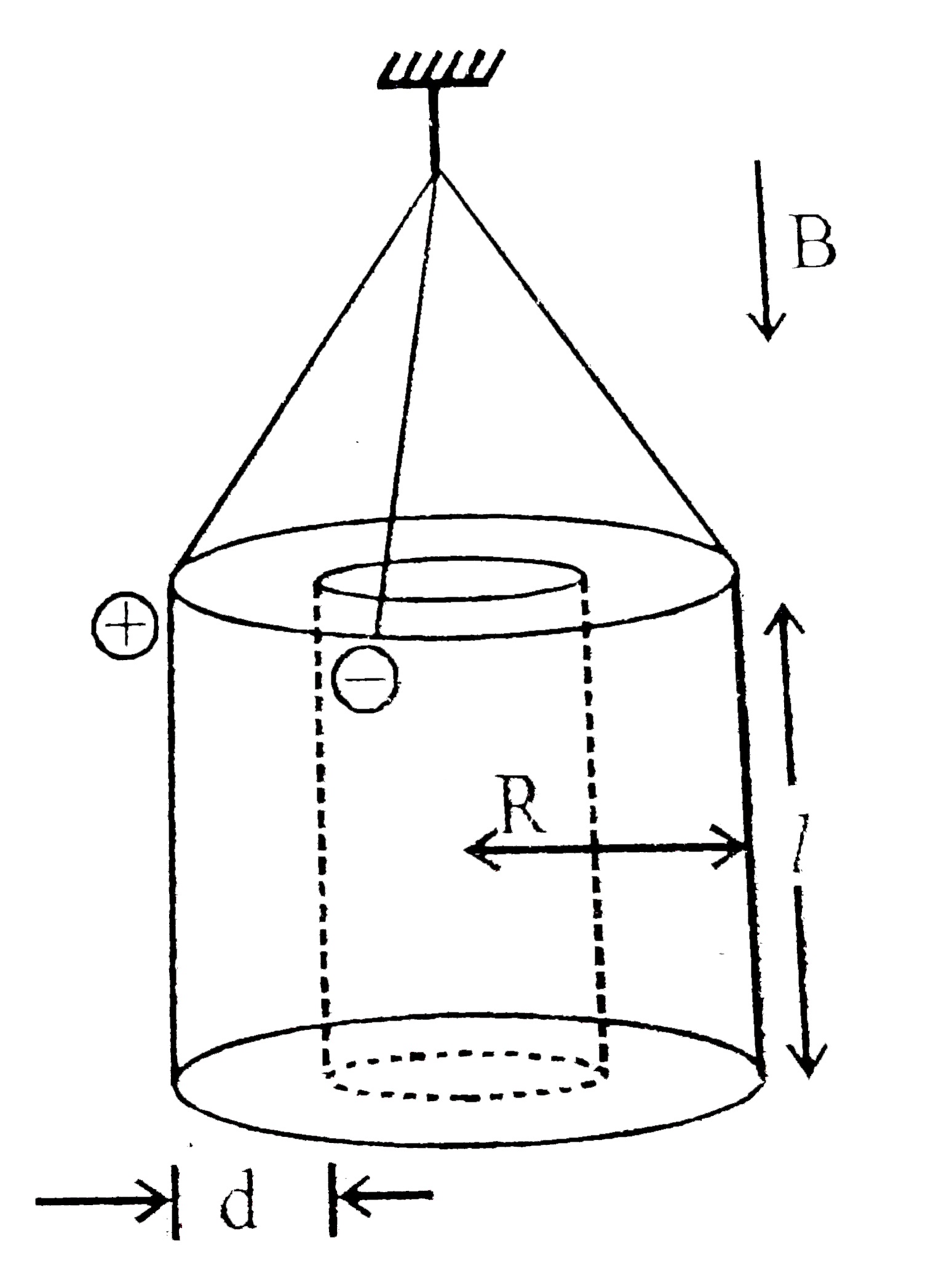
Choose CORRECT statementAWhen capacitor is discharged through radial wire then value of ωmax depends on values of R and dBValue of ωmax is independent of time dependence of discharge currentCValue of ωmax is dependent on time dependence of discharge currentDValue of ωmax cannot be calculated with the help of given data.A cylindrical capacitor with external radius R, internal radius R−d(d<<R), length l and mass M hangs on an insulating cord in a region where there is a homogenous, vertical magnetic field of strength B. It can rotate freely as a whole around its vertical axis, but is constrained, so that it can not move horizontally. The capacitor is charged and there is a voltage difference
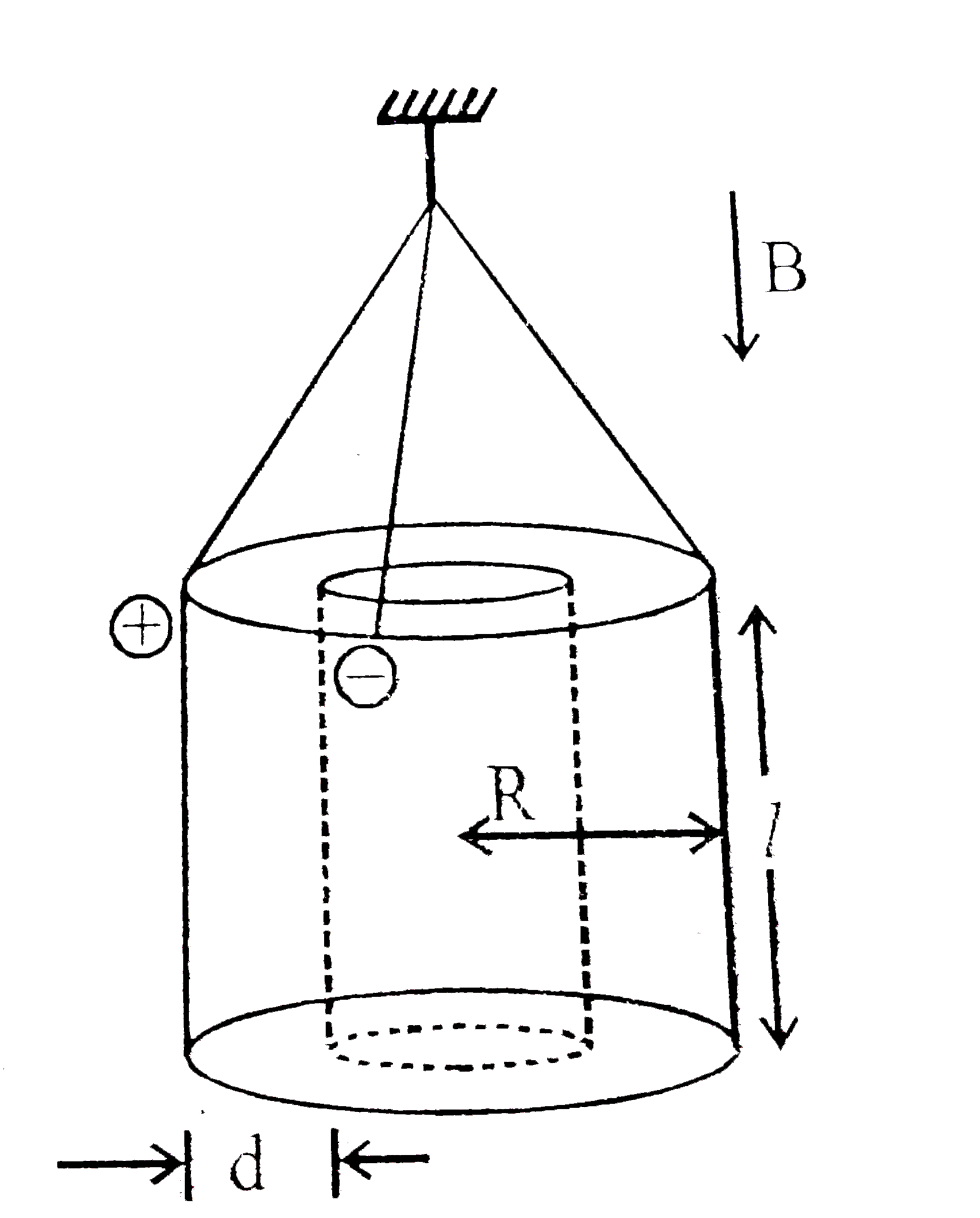
Charge on capacitor is given byA∈02πRlVdB∈0πRlV2dC∈0πRlV3dD∈0πRlV4dA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B. The frequency of revolution is
A3Bq2πmB3Bq2πmC2πm2BqDBq2πm
A charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B the frequency of revolution is
View SolutionIn a spherical capacitor of inner radius a and outer radius 2a dielectric strength of medium is E0 .The maximum potential to which capacitor can be charged is
View SolutionA charge Q is spread uniformly over an insulated ring of radius R.What is the magnetic moment of the ring if it is rotated with an angluar velocity ω about its axis?
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View Solution
