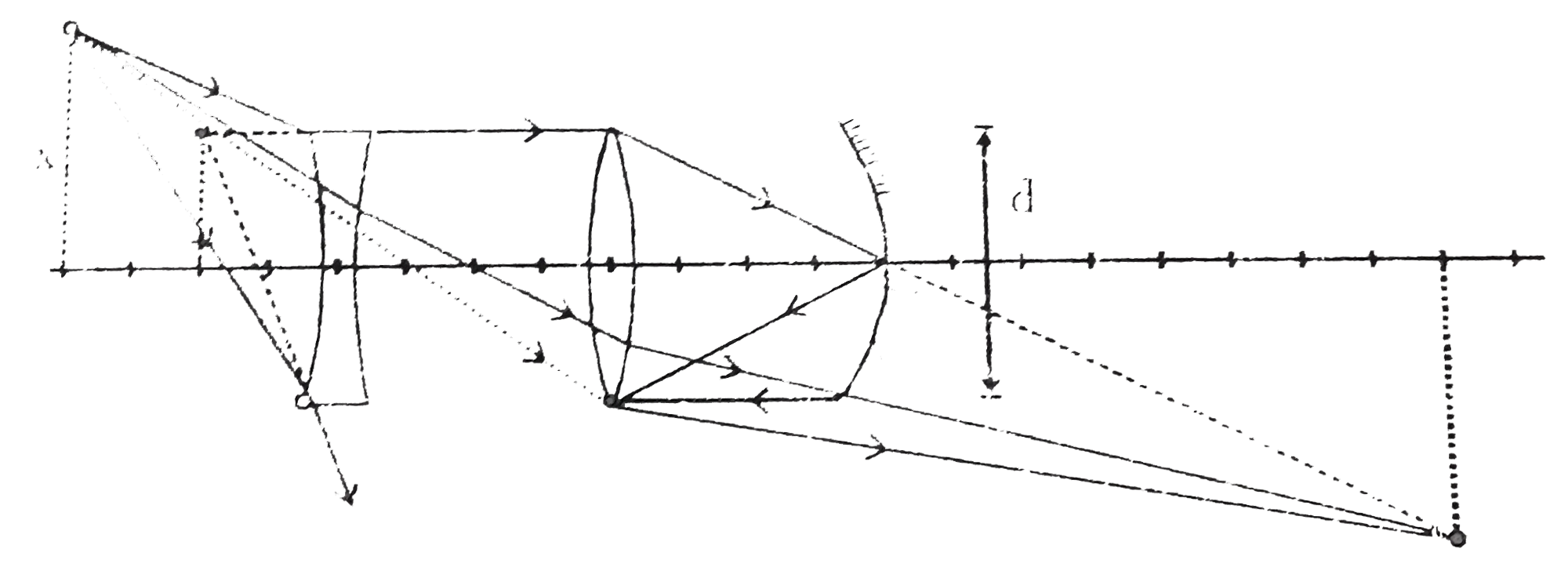
The following objects are placed one after each other in given order onto a central axis with a separation of 40 cm each. A point source of light O. a diverging lens of focal length 40 cm. a converging lens of focal length 40 cm and converging mirror of focal length 80 cm. The aperture diameter of lenses and mirror is d=20 cm. If a point source of light is placed at a perpendicular distance of x from central axis then. (You have to consider single optical event at any optical element)
Mark the CORRECT statement(s):-Solution in Gujrati
Final image is formed in the plane of converging lens
If x>1.5d the rays will not be reflected by converging mirror
For x>d final real images can be captured on a screen after on optical event (i.e refraction or reflection)at every optical system
Final image is real and inverted
The correct Answer is:A, C, D
Let us follow the way the images are formed by the lenses and the mirror. The virtual image formed by the diverging lens has an image distance of
i1=O1f1O1−f1=−4.44−(−4)dm=−2dm (dmrarrdecimeter)
Since the linear magnification is
m1=Hi1HO1=i1O1=12
the height of the first image is
Hi1=x2=HO2.
This virtual image is seen by the diverging lens as an object with an object distance of O2=f2+|i2|=6dm, therefore the image formed by second lens has an image distance of
i2=O2f2O2−f2=6.46−4dm=12dm
The linear magnification of the second lens is
m2=i2O2=126=2
Hence the height of the second image is Hi2=m2HO2=m2Hi1=xc=HO3.
The second image is seen by the concave mirror as a virtual object bering at a distance of O3=f3−i2=−8dm, therefore the image is formed at
i3=O3f3O3−f3=−8.8−8−8=−64−16=1dm
This is a real image and since the linear magnification of the mirror is:
m3=i3O3=12
the height of the final image is
Hi3=m3HO3=x2
Note that final image is formed in the plane of the converging lens, therefore the image can only be captured on a screen if its height is greater than the radius of the lens. This happens when x is greater than d, therefore the list condition for perpendicular is d lt x. If x is increased further than 1.5d, the rays will all pass under the concave mirror and there will be no image formation. Therefore the solution of the problem is :
d<x<1.5d.creased further than 1.5d, the rays will all pass under the concave mirror and there will be no images formation. Therefore the solution of the problem is:
d<x<1.5d.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHS
1 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
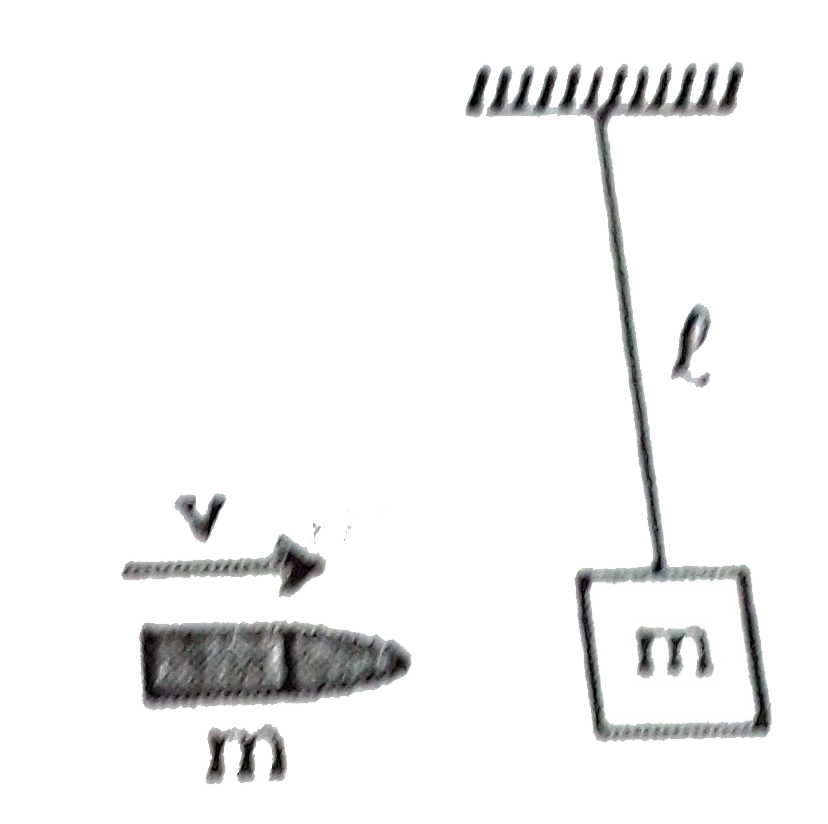
A block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis ?
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View SolutionA parallel beam of rays is incident on a convergent lens with a focal length of 40cm. Where a divergent lens with a focal length of 15cm be placed for the beam of rays to remain parallel after passing through the two lenses.
View SolutionA diverging lens with magnitude of focal length 25cm is placed at a distance of 15cm from a converging lens of magnitude of focal length 20cm. A beam of parallel light falls on the diverging lens. The final image formed is.
View SolutionA converging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed 60 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 50 cm from the lens. Find the locations of the images formed.
View SolutionA converging lens and a diverging mirror are placed at a separation of 20 cm. The focal length of the lens is 30 cm and that of the mirror is 50 cm. Where should a point source be placed between the lens and the miror, so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
View SolutionA diverging lens with magnitude of focal length 25 cm is placed at a distance of 15 cm from a converging lens of magnitude of focal length 20 cm. A beam of parallel light falls on the diverging lens. The final image formed is
View SolutionA diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself ?
View SolutionA converging lens and a diverging mirror are placed at a separation of 15 cm. The focal length of the lens is 25 cm and that of the mirror is 40 cm. Where should a point source be placed between the lens and the mirror so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis ?
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View Solution
