A small particle of mass m is fixed to the perimeter of a ring of same mass and radius r. The system comprising of particle and ring is placed on a horizontal plane. Friction is negligible on horizontal plane. Initially particle is at top most point, then the system is released from rest. Answer next two question when the particle is at the same height as the centre of ring aftr being released from top most point. Assume that the ring stays in vertical plane during its motion under consideration

Mark the CORRECT option(s):Solution in Gujrati
Speed of centre of mass of system is √gr4
Angular velocity of system is ω=√gr
Contact point of ring with ground is instantaneously at rest
Centre of ring is instantaneously at rest
The correct Answer is:A, B, D
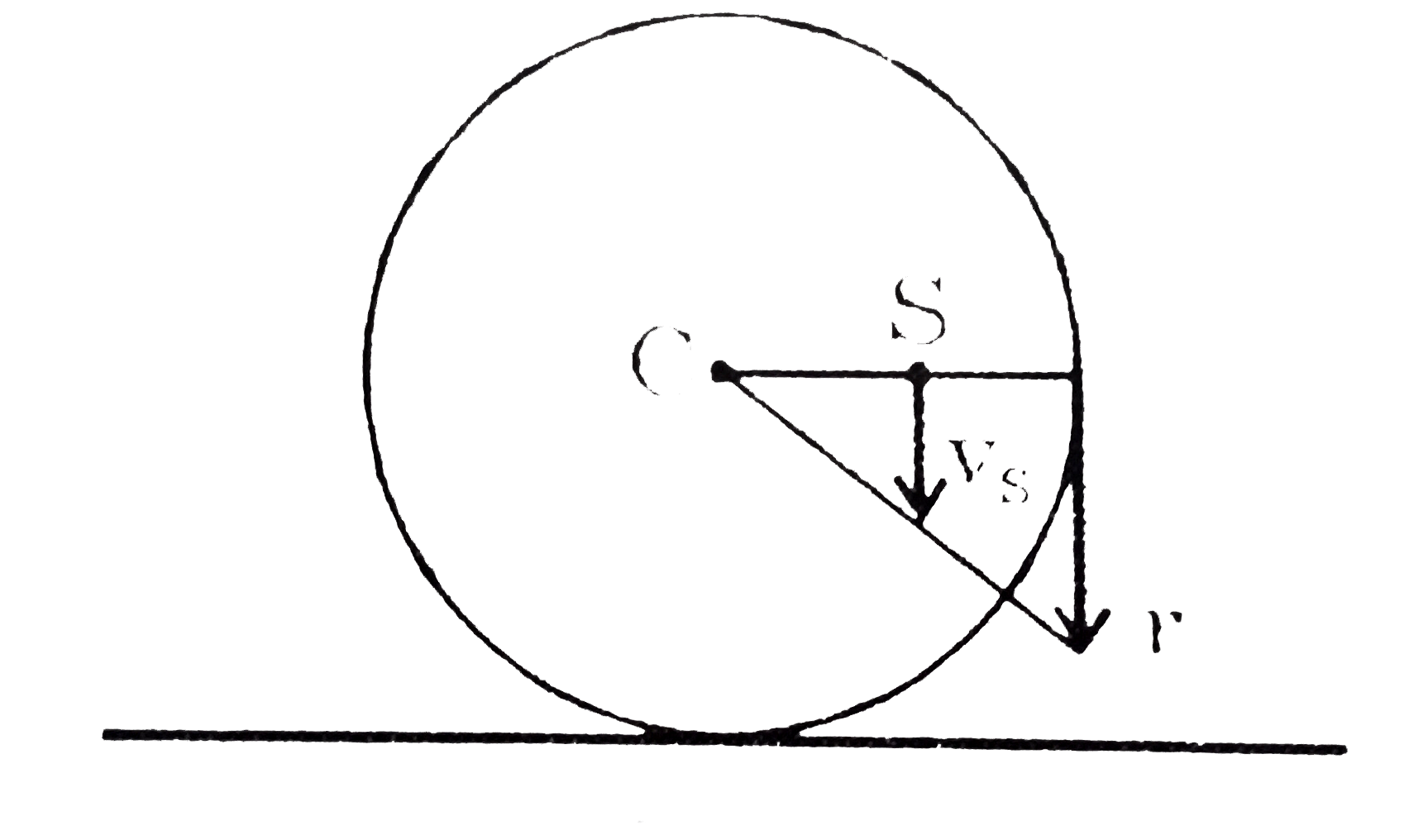
In the absence of horizontal external force centre of mass of system S falls vertically. Since mass of ring and particle are equal their motion about CM of system is symmetrical. At given instant centre of ring will be instantaneous centre
From work energy theorem
mgr=12mv21+12mr2ω2
also v1=rω
thus v1=√gr
|→aC|=|→a1|=v2rel(r/2)=(v1/2)2r/2=g2
[vrel=v1−vS=v12]
At the given instant acceleration of particle is equal to the centripetal acceleration of its rotaion about centre of mass.

N,r2=32mr2α ....(i)
as=r2α ...(ii)
as=2mg−N2m ...(iii)
Thus N=32mg
Topper's Solved these Questions
- TEST PAPERSBook:ALLEN Chapter:TEST PAPERSExercise:PHYSICS
Explore 16 Videos
- TEST PAPERSBook:ALLEN Chapter:TEST PAPERSExercise:MATHS
Explore 1 Video
- TEST PAPERSBook:ALLEN Chapter:TEST PAPERSExercise:part-2 physics
Explore 73 Videos
- TEST PAPER 4Book:ALLEN Chapter:TEST PAPER 4Exercise:PHYSICS
Explore 45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLEN Chapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
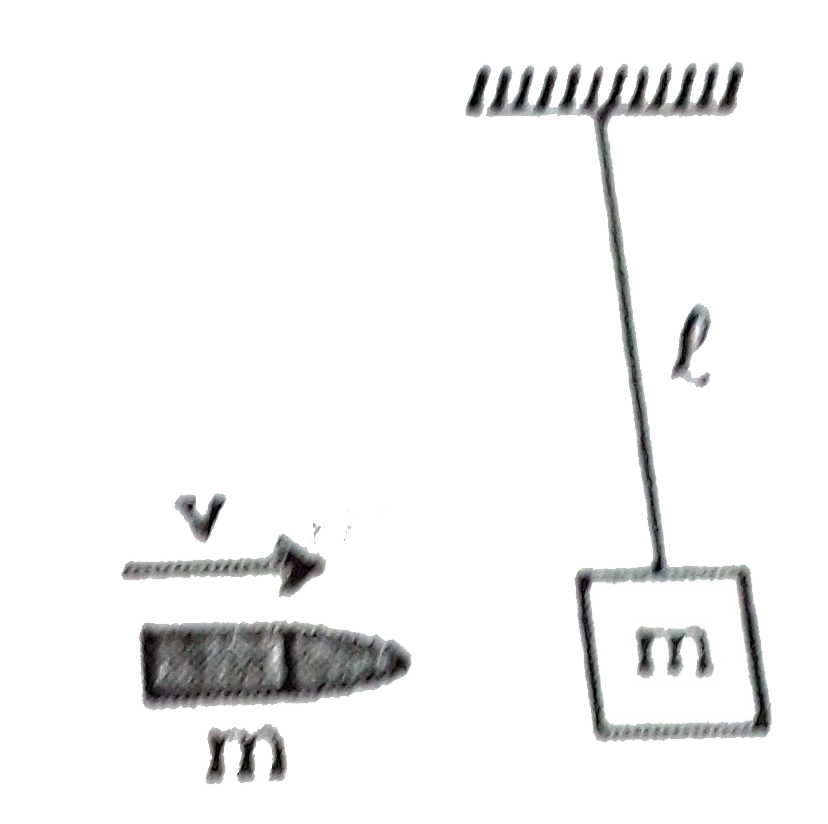
A block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.

View SolutionA particle of mass m is placed at a distance x from the centre of ring along the line through the centre of the ring and perpendicular to its plane. if xlt lta , the particle of mass m will:
View SolutionA particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m and radius 'r' . The system is released from rest and rolls without sliding. The angular release is acceleration of ring just after release after

View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance sqrt(3)a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionA point particle of mass m is released from a distance sqrt(3)R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
View SolutionConsider two identical rings of mass M and radius R fixed on a horizontal axis in a gravity - free space. A particle of mass m is held at rest at the centre of 1^("st") ring and projected along the axis towards 2^("nd") ring. The minimum speed of projection so that the particle reaches the centre of 2^("nd") ring is
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
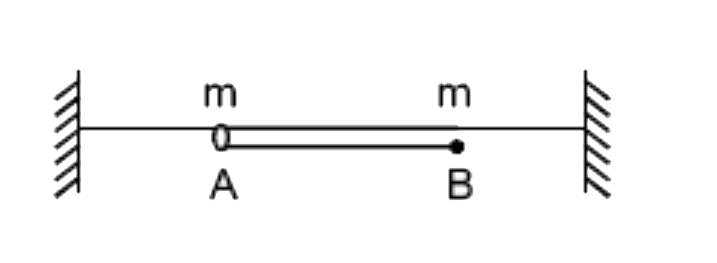
View SolutionA small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is 35, the ring will start sliding when the connecting string will make an angle θ with the vertical, then θ will be (particle is free to move and ring can slide only)
View SolutionA uniform thin circular ring of mass m (m = 0.4 kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.
View Solution
