A uniform ring of mass m and radius R is performing pure rolling motion on a horizontal surface. The velocity of centre of the ring is V0. If at the given instant the kinetic energy of the semi circular are AOB is lambda mv0_(2), then find the value of 11λ(takeπ=227)
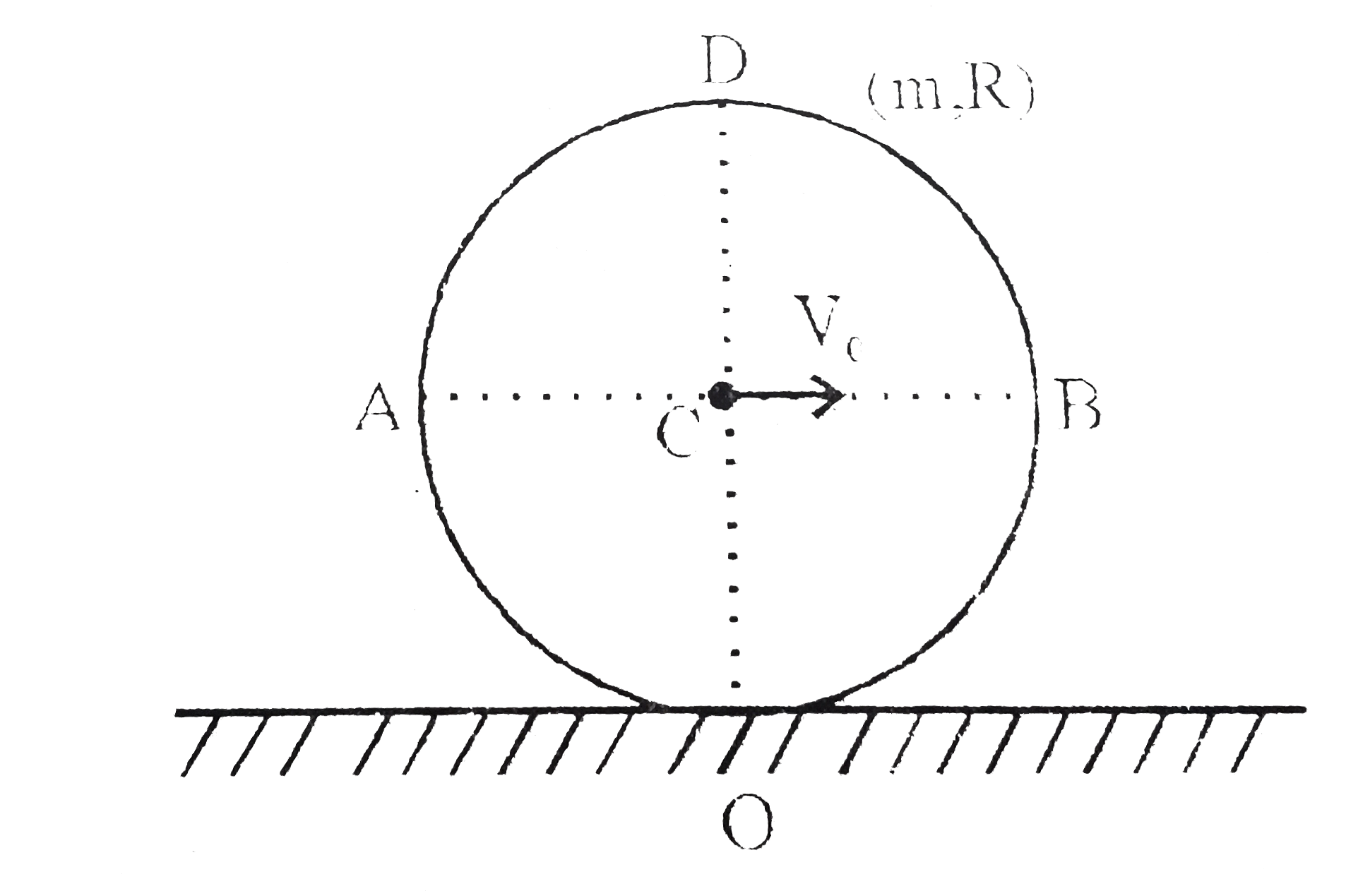 Solution in Gujrati
Solution in Gujrati
The correct Answer is:2
V=2v0sin.θ2dk=12dmv2

K=∫dk
K=∫12M2πRRdθ(2V0sin.θ2)2
=MπV20π/2∫−π2sin2,θ2dθ
=MV20π(π2−1)=MV20(12−1π)
E=211MV20
λ=211
11λ=2
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHS
1 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
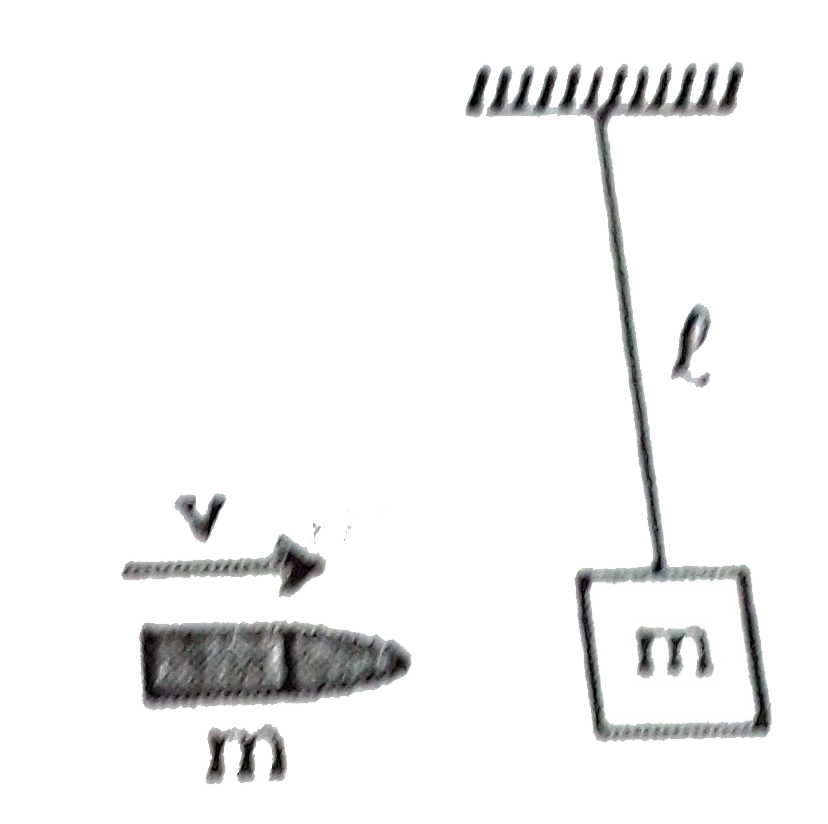
A block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionCentre Of Mass Of Uniform Semi Circular Ring
View SolutionA uniform ring of radius R is given a back spin of angular velocity V_(0)//2R and thrown on a horizontal rough surface with velocity of centre to be V_(0) . The velocity of the centre of the ring when it starts pure rolling will be
View SolutionThe potential energy of interaction between the semi-circular ring of mass M and radius R, and the particle of mass M placed at the centre of curvature of the semi-circular arc is:
View SolutionA ring mass m and radius R has three particle attached to the ring as shown in the figure. The centre of the centre v0. Find the kinetic energy of the system. (Slipping is absent).
 .
.
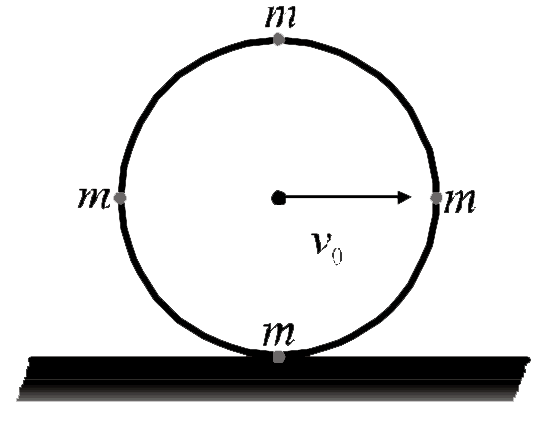
View SolutionA ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
View SolutionA uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V_(0) . The kinetic energy of the segment ABC is:
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
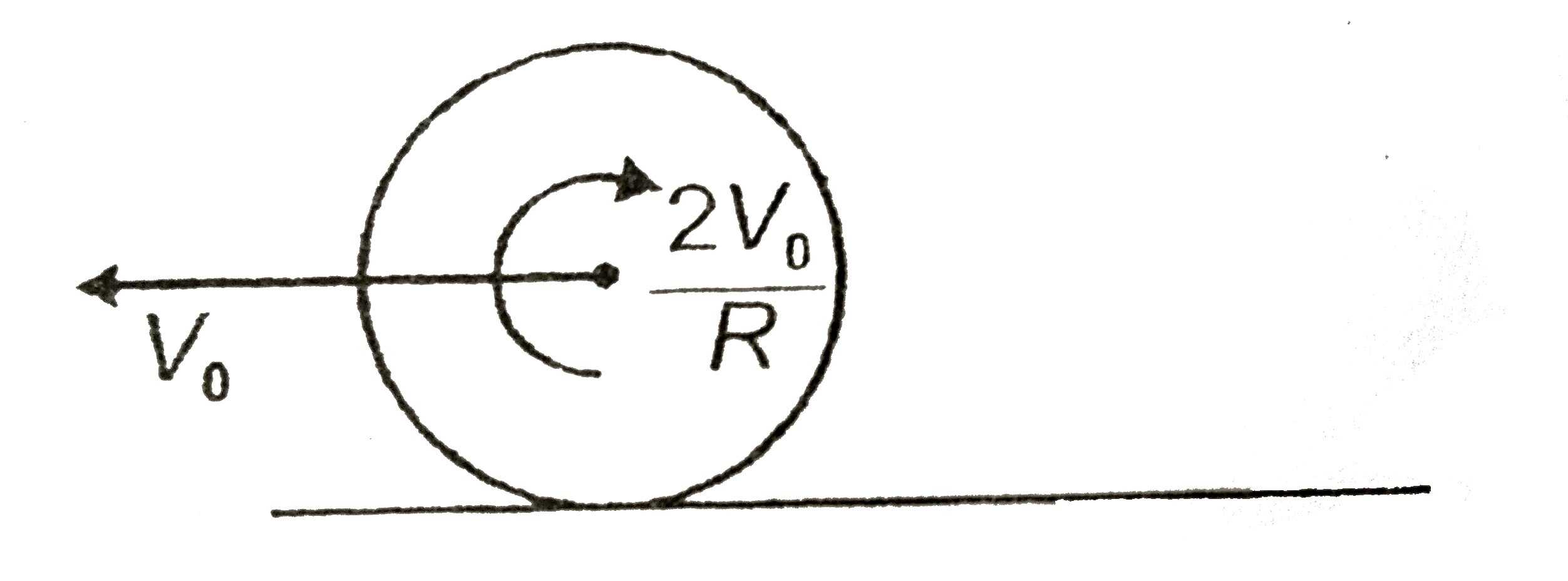
View Solutionकिसी लुढ़कते हुए छल्ले की सम्पूर्ण गतिज ऊर्जा ज्ञात कीजिए, यदि छल्ले का द्रव्यमान, वेग तथा त्रिज्या क्रमशः m,v तथा R हैं।
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v_(0) on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is mu , then work done by the friction in the process is
View SolutionA hollow cylinder of mass m and radius r is kept on a smooth horizontal surface. Horizontal force F is applied at a height above the centre. Find the value of h/R so that ring performs pure rolling on the surface.
View Solution
