A ray of light is incident on the surface of a sphere of refractive index √72 other half of sphere is silvered. After refraction it is reflected and then refracted out of sphere again such that the total deviation is minimum then total deviation of the ray will be (sin410−√37)
 Solution in Gujrati
Solution in Gujrati
1020
980
1360
1630
The correct Answer is:C
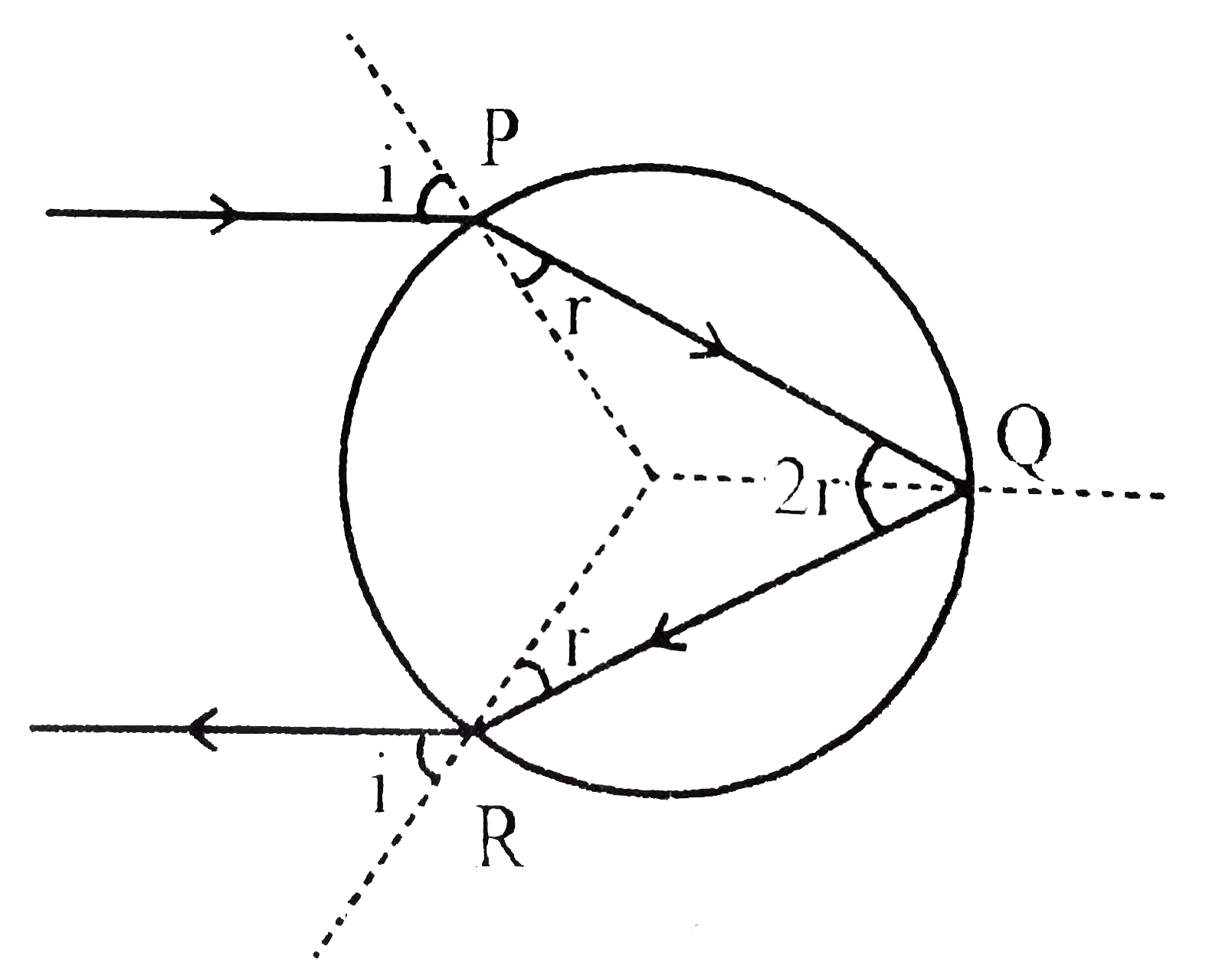
deviation at 'P' =i−r
deviation at 'Q' =π−2r
deviation at 'R' =i-r
Total deviation
δ=2(i−r)+π−2r
=π+2i−4r
for minimum deviation
dδdi=0⇒2−4drdi=0
⇒drdi=12
∴μsinr=sini
μcosrdr=cosidi
drdi=cosiμcosr=12
μ2cos2r=(cos2i)4
μ2(1−sin2r)=4cos2i
μ2(1−sin2iμ2)=4cos2i
⇒cos2i=14
cosi=12
i=60
∴sinr=√37⇒r=410
∴δ=π+2i−4r
=180+2(60)−4(41)
=1360
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHS
1 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
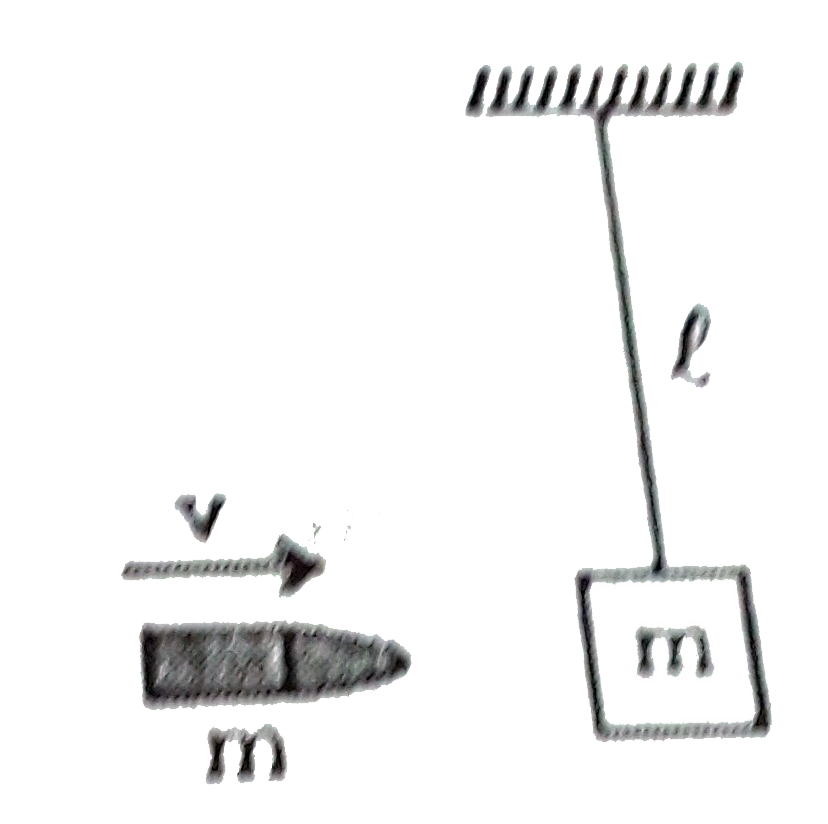
A block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA ray is incident on a glass sphere as shown.The opposite surface of the sphere is partially silvered .If the net deviation of the ray transmitted at the partially silvered surface is 1/3rdof the net deviation suffered by the ray reflected at the partially silvered surface(after emerging out of the sphere).Find the refractive index of the sphere.

View SolutionA ray of light is incident on the surface of a transparent sphere of R.I.μ=√72. After refraction is is internally reflected and refracted out of the sphere as shown in the figure. Find the angle of incidence 'I' so that the total deviation produced is minimum. 'C' is the centre of the sphere.
 .
.
View SolutionA ray is incident on a sphere of refractive index sqrt(2) as shown in figure. Angle of refraction of the ray inside sphere is 30^(@) if total deviation suffered by the ray is 30x^(0) , then find x.
View SolutionA ray incident at a point at an angle of incidence of 60^(@) enters a glass sphere with refractive index sqrt(3) and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA light ray is incident on a transparent sphere of index = √2 , at an angle of incidence =45∘ , What is the deviation of a tiny fraction of the ray, which enters the sphere, undergoes two internal reflections and then refracts out into air?
View SolutionA ray incident at angle of incident 60∘ enters a glass sphere of refractive indec μ=√3. This ray is reflected and refracted at the farther surface of the sphere. The angle between reflected and refracted rays at this surface is
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View SolutionA ray incident at an angle of incidence 60∘ enters a glass sphere of refractive index μ=√3. This ray is reflected and refracted at the further surface of the sphere. The angle between reflected and refracted rays at this surface is
View SolutionA light ray enters a solid glass sphere of refractive index sqrt3 at an angle of incidence 60@ . The ray is both reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is
View SolutionA ray incident at an angle of incidence 60∘ enters a glass sphere of refractive index μ=√3 . This ray is reflected and refracted at the farther surface of the sphere. The angle between reflected and refracted rays at this surface is
View SolutionA ray incident at a point at an angle of incidence of 60∘ enters a glass sphere with refractive index √3 and it is reflected and refracted at the farther surface of the sphere. The angle between the reflected and refracted rays at this surface is:
View Solution
