A parabolic mirror is silvered at inner surface. The equation of the curve formed by its intersection with X-Y plane is given by y=x24. A ray travelling in X-Y plane along line y=x+3 hits the mirror in second quandrant and gets reflected. The unit vector in the direction of reflected ray will be
 Solution in Gujrati
Solution in Gujrati
1√2(−ˆi−ˆj)
1√2(ˆi+ˆj)
−2ˆi−3ˆj√13
−(2ˆi+ˆj)√5
The correct Answer is:A
Point of intersection of two curves
y=x24=x+3
⇒x=−2,x=1
dydx=x2
i.e., (dydx)x=−2=−1
tanβ= slope of incident ray =1
tanβ=1
β=450

tanα=∣∣∣(dydx)x=−2∣∣∣=1
α=450
⌊i=⌊r=0o
Theref≤ctedraymakes45^(o)withX−aξs<br>Then (1)/(sqrt(2))(-hat(i)-hat(j))
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHS
1 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
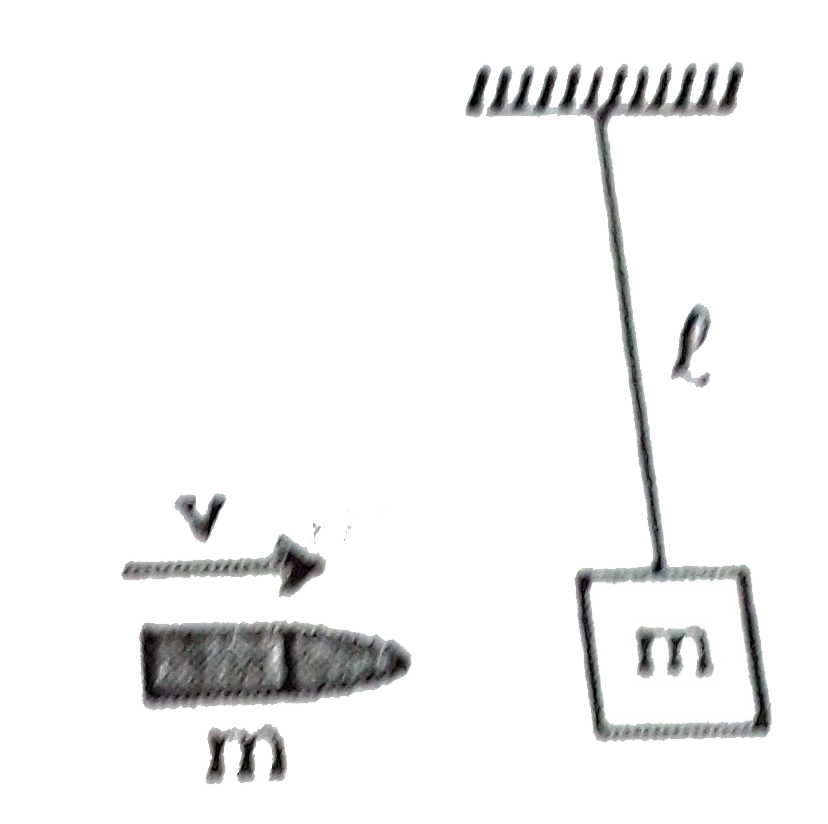
A block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA ray of light travels along a line y=4 and strikes the surface of curves y2=4(x+y). Then the equations of the line along which of reflected ray travels is x=0 (b) x=2 (c) x+y (d) 2x+y=4
View SolutionA wavefront expressed by x + y – z = 4 is incident on a plane mirror which is lying parallel to xy plane. Write a unit vector in the direction of reflected ray.
View SolutionA ray of light in incident along a vector ˆi+ˆj−ˆk on a plane mirror lying in y-z plane. The unit vector along the reflected ray can be
View SolutionA ray of light moving parallel to x-axis gets reflected from a parabolic mirror whose equation is 4(x+y)−y2=0 . After reflection the ray pass through the pt(a,b). Then the value of a + b is
View SolutionIf a ray travelling the line x = 1 gets reflected the line x+y=1 then the equation of the line along which the reflected ray travels is
View SolutionA ray of light travels along the line 2x−3y+5=0 and strikes a plane mirror lying along the line x+y=2. The equation of the straight line containing the reflected ray is
View SolutionA ray of light travels along a line y=4 and strikes the surface of curves y2=4(x+y). Then the equations of the line along which of reflected ray travels is x=0 (b) x=2 (c) x+y (d) 2x+y=4
View SolutionTwo plane mirrors are combined to each other such that one is in y-z plane and the other is in X-z plane. A ray of light travelling along a vector ˆi+ˆi+ˆk is incident on the first mirror. Find the unit vector in the direction of emergent ray after successive reflections through both the mirrors.
View SolutionIf a ray travelling the line x = 1 gets reflected the line x+y=1 then the equation of the line along which the reflected ray travels is
View SolutionA ray of light travelling along the line 2x−3y+5=0 ,after striking a plane mirror lying along the line x+y−2=0 gets reflected then equation of the reflected straight line is
View SolutionIf a ray travelling the line x=1 gets reflected the line x+y=1, then the equation of the line along which the reflected ray travels is
View Solution
