A heavy and a light cylindrical rollers of diameter D and d respectively rest on a horizontal plane as shown. The larger roller has a string wound around it to which a horizontal force 'P' can be applied as shown. Assuming 'mu' (coefficient of friction) is same at all surfaces of contact, find the critical value of 'mu' such that larger roller can be just pulled over smaller one.
 Solution in Gujrati
Solution in Gujrati
μ=√Dd
μ=2√Dd
μ=√dD
μ=2√Dd
The correct Answer is:C
sinα=D−dD+d
cosα=2√DdD+d
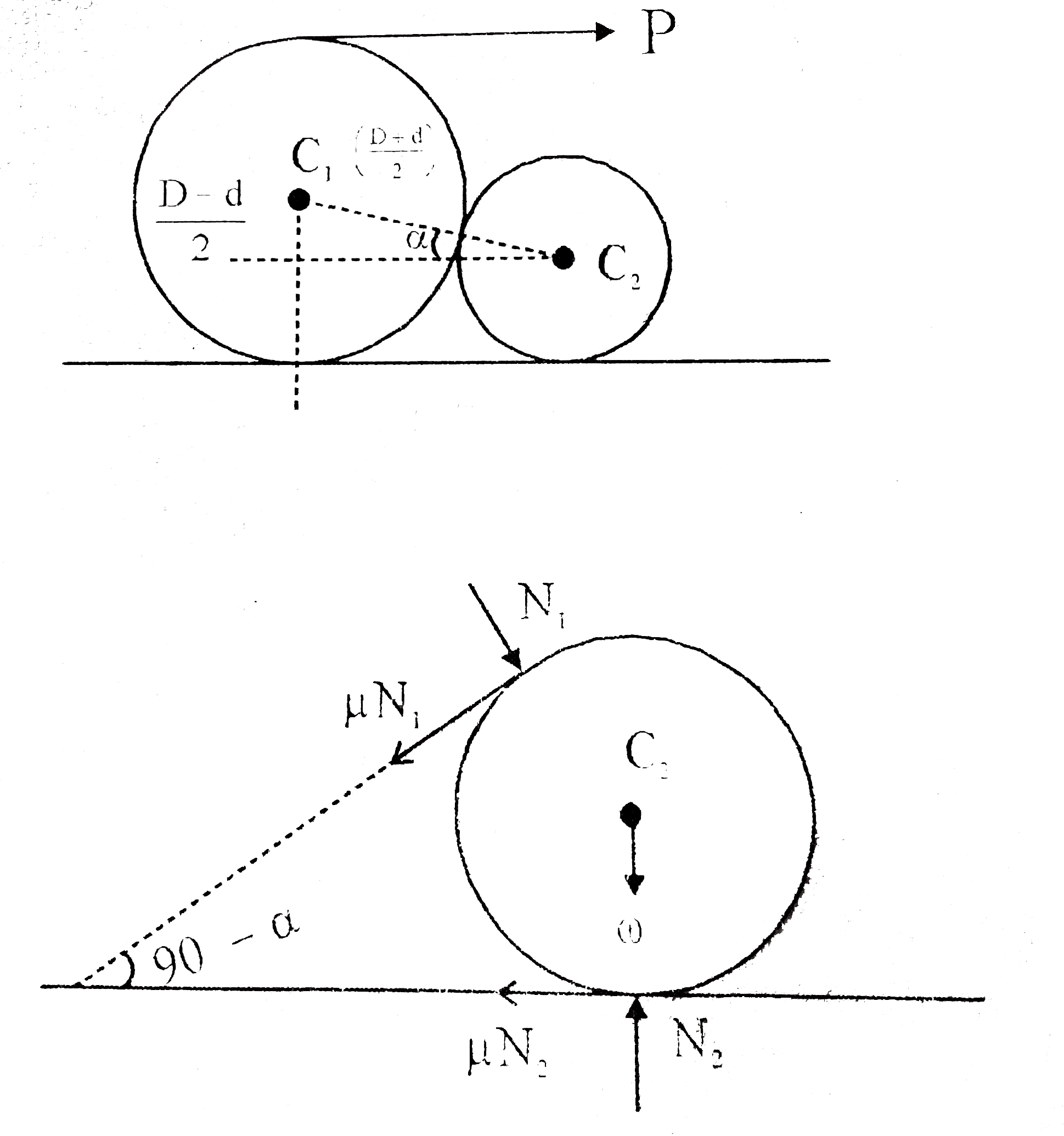
If smaller cylinder neither rolls nor slides then larger cylinder can be pulled over it. Then sum of moments about C2 should be zero
μN1d=μN2d
N1=N2
for no sliding
μN2+μN1cos(90−α)=N1cosα
⇒μ(1+sinα)=cosα
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHS
1 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
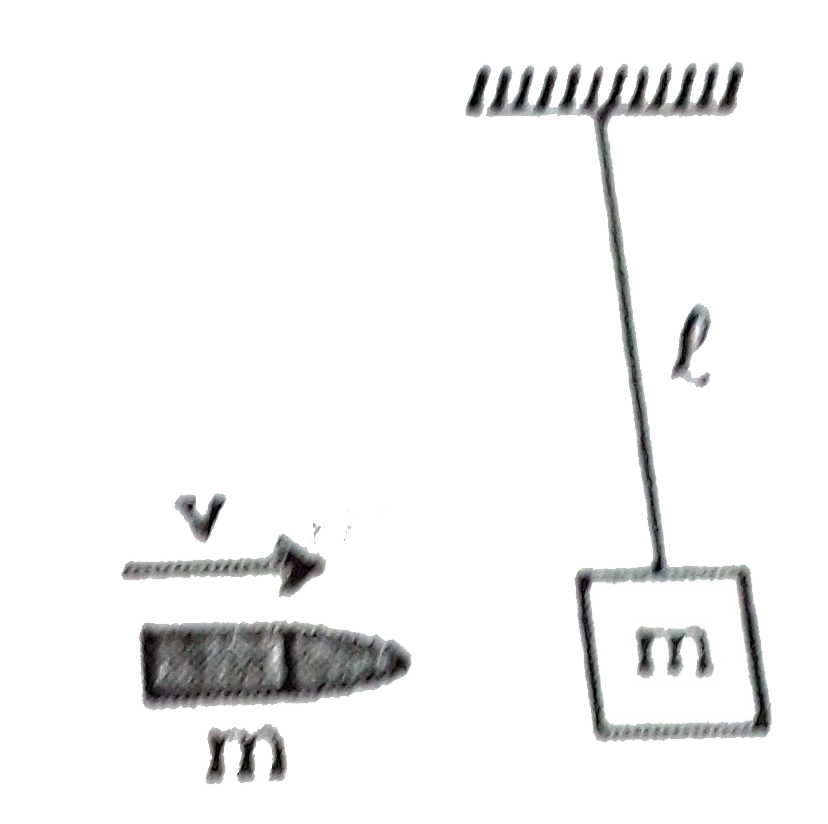
A block of mass m is hanging from a light string of length l . A bullet of mass m strikes the hanging mass and gets embedded into it. The value of v such that tension in string and the speed of combined mass becomes zero simultaneously during the subsequent motion , is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionConsider two heavy right circular rollers of the radii R and r respectively and rest on a rough horizontal plane a shown in figure. The larger roller has a string wound around it to which a horizontal force P can be applied as shown. Assuming that the coefficient of friction m has the same value for all surfaces of contact, determine the necessary condition under which the larger roller can be pulled over the smaller one. Assume the smaller cylinder should neither roll nor slide.
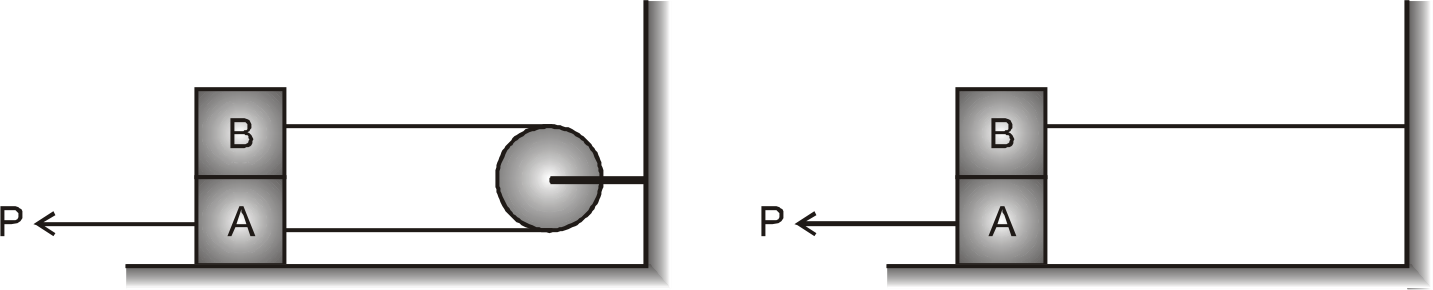
View SolutionEach of the two block shown in the figure has mass m. The pulley is smooth and the coefficient of friction for all surfaces in contact is μ. A constant horizontal force P applied in two cases shown in such a way that block A start just sliding then the value of minimum force P in case-I and case-II is :
View SolutionA roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
View SolutionFind the acceleration of slid right circular roller A , weighing 12kg when it is being pulley by another weight B (6 kg) along the horizontal plane as in figure ( pulley in massless ) . The weight B is attached to the end of a string wound around the circularference of roller. Assume there is no slipping of the roller and the string is inextensible.
View SolutionA heavy and a light cylindrical rollers of diameter D and d respectively rest on a horizontal plane as shown. The larger roller has a string wound around it to which a horizontal force 'P' can be applied as shown. Assuming 'mu' (coefficient of friction) is same at all surfaces of contact, find the critical value of 'mu' such that larger roller can be just pulled over smaller one.
View SolutionA small roller coaster starts at point A with a speed u on a curved track as shown in the figure The friction between the roller coaster and the track is negligible and it always remains in contact with the track. The speed of roller coaster at point D on the track will be
View SolutionA solid cylindrical roller of mass M and radius R is rolled on a rough horizontal surface by applying a horizontal force F at the top most point. The frictional force between the roller and the surface, is
View Solution(A) : It is easier to pull a lawn roller than to push on the same horizontal rough surface
(R ) : Pulling body decreases normal reaction
View SolutionA block of mass m is pulled along a horizontal surface by applying a force at an angle θ, with the horizontal. If the block k travels with a uniform velocity and has a displacement d and the coefficient of friction is μ. Then find the workdone by the applied force?
View SolutionA roller of mass 300 kg rests against a step of height 20 cm. If radius of the roller is 50 cm find the minimum horizontal force to be applied passing through its center of mass to take the roller on to the step.
View SolutionA roller of mass 300kg rests against a step of height 20 cm. If the radius of the roller is 50 cm find the minimum horizontal force to be applied passing through its center of mass to take the roller on to the step.
View Solution
