A particle of mass m carrying charge is revolving around a fixed charge in a circular path of radius r. Calculate the period of revolution.Solution in Gujrati
or
where is the vector drawn from source charge is test charge.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
For spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
View SolutionA stone is dropped into a quiet lake and waves move in circles speading out radially at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8cm, how fast is the enclosed area increasing?
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
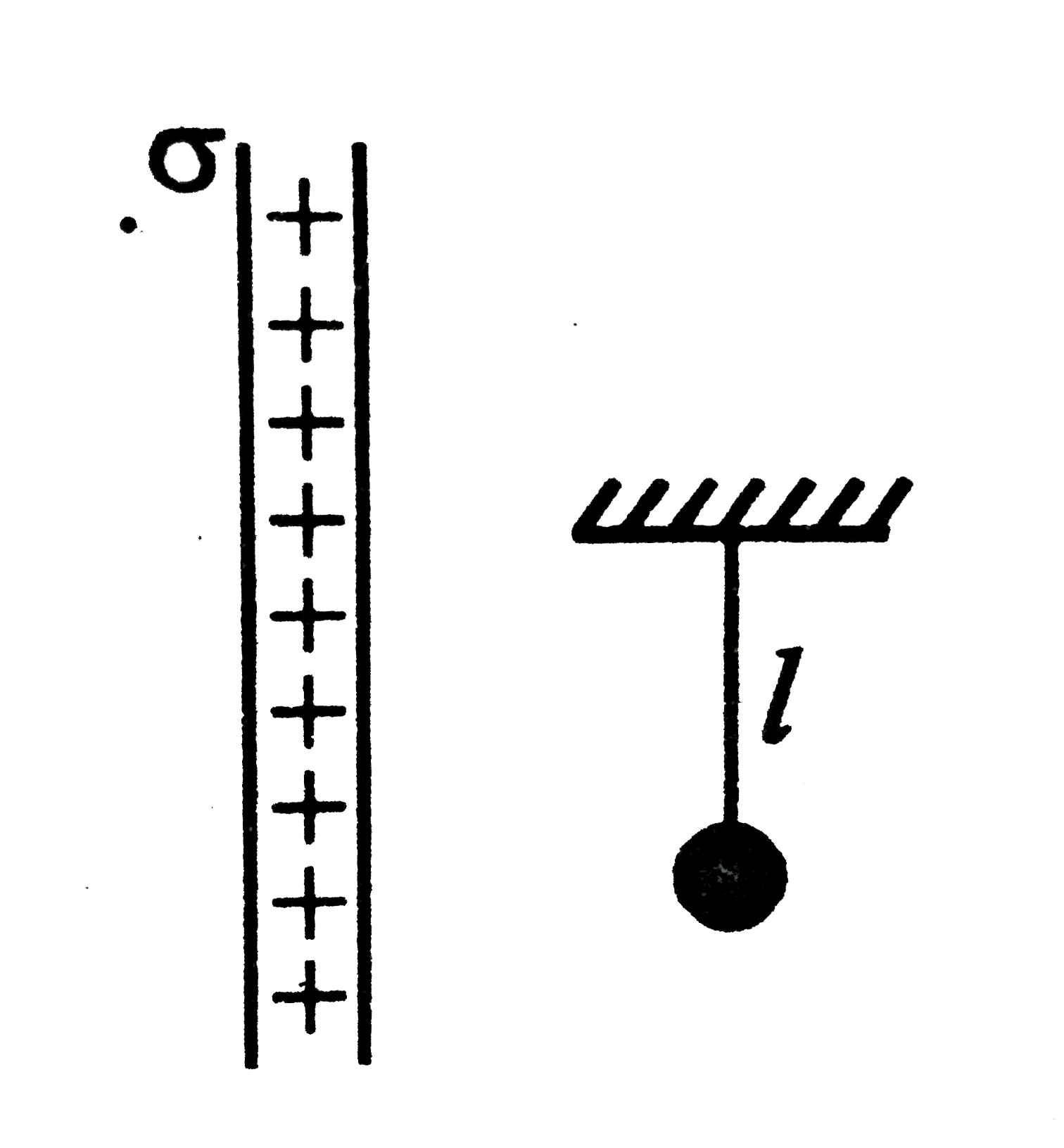 .
.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA particle of mass m and carrying charge -q_(1) is moving around a charge +q_(2) along a circular path of radius r period of revolution of the charge -q_(1) about +q_(2) is
View SolutionThe work done in carrying a charge Q_(1) once round a circle of radius R with a charge Q_(2) at the centre is
View SolutionA particle of mass m_(2) carrying a charge Q_(2) is fixed on the surface of the earth .Another particle of mass m_(1) and charge Q_(1) is positioned right above the first one at an altitude h( ltlt R) .R is radius of earth ,the charge Q_(1) and Q_(2) are of same sign ,then the magnitude of charge Q_(2) at which the velocity of m_(1) at an altitude h_(2) is zero is given by
View SolutionA particle of mass m carrying charge '+q_(1)' is revolving around a fixed charge '-q_(2)' in a circular path of radius r. Calculate the period of revolution.
View SolutionCharge q2 of mass m revolves around a stationary charge q1 in a circulare orbit of radius r. The orbital periodic time of q2 would be
View SolutionA charged particle of mass m1 and charge q1 is revolving in a cricle of radius r. another charged particle of charge q2 and mass m2 is situated at the centre of the circle. If the velocity and time period of the revolving particle be v and T respectively, then,
View SolutionA charged particle of mass m1 and charge q1 is revolving in a circle of radius r .Another charged particle of charge q2 and mass m2 is situated at the centre of the circle.If the velocity and time period of the revolving particle be v and T respectively then
View SolutionA particle of charge q1 and mass m is revolving around a fixed negative charge of magnitude q2 in a circular path of radius r. Find the time period of revolution.
View SolutionCharge q_(2) is at the centre of a circular path with radius r. work done in carrying charge q_(1) once around this equipotential path , would be
View SolutionR त्रिज्या के वृत्त के केन्द्र पर Q2 आवेश रखा है, इसके चारो ओर q1 आवेश को घुमाने में किया गया कार्य है।
View Solution
