Let →a,→b,→c be vectors of length 3,4,5 respectively. Let →a be perpendicular to →b+→c,→b to →c+→a and →c to →a+→b. Then ∣∣→a+→b+→c∣∣ is :Solution in Gujrati
2√5
2√2
10√5
5√2
The correct Answer is:D
∣∣→a+→b+→c∣∣=√a2+b2+c2+2(→a.→b+→b.→c+→c.→a)
∵→a.(→b+→c)=0,→b.(→c+→a)=0 & →c.(→a+→b)=0
⇒→a.→b+→b.→c+→c.→a=0
⇒∣∣→a+→b+→c∣∣=√a2+b2+c2=√32+42+52=5√2
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
20 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Two parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
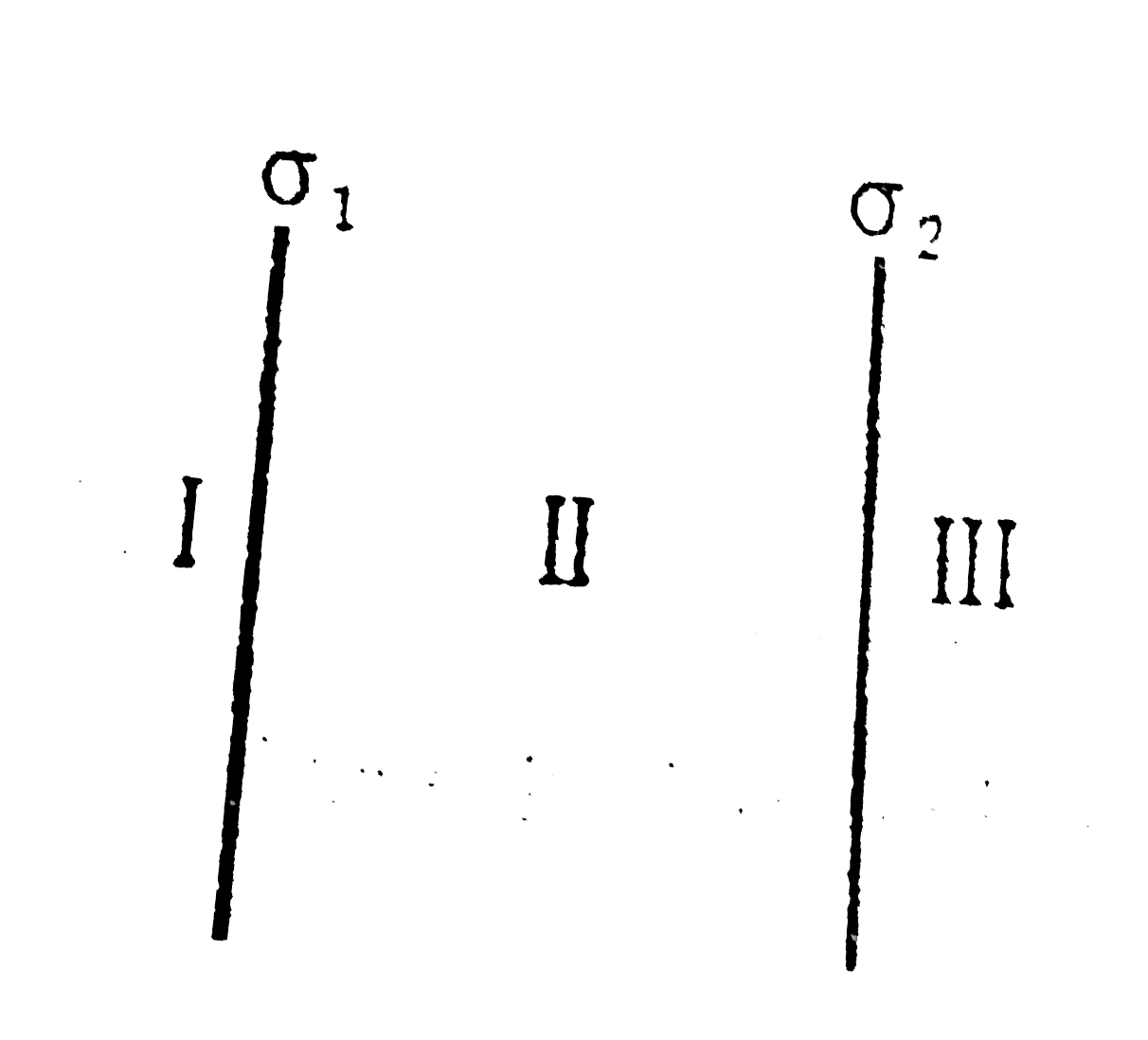
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIn each situation of Column-I two elelctric dipoles having moments →p1 and →p1 of same magnitude (that is ,p1=p2) are placed on x-axis symmetrically about origin in different orientations as shown. In column-II certain inferences are drawn for these two dipoles. Then match the different orientations of dipole in column-I with the corresponding result in column-II.

View SolutionPlanck's constant has dimensions …………….
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionLet vec a,vec b and vec c are vectors of magnitude 3,4,5 respectively.If vec a is perpendicular to vec b+vec c,vec b is perpendicular to vec c+vec a and vec c is perpendicular to vec a+vec b then find the magnitude of vec a+vec b+vec c
View SolutionLet →a,→b,and→c are vectors such that |→a|=3,∣∣→b∣∣=4and|→c|=5,and(→a+→b) is perpendicular to →c,(→b+→c) is perpendicular to →aand(→c+→a) is perpendicular to →b. Then find the value of ∣∣→a+→b+→c∣∣ .
View SolutionIf vec a, vec b, vec c are three mutually perpendicular vectors such that | vec a | = | vec b | = | vec c | then (vec a + vec b + vec c) * vec a =
View SolutionLet vec a,vec b,vec c be vectors with lengths 3,4,5 respectively.Let vec a be perpendicular to vec b+vec c,vec b be perpendicular to vec c+vec a and vec c be perpendicular to vec a+vec b Tehn find the value of |vec a+vec b+vec c|
View SolutionIf vec a,vec b and vec c are vectors such that vec b and vec c are perpendicular,but vec a and vec b are not. Let m be areal number.If vec x*vec a=m,vec x xxvec b=vec c then
View SolutionLet →a,→band→c are three vectors such that |→a|=3,∣∣→b∣∣=3,|→c|=2.∣∣→a+→b+→c∣∣=4and→a is perpendicular to →b,→c makes angle θandϕ with →aand→b respectively, then cosθ+cosϕ=
View SolutionLet →a,→b,→c be vectors of length 3,4,5 respectively. Let →a be perpendicular to →b+→c,→b to →c+→a and →c to →a+→b. Then ∣∣→a+→b+→c∣∣ is :
View SolutionLet →a,→b,→c be non-coplanar vectors and →p=→b×→c[→a→b→c],→q=→c×→a[→a→b→c],→r=→a×→b[→a→b→c].
What is the value of
(→a−→b−→c).→p+(→b−→c−→a).→q+(→c−→a−→b).→r ?
View SolutionLet →a,→b,→c be vectors of length 3,4,5 respectively. Let →a be perpendicular to →b+→c,→b to →c+→a and →c to →a+→b . Then ∣∣→a+→b+→c∣∣.
View SolutionLet →a,→b,→c are three vectors , such that →a+→b+→c=→0 .If ,|→a|=3,∣∣→b∣∣=4 and
|→c∣=5 , then the value of,∣∣→a+→b∣∣2+∣∣→b−→c∣∣2+|→c+→a|2, equal to :
View SolutionLet →a,→b,and→c are vectors such that |→a|=3,∣∣→b∣∣=4and|→c|=5,and(→a+→b) is perpendicular to →c,(→b+→c) is perpendicular to →aand(→c+→a) is perpendicular to →b. Then find the value of ∣∣→a+→b+→c∣∣ .
View Solution
