An accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.
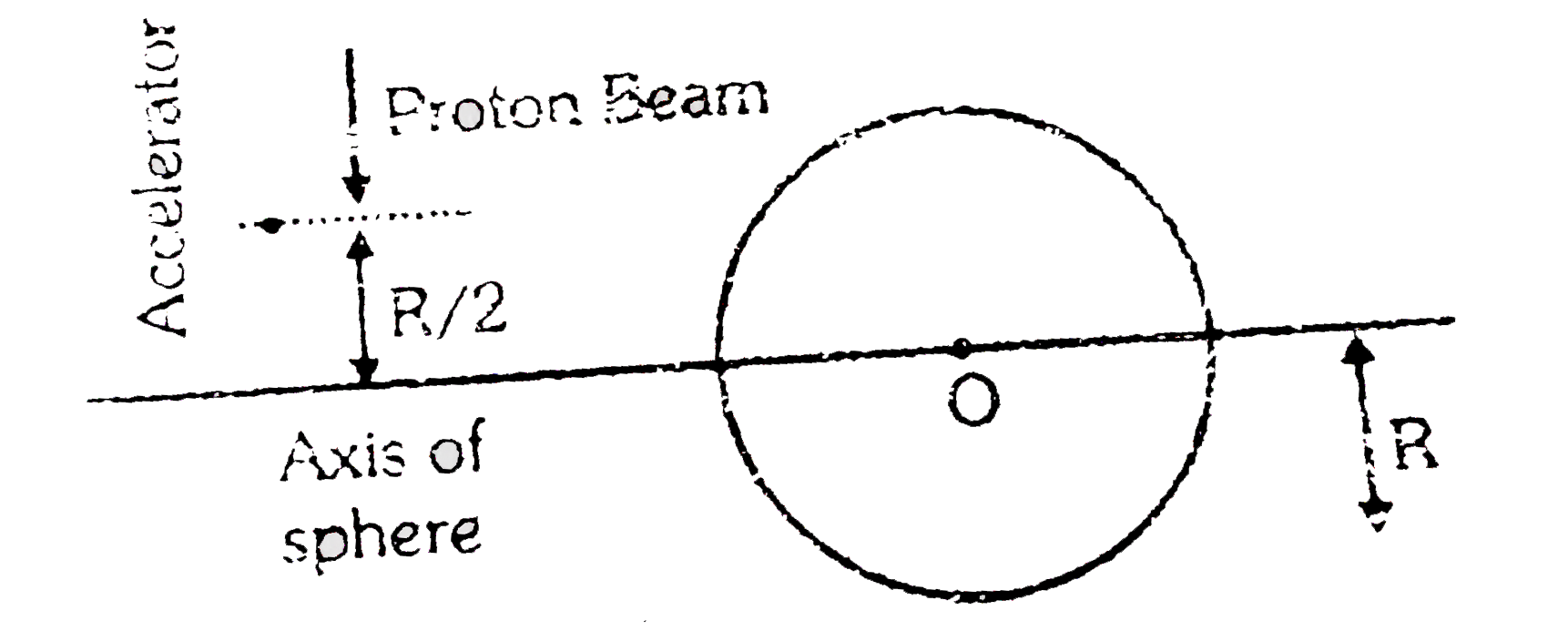
The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given bySolution in Gujrati
v0
v0/2
2v0
None of these
The correct Answer is:B
From the angular momentum conservation
mv0×R2=mv×R⇒v=V02
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 6
3 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Comprehension 7
3 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-07
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
The sketch below show cross section so equipotential surfaces between two charged.Conductors that are shown in solid black.Some points on the equipotenital surfaces .near the conductors are marked as A,B,C….. The arrangements lies in air (Take ε0=8.85×10−12C2/Nm2]
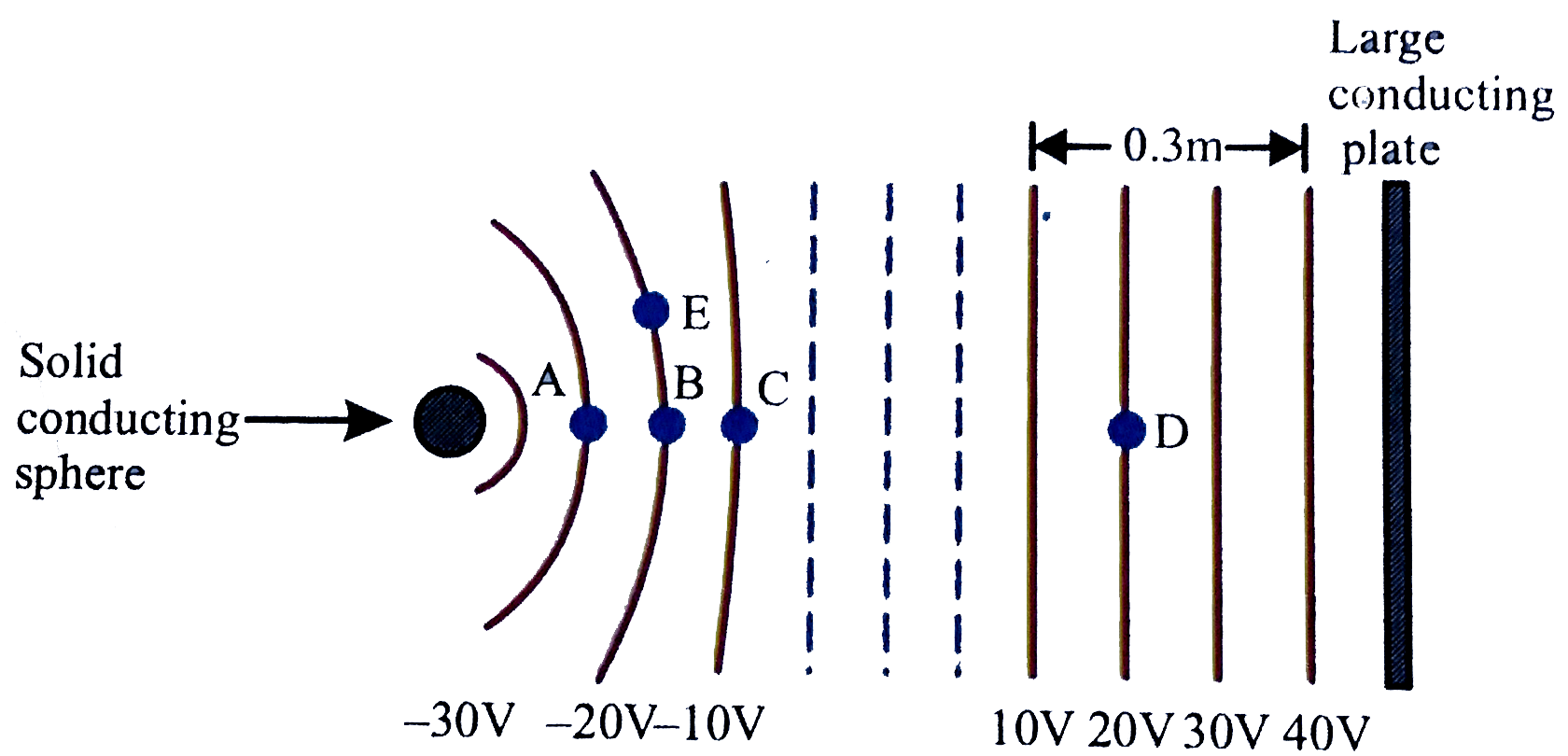
Surfaces charge density of the plate is equal to
View SolutionThe method of electrical images is used to solve the electrostatic problems, where charge distribution is not specified completely. The method consists of replacement of given charge distribution by a simplified charge distribution or a signal point charge or a number of point charges [rovided the original boundary conditions are still satisfied. For example consider a system consider a system containing a point charge q placed at a distance d of form an infinite conducting plane. The boundary conditions are :
(i) Potential is zero at infinity (ii) Potential is zero at each point on the conducting plane If we replaced the conducting plane by a point charge (-q) placed at a distance 'd' opposite to conducting plane. The charge (-q) is called the electrical image.
Now system consists of two charge +q an -q at seperation2d. If charge +q moves to a distance 'y' from the boundary of conducting plane (now absent), the electrical image -q also moves to the same 'y' from the boundary of conducting plane, so that the new distance between +q and -q is 2y

The force between point charge +q and earthed conducting plane is
View SolutionColumn-I shows different charge distributions. Cloumn-II gives corresponding electric dipole moments.
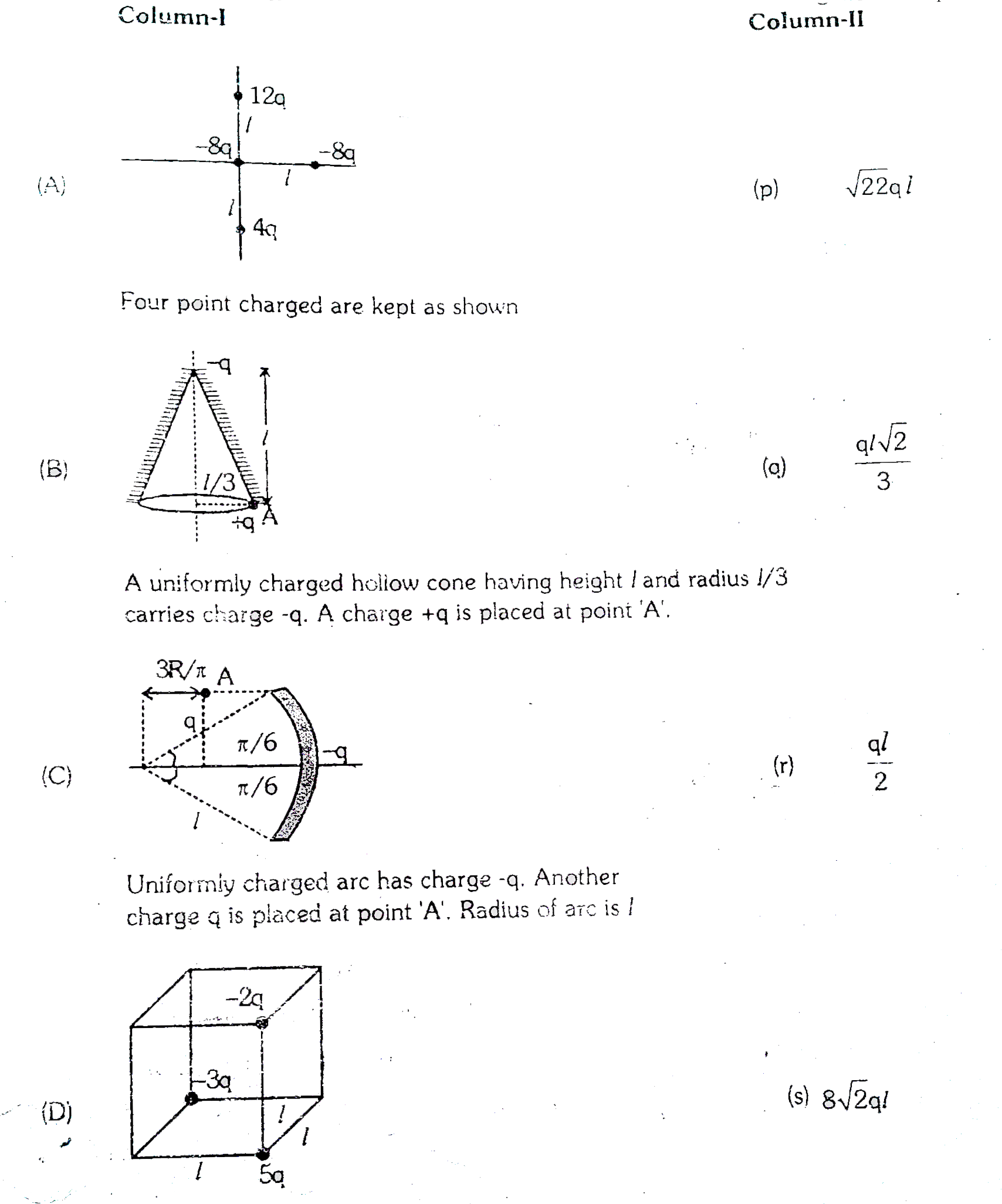
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA perfectly reflecting solid sphere of radius r is kept in the path of a parallel beam of light of large aperture. If the beam carries an intensity I, find the force exerted by the beam on the sphere.
View SolutionA narrow parallel beam of light is incident on a transparent sphere of refractives indexnif the beam finally gets focussed at a point situated at a distance=2×(radius of sphere) form the center of the sphere then findn?
View SolutionNon-relativistic protons accelerated by a potential difference U from a round beam with current I . Find the magnitude and direction of the Poynting vector the beam at a distance r from its axis.
View SolutionA proton accelerator produces a narrow beam of protons, each having an initial speed of v_0 . The beam is directed towards an initially uncharged distant metal sphere of radius R. The sphere is fixed and centered at point O. The initial path of the beam is at a distance of (R/2) from the centre, as indicated in the diagram. The protons in the beam that collide with the sphere get absorbed and cause it to become uniformly charged. The subsequent potential field at the accelerator due to the sphere can be neglected. Assume the mass of the proton as m_P and the charge on it as e. (a) After a long time, when the potential of the sphere reaches a constant value, sketch the trajectory of proton in the beam. (b) Once the potential of the sphere has reached its final, constant value, find the minimum speed v of a proton along its trajectory path. (c) Find the limiting electric potential of the sphere.
View SolutionA beam of electrons and protons move parallel to each other in the same direction, then they
View SolutionThere is a parallel beam of light of larger aperture . Let I be the intensity of light . Perfectly reflecting sphere of radius r is kept in the path of this parallel beam . Find the force exerted by the light beam on sphere .
View SolutionThe initial shape of the wavelenght of the beam is
View SolutionA proton beam is fired from west to east and an electron beam is fired parallel to it in the same direction. Force on the electron beam will be
View Solution30 cm व्यास का धुप रिकार्ड करने वाला गोला (sunshine recorder globe), μ=1.5 अपवर्तनांक वाले काँच का बना है | एक किरण, अक्ष के समान्तर गोले में प्रवेश करती है | गोले के केन्द्र से स्थिति निकालें जहाँ किरण, अक्ष को काटती है |
View Solutionएक इलेक्ट्रॉनों की बीम और एक प्रोटॉनों की बीम एक दूसरे के समान्तर चलती हैं। फिर वे
View SolutionAn electron beam and a proton beam are moving in the same direction parallel to each other. Then it
View Solution
