two concentric rings of radii r and 2rare placed with centre at origin. Tow charges +q each are fixed at the diametrically opposite points of the rings as shown in figure . Smaller ring is now rotated by an angle 90∘ about Z-axis then it is again rotated by 90∘ about Y-axis . Find the work done by electrostatic forces in each step . If finally larger ring is rotated by 90∘ about X-axis , find the total work required to perform all three steps .
 .Solution in Gujrati
.Solution in Gujrati
The correct Answer is:Wfirst step=(83−4√5)Kq2r,Wsecond step=0,Wtotal=0
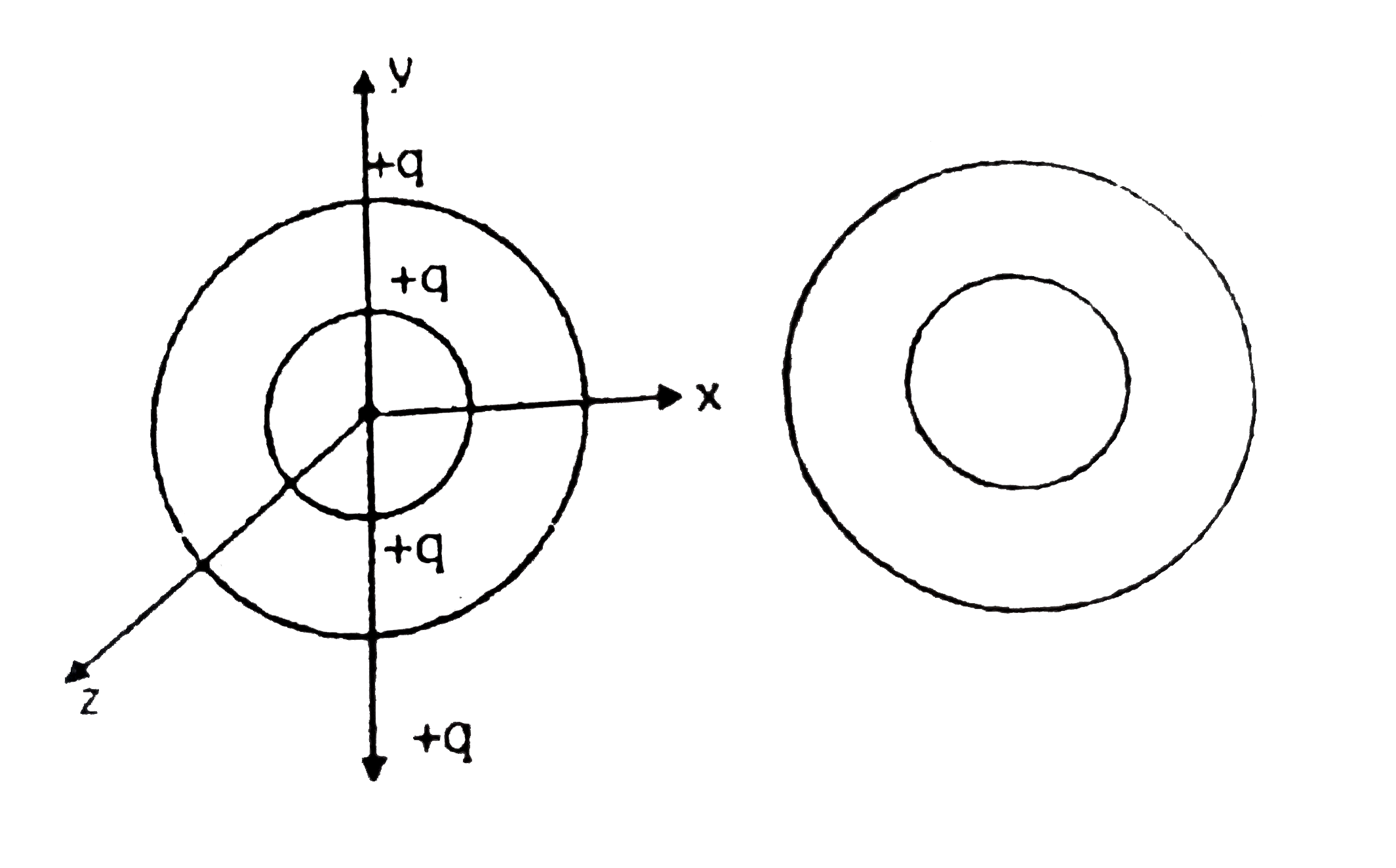
P.E. of outer ring charges does not change
=Kq2R×2+Kq23R×2=8Kq23R,Uf=Kq2√5R×4
Hence Welectron=−ΔU
Welectron=−(Vf−Vi)=−Kq2R[4√5−83]=Kq2R[83−4√5]
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)
35 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[A]
34 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
On moving a charge of 20 coulomb by 2cm, 2J of work is done , the potential difference between the points is .
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionThree particles, each of mass m and carrying a charge q each, are suspended from a common point by insulating mass-less strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA ring of mass m and radius r has a particle of mass m attached to it at a point A. the ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring is released from rest when AB is horizontal. find the angular veloicity and the angular acceleration of the body when AB has turned through an angle (pi)/(3) .
View Solutiontwo concentric rings of radii r and 2r are placed with centre at origin. Tow charges +q each are fixed at the diametrically opposite points of the rings as shown in figure . Smallerring is now rotated by an angle 90^@ about Z-axis then it is again rotated by 90^@ about Y-axis . Find the work done by electrostatic forces in each strop . If finally larger ring is rotated by 90^@ about X-axis , find the total work required to perform all three steps . .
View SolutionTwo square of sides a and 2a are placed in xy plane with their centers at the origin. Two charges, – q each, are fixed at the vertices of smaller square (lying on X axis). Two charges, Q each, are fixed at the vertices of bigger square on the X axis (see figure). (a) Find work required to slowly move the larger square to infinity from the position shown. (b) Find work done by the external agent in slowly rotating the inner square by 90^(@) about the Y axis followed by a rotation of 90^(@) about the Z axis.
View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge q_(0) , is now placed at the centre of the ring. Find the increment in-the tension in ring.
View SolutionA current carrying wire is placed along the axis of a uniformly charged circular ring. If the ring starts rotating about its central axis what will be force on the current carrying wire due to the moving charges of ring.
View SolutionA charge Q is spread uniformly over an insulated ring of radius R .What is the magnetic moment of the ring if it is rotated with an angluar velocity omega about its axis?
View SolutionA short dipole is placed on the axis of a uniformly charged ring (total charge -Q, radius R) at a distance R√2 from centre of ring as shown in figure. Find the Force on the dipole due to that ring

View SolutionThe moment of inertia of a ring about an axis passing though the centre and perpendicular to its plane is l. It is rotating ring is gently placed omega Another identical ring is gently placed on it, so that their centres coincide. If both the rings are rotating about the same axis, then loss in kinetic energy is
View SolutionA charge q is spread uniformly over an isolated ring of radius 'R'. The ring is rotated about its natural axis and has magnetic dipole moment of the ring as M. Angular velocity of rotation is
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA thin circular ring of mass M and radius R is rotating about an axis perpendicular to the plane of the ring and passing through the centre with an angular velocity omega . Two bodies each of mass m are placed gently on the ring. The angular velocity with which the ring is rotating now is given by
View Solution
