A cavity pf radius r is present inside a solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a . An electron e is kept inside the cavity at an angle θ=45∘ as shown . how long will it take to touch the sphere again ?
 .Solution in Gujrati
.Solution in Gujrati
The correct Answer is:√6√2mr∈0eρa
The direction of electric field inside the cavity in -ve x direction and of constant magnitude ρa3∈0
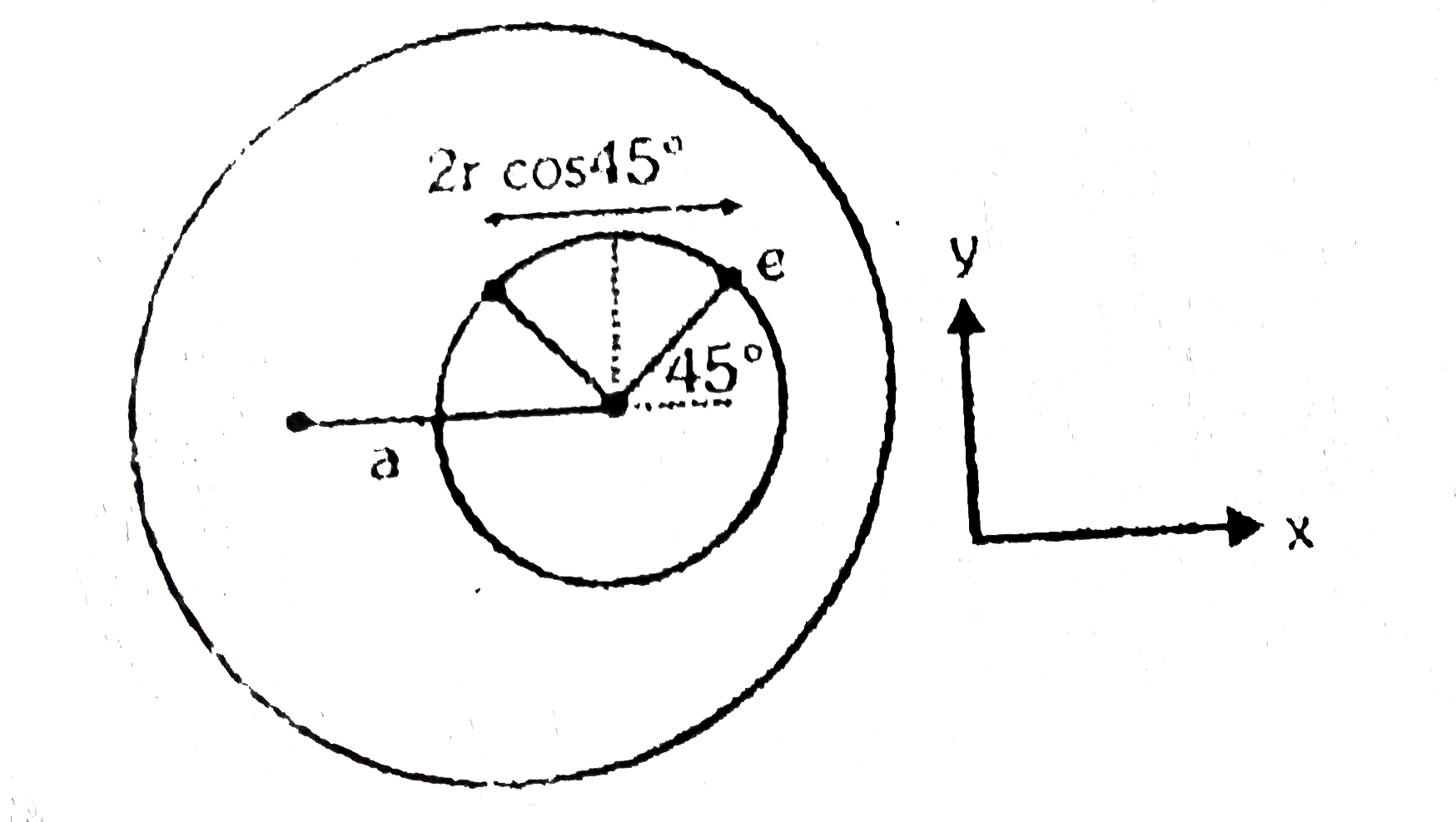
For touch the sphere again, electron must move 2rcos45∘ (as shown) distance
∴12[ρa3∈0×em]×t2=√2r∴t=√6√2mr∈0eρa
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)
35 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[A]
34 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
On moving a charge of 20 coulomb by 2cm, 2J of work is done , the potential difference between the points is .
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionThree particles, each of mass m and carrying a charge q each, are suspended from a common point by insulating mass-less strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is rho . An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View SolutionA cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of rho . The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle theta = 450 as shown. The electron (of mass m and charge –e) will take ((Psqrt(2)mrepsilon_(0))/(earho))^(1//2) time to touc the sphere again. Neglect gravity. find the value of P:
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is p. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and centre of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
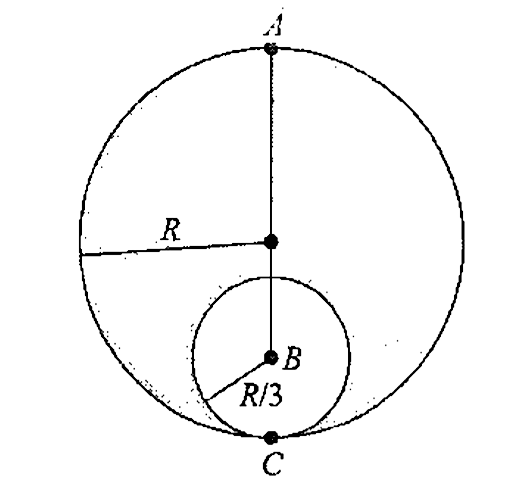
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA cavity of radius r is present inside a solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron e is kept inside the cavity at an angle θ=45∘ as shown. the electron (mass m and -e) touches the sphere again after time (P√2mrε0eaρ)1/2 ? Find the value of P. Neglect gravity.

View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View Solution7.Consider a uniform charged sphere of charge density p and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure.If the electric field at the centre of the cavity is (rho R)/(n varepsilon_(0)) find n .
View SolutionConsider a uniform charged sphere of charge density r and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure. If the electric field at the centre of the cavity is ρRnɛ0find n .
View SolutionA non conducting sphere of radius a is charged uniform with volume charge density rho . There is a spherical cavity in the sphere with radius b. The position vector of centre of the cavity with respect to centre of the original sphere is vecC . Find the electric field at any point inside the cavity whose position vector is vecr with respect to centre of the original sphere.
View Solution
