Figure shown a section through two long thin concentric cylinders of radii a & b with a>b. The cylinders have equal and opposite per unit length λ. Find the electric field at a distance r from the axis for (i) r<a (ii) a<r<b (iii) r>b
 Solution in Gujrati
Solution in Gujrati
[i] r<a⇒ Point inside ⇒E=0
[ii] a<r<b⇒ Point outside the inner and inside the outer so field due to only inner cylinder
hence E=2×λr
[iii] r>b⇒ point outside from both cylinders so the charge per unit length (λ) is zero point (r>b)∴E=0
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(A)
35 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[A]
34 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
On moving a charge of 20 coulomb by 2cm, 2J of work is done , the potential difference between the points is .
View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View SolutionThree particles, each of mass m and carrying a charge q each, are suspended from a common point by insulating mass-less strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionThree concentric spherical conductors of radii a, 2a, and 3a have charges -Q, +2Q , and -4Q , respectively. If r is the distance of the point under consideration from the center of the spheres, then find the electric field and potential due to the given configuration, for the values (i) r lt a (ii) a lt r lt 2a (iii) 2 a lt r lt 3 a r gt 3 a . .
View SolutionA thin spherical conducting shell of radius r_(1) carries a charge Q . Concentric with it is another thin metallic spherical shell of radius r_(2) (r_(2) gt r_(1)) . Calculate electric field at distance r when (i) r lt r_(1) ,(ii) r_(1) lt r lt r_(2) and (iii) r gt r_(2) . What will be the field in above cases if outer shell (a) is given charge q and (b) is earthed ?
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
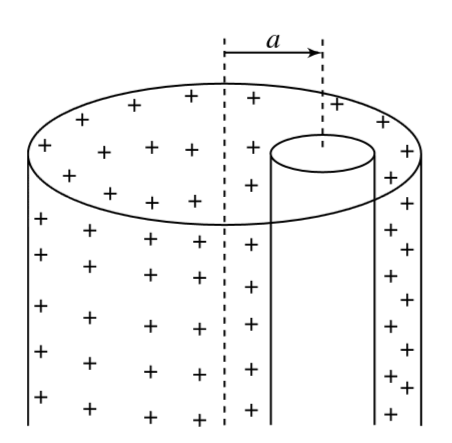
View SolutionA long straight cylindrical region of radius a curries a current along its length. The current density (J) varies from the axis to the edge of the cylindrical region according to J = J_(0) ( 1 – r / a) Where r is distance from the axis (0 lt r lta) (a) Find the mean current density. (b) Plot the variation of magnetic field (B) with distance r from the axis of the cylinder for 0 lt r lt a .
View SolutionThere are two co-axial non conducting cylinders of radii a and b(>a). Length of each cylinder is L(>>b) and their curved surfaces have uniform surface charge densities of–σ (on cylinder of radius a) and +σ (on cylinder of radius b). The two cylinders are made to rotate with same angular velocity ω as shown in the figure. The charge distribution does not change due to rotation. Find the electric field (E) and magnetic field (B) at a point (P) which is at a distance r from the axis such that (a) 0<r<a (b) a<r<b (c) r>b. Assume that point P is close to perpendicular bisector of the length of the cylinders

View SolutionWrite increasing order of basic strength of following: (i). (a) F^(ɵ) , (b). Cl^(ɵ) , (c). Br^(ɵ) , (d). I^(ɵ) (A). a gt b gt c gt d (B). d lt a lt c lt b (C). d gt a gt b gt c (D). a gt d gt c gt b (ii). (a). CH_(3)^(ɵ) , (b). Cl^(ɵ) , (c) OH^(ɵ) , (d). F^(ɵ) (A). a gt b gt c gt d (B). d lt a lt c lt b (C). d gt a gt b gt c (D). a gt d gt c gt b (iii). (a). R-NH_(2) , (b). Ph-NH_(2) , (c). R-underset(O)underset(||)(C)-NH_(2) (A). a gt b gt c (B). a lt c lt b (C). a lt b lt c (D). a gt c gt b (iv). (a). NH_(3) , (b). MeNH_(2) , (c). Me_(2)NH , (d). Me_(2)N (A). a lt b lt c lt d (B). d lt a lt c lt b (C). d gt a gt b gt c (D). a gt d gt c gt b
View SolutionA coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) r gt a , (b) a lt r lt b and (c) b gt r gt c
View SolutionIf a>b, then ac<bc for all a, b and c∈R, where c<0. (True /False)
View SolutionIf A={x:x∈R,x<5}andB={x:x∈R,x>4}, find A∩B.
View SolutionConsider a system of two long coaxial cylinders: solid (of radius a carrying i current in positive z direction) and hollow (or radius b carrying current i in negative z direction). Find the magnetic field at a point distant r from of the cylinders for
(i) r≤a
(ii) a<r<b
(iii) r>b

View SolutionThe electric field at a distance r from a long wire having charge per unit length λ is
View Solution
