According to Maxwell−distribution law, the probability function representing the ratio of molecules at a particular velocity to the total number of molecules is given by
f(v)=k1√(m2πKT2)34πv2e−mv22KT
Where m is the mass of the molecule, v is the velocity of the molecule, T is the temperature k and k1 are constant. The dimensional formulae of k1 is Solution in Gujrati
(a) L2T−2
(b) L1T−1K−3/2
(c) L1T−1K+3/2
(d) L2T−1K+3/2
The correct Answer is:C
Here f(v) is dimensionless and [mv2]=[kt]
[ki]=[(2πkT2m)1.514πv2]=[vT1.5]=[L1T−1K1.5]
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionDetermine the gas temperature at which
(a) the root mean square velocity of hydrogen molecules exceeds their most probable velocity by Δv=400m/s ,
(b) the velocity distribution function F(v) for the oxygen molecules will have the maximum value at the velocity v=420m/s.
View SolutionMaking use of the Maxwell distribution function, calculate the number v of gas molecules reaching a unit area of a wall per unit time, if the concentration of molecules is equal to n, the temperature to T, and the mass of each molecule is m.
View SolutionThe velocity distribution of molecules in a beam coming out of a hole in a vessel is described by the function F(v) = A v^3 e^(- mv^2//2 k T) , where T is the temperature of the gas in the vessel. Find the most probable values of (a) the velocity of the molecules in the beam , compare the result obtained with the most probable velocity of the molecules in the vessel , (b) the kinetic energy of the molecules in the beam.
View SolutionThe Maxwell-Boltzmann distribution of molecular speeds in a sample of an ideal gas can be expressed as
f=4√π(m2kT)3/2v2e−mv22kT.dv
Where f represent the fraction of total molecules that have speeds between v and v + dv.m, k and T are mass of each molecule, Boltzmann constant and temperature of the gas.
(a) What will be value of ∫v=∞v=0fdv?
(b) It is given that ∫∞0v3e−av2dv=12a2
Find the average speed of gas molecules at temperature T.
View SolutionAn HCl molecule has rotational, translational and vibrational motions. If the rms velocity of HCl molecules in its gaseous phase is vec(v), m is its mass and k_(s) is Bolzmann constant, then its temperature will be (mv^(2))/(nk_(B)) , where n is __________ .
View SolutionRead the following paragraph and answer the questions given below:
According to Maxwell distribution, the area under the curve is equal to the total number of molecules in collision. On increasing temperature, fraction of molecules having speed equal to ump (most probable speed) decreases. The speed distribution also depends on the mass of the molecules along with the temperature.
In general, the distribution depends upon the value of MT (where M is molar mass and T is temperature in kelvin).
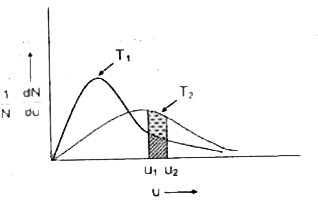
Choose the correct option:
Relationship between T1andT2 a is given as
View SolutionIf a unimolecular reaction, A(g) to Products, takes place according to the mechanism (I) A+Aoverset(k_(1))underset(k_(-1))(hArr)A^(a)+A (II) A^(a)underset(k_(2))(to)P where k_(1) , k_(-1) and k_(2) are the rate constants and P, A and A^(a) stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively. Which of the following expressions are correct?
View SolutionIf a unimolecular reaction, A(g) to Products, takes place according to the mechanism (I) A+Aoverset(k_(1))underset(k_(-1))(hArr)A^(a)+A (II) A^(a)underset(k_(2))(to)P where k_(1) , k_(-1) and k_(2) are the rate constants and P, A and A^(a) stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively. For the reaction scheme, X+Yoverset(k_(f))underset(k_(b))(hArr)Z , Y+Zoverset(k)(to)T , the rate equation for the formation of T will be
View SolutionIf a unimolecular reaction, A(g)→ Products, takes place according to the mechanism
(I)A+Ak1⇐===⇒k−1Aa+A
(II)Aa−−→k2P
where k1, k−1 and k2 are the rate constants and P,A and Aa stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively.
The order 'n' initial concentration a0 and time of half reaction t1/2, for a reaction are related as
View SolutionThe total energy of molecules is divided equally amongst the various degrees of freedom of a molecule. The distribution of kinetic energy along x, y, z axis are EKx,EKy,EKz
Total K.e =EKx+EKy+EKz
Since the motion of molecule is equally probable in all the three directions, therefore
EKx=EKy=EKz=13EK=13×32kT=12kT, where k=RNA = Botzman constant.
K.E.=12kT per molecule or =12RT per mole.
In vibration motion, molecules possess both kinetic energy as well as potential energy. This means energy of vibration involves two degrees of fiuedom.
Vibration energy =2×12kT=2×12RT [∴ two degrees of freedom per mole]
If the gas molecules have n1 translational degrees of freedom, n2 rotational degrees of freedom and n3 vibrational degrees of freedom, that total energy = n1[kT2]+n2[kT2]+n3[kT2]×2

Where 'n' is atomicity of gas.
The vibrational kinetic energy of CO2 molecule is
View SolutionThe total energy of molecules is divided equally amongst the various degrees of freedom of a molecule. The distribution of kinetic energy along x, y, z axis are E_(K_(x)), E_(K_(y)), E_(K_(z)) Total K.e =E_(K_(x)) + E_(K_(y)) + E_(K_(z)) Since the motion of molecule is equally probable in all the three directions, therefore E_(K_(x)) = E_(K_(y)) = E_(K_(z)) =1/3 E_(K) =1/3 xx 3/2 kT = 1/2 kT , where k =R/N_(A) = Botzman constant. K.E. = 1/2 kT per molecule or =1/2 RT per mole. In vibration motion, molecules possess both kinetic energy as well as potential energy. This means energy of vibration involves two degrees of fiuedom. Vibration energy =2 xx 1/2kT =2 xx 1/2RT [ therefore two degrees of freedom per mole] If the gas molecules have n_(1) translational degrees of freedom, n_2 rotational degrees of freedom and n_(3) vibrational degrees of freedom, that total energy = n_(1)[(kT)/2] + n_(2) [(kT)/2] + n_(3) [(kT)/2] xx 2 Where 'n' is atomicity of gas. The rotational kinetic energy of H20 molecule is equal to
View SolutionThe most probable velocity of the molecules is given by (m is mass of a molecule)
View Solution
