A bead is arranged to move with constant speed around a loop that lies in a vetical plane. The magnitude of the net force on the bead is Solution in Gujrati
maximum at the bottom
maximum at the top
maximum at the side points
the same at all points
The correct Answer is:A
Step by step video & image solution for A bead is arranged to move with constant speed around a loop that lies in a vetical plane. The magnitude of the net force on the bead is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionA bead slide freely along a curved wire lying on a horizontal surface at constant speed as shown in Fig
a. Draw the vectors repesenting the force exerted by the wire on the bead at point A ,B and C
b. Suppose the bead in figure speeds up with constant tangential acceleration as it moves toward the right Draw the vector representing the force on the bead at point A B and C

View SolutionA head slide without friction around a loop the (figure). The bead slide is released is from rest at a height h = 3.50R . How large is the normal force on the bead at point (A) if its mass is 50 g ?
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
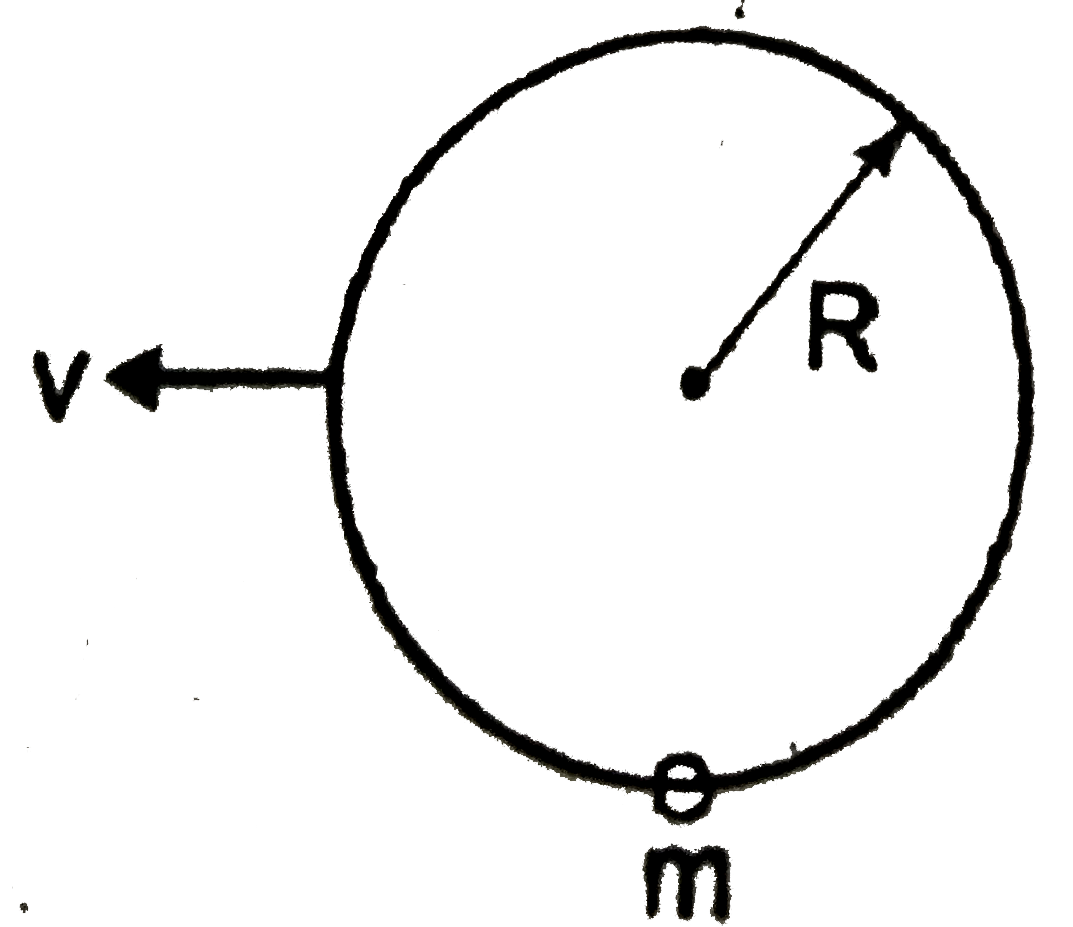
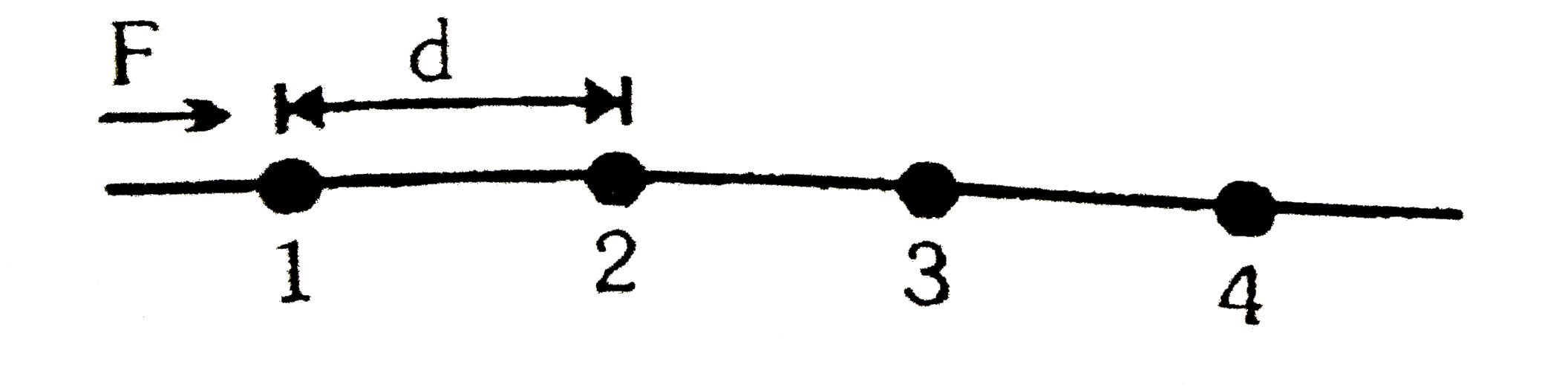
View SolutionThe Fig. showns a string of equally placed beads of mass m, separated by distance. The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic,
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v_(0) prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then
View SolutionA bead is moving on a frictionless fixed circular wire of radius 0.8 m in horizontal plane with constant speed & there is no interaction force between bead & wire & it is also connected with string & spring .
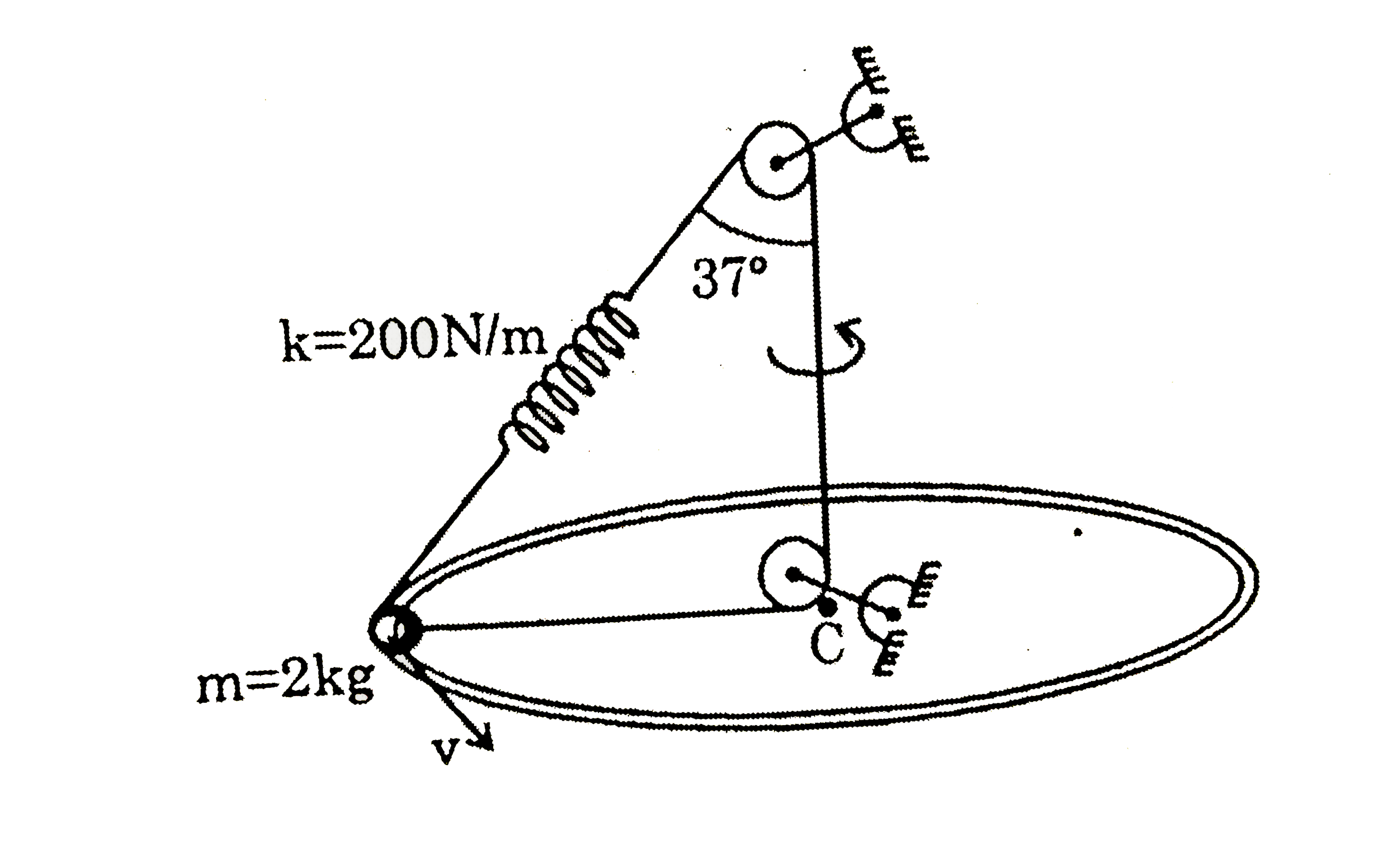
View SolutionA circular loop has a small bead which can slide on it without friction. The radius of the loop is r. Keeping the loop vertically it is rotated about a vertical diameter at a constant angular speed omega . What is the value of angle theta , when the bead is in dynamic equilibrium ?
View SolutionThe ratio of red beads to green beads is 2 : 3
How many green beads are needed to go with 12 red beads ?
View SolutionA bead slide freely along a curved wire lying on a horizontal surface at constant speed as shown in Fig
a. Draw the vectors repesenting the force exerted by the wire on the bead at point A ,B and C
b. Suppose the bead in figure speeds up with constant tangential acceleration as it moves toward the right Draw the vector representing the force on the bead at point A B and C

View SolutionThe ratio of red beads to green beads is 2 : 3
How many green beads are needed to go with 12 red beads ?
View SolutionDo you observe any pattern in arrangement of bead?
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
View Solution
