A ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
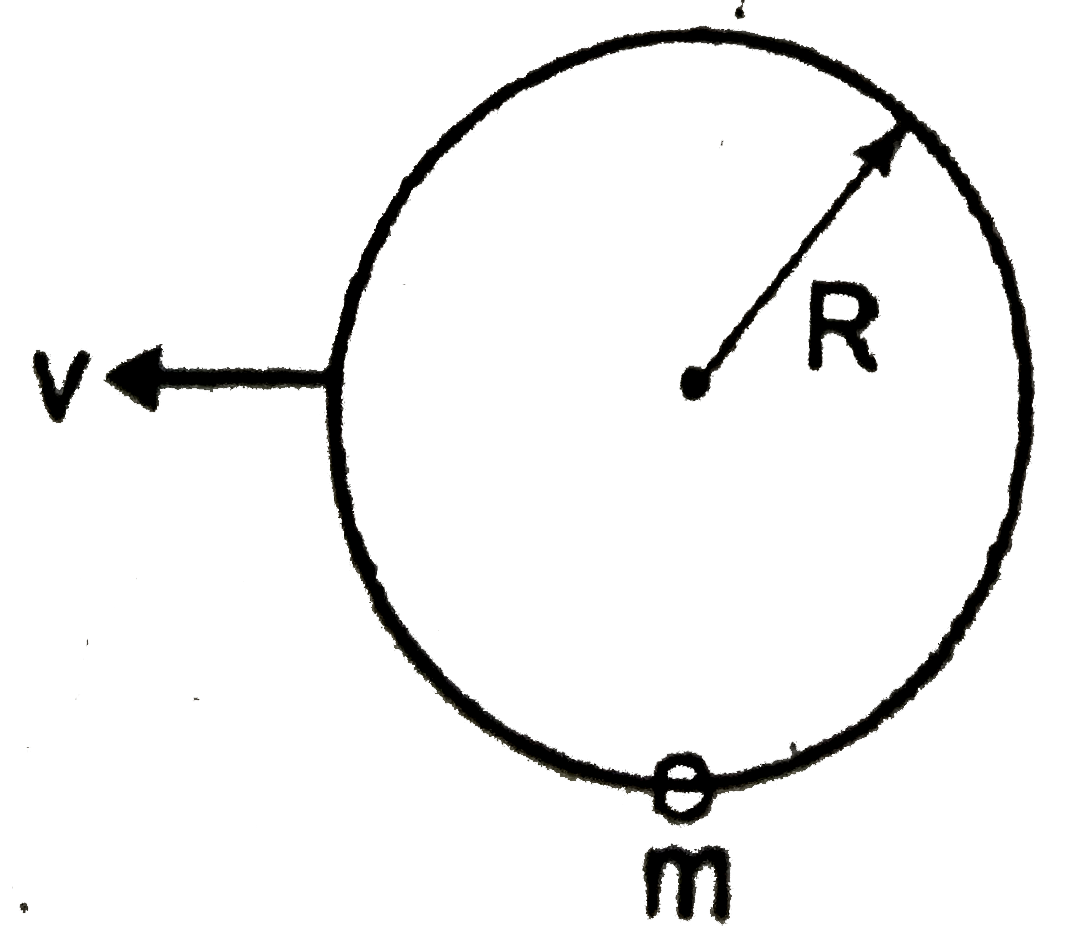
√3gR
√4gR
√5gR
√5.5gR
The correct Answer is:B
In the frame of ring ( inertial w.r.t. earth ), the initial velocity of the bead is v at the lowest position.

The condition for bead to complete the vertical circle is, its speed at top position.
vtop≥0
From conservation of energy
12mv2top+mg(2R)=12mv2
or v=√4gR
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 50
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 51
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 48
4 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
View SolutionA ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if m>3M2
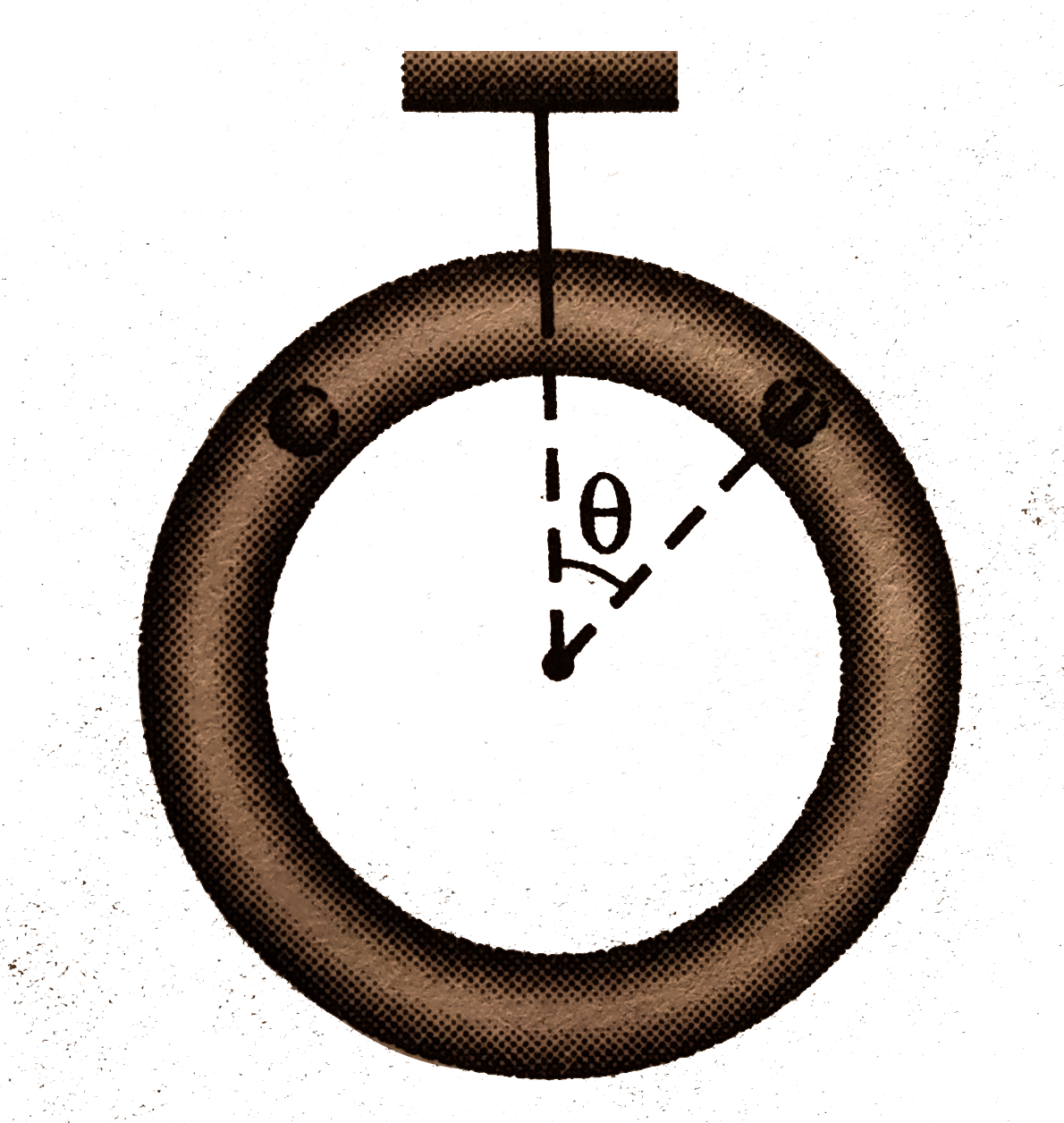
View Solution
Knowledge Check
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
Aa/gkBa/2gkC2a/gkDa/4gk

The figure shows a thin ring of mass M=1kg and radius R=0.4m spinning about a vertical diameter (take I=12MR2) A small beam of mass m=0.2kg can slide without friction along the ring When the bead is at the top of the ring the angular velocity is 5rad/s What is the angular velocity when the bead slips halfwat to θ=45∘?
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
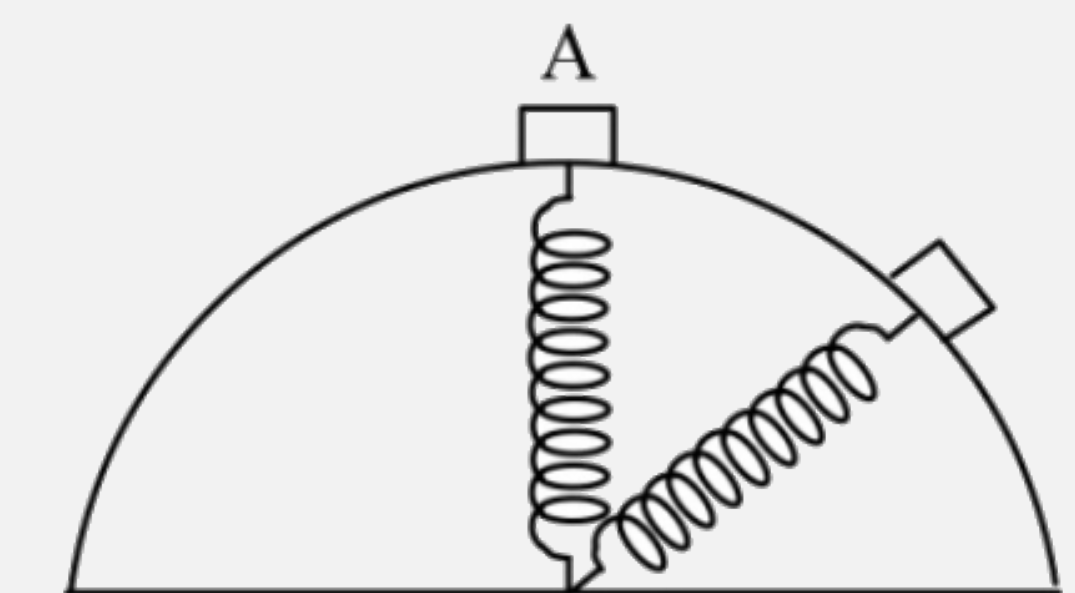
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View SolutionAn isolated smooth ring of mass M = 2m with two small beads each of mass m is as shown in the figure. Initially both the beads are at diametrically opposite points and have velocity v0 (for each) in same direction. The speed of the beads just before they collide for the first time is (complete system is placed on a smooth horizontal surface and assume each point of ring is touching the surface)

View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View Solution
