A particle is projected with a velocity of 30m/s at an angle 60∘ above the horizontal on a slope of inclination 30∘. Find its time of flight.Solution in Gujrati
The coordinate system, projection velocity and its component, and acceleration due to gravity and its component are shown in the adjoining figure. Subsituting corresponding values in following equation, we get the time of flight.
T=2uyay→T=2×155√3=2√3s
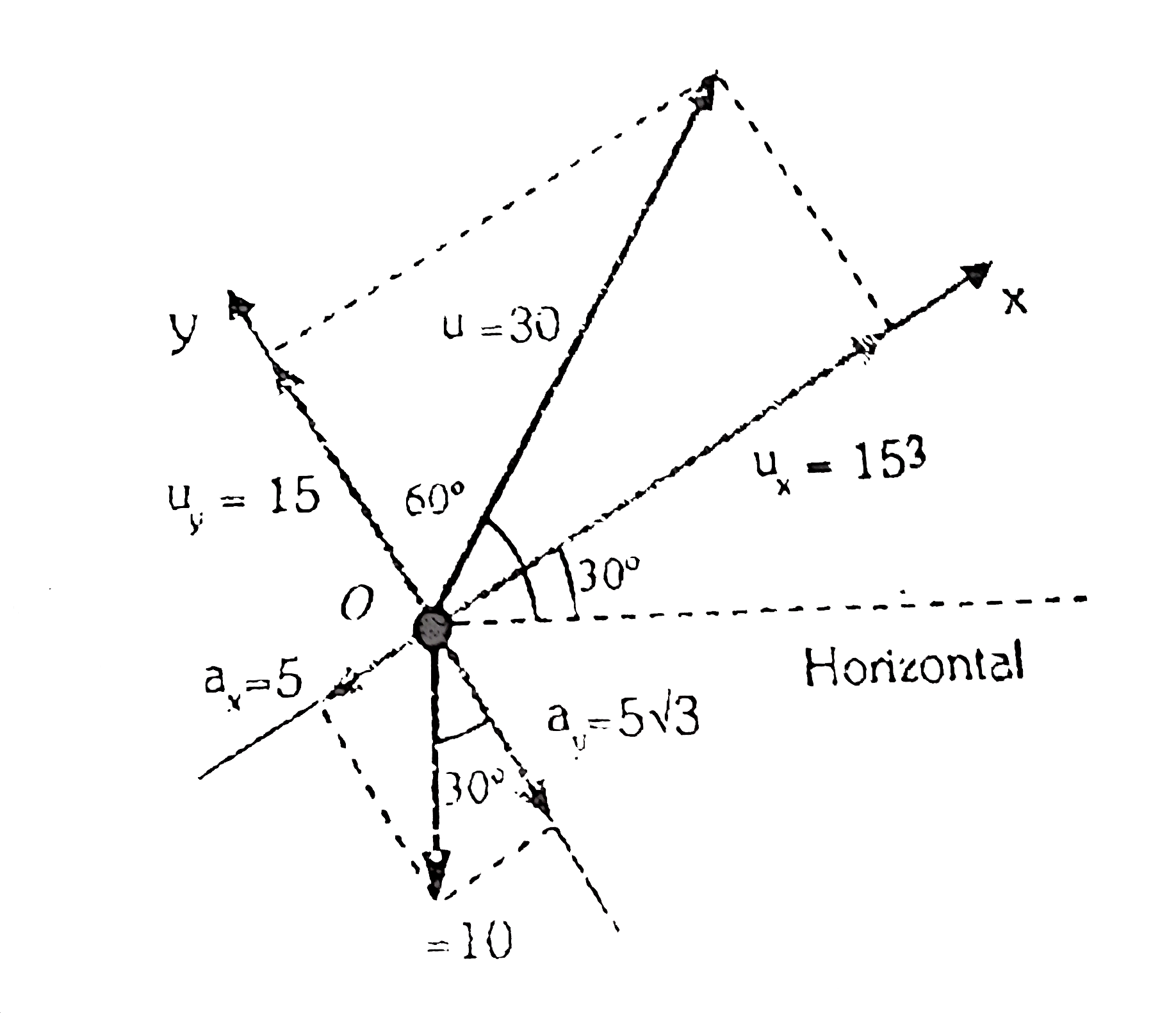
Substituting value of time of flight in following equation, we get the range R.
R=uxT−12axT2⇒R=15√3×2√3−12×5×(2√3)2=60m
In the adjoining figure, components of velocity →vP when the projectile hits the slope at point P are shown. The angle β which velocity vector makes with the x-axis is known as angle of hit. The projectile hits the slope with such a velocity →vP, whose y-component is equal in magnitude to that of velocity of projection. The x-component of velocity vx is calculated by substituting value of time of flight in following equation.
vx=ux−axt→vx=15√3−5×2√3=5√3
β=tan−1(vyvx)→β=60∘

Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-0155videos
KINEMATICS
- BOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-0257videos
KINEMATICS
- BOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
A bird moves from point (1,−2,3) to (4,2,3). If the speed of the bird id 10m/s, then the velocity of the bird is :-
06:22View SolutionA particle is moving in a plane with velocity given by →u=u0ˆi+(aωcosωt)ˆj, where ˆi and ˆj are unit vectors along x and y axes respectively. If particle is at the origin at t=0. Calculate the trajectory of the particle :-
02:22View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
02:31View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
02:18View SolutionA particle is projected with a velocity of 30 m//s at an angle 60^(@) above the horizontal on a slope of inclination 30^(@) . Find its range, time of flight and angle of hit.
03:10View SolutionTwo particle are projected with same initial velocities at an angle 30^(@) and 60^(@) with the horizontal .Then
03:25View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60^(@) with the horizontal from a point on an incline plane, making an angle of 30^(@) with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
View SolutionA body is projected with a velocity of 30 ms^(-1) at an angle of 30^(@) with the vertical. Find the maximum height, time of flight and the horizontal range.
05:18View SolutionA particle is projected at an angle of 60∘ above the horizontal with a speed of 10m/s. After some time the direction of its velocity makes an angle of 30∘ above the horizontal. The speed of the particle at this instant is s
05:06View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30^(@) to an inclined plane of inclination 30^(@) to the horizontal. The particle hits the inclined plane at an angle 30^(@) , during its journey. The time of flight is -
01:17View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30^@ with a plane of inclination 30^@ with respect to the horizontal . The particle hits the inclined plane at an angle of 30^@ . Find the (a) time of impact, (b) the height of the point of impact from the horizontal plane passing through the point of projection.
View SolutionA particle is projected from the surface of the earth with a speed of 20 m* s^(-1) at an angle 30^@ with the horizontal . The time of flight of that particle is
03:59View SolutionA particle is projected with a velocity of 25 m//s at an angle of 30^(@) with the horizontal . Calculate (i) The maximum height , (ii) time of flight and (iii) horizontal range .
03:09View SolutionA body is projected at angle 30° to horizontal with a velocity 50 msl. Its time of flight is (g=10m/s2)
01:50View SolutionA body is projected at angle 30^(@) to horizontal with a velocity 50ms^(-1) . Its time of flight is (g=10m//s^(2))
03:09View Solution

