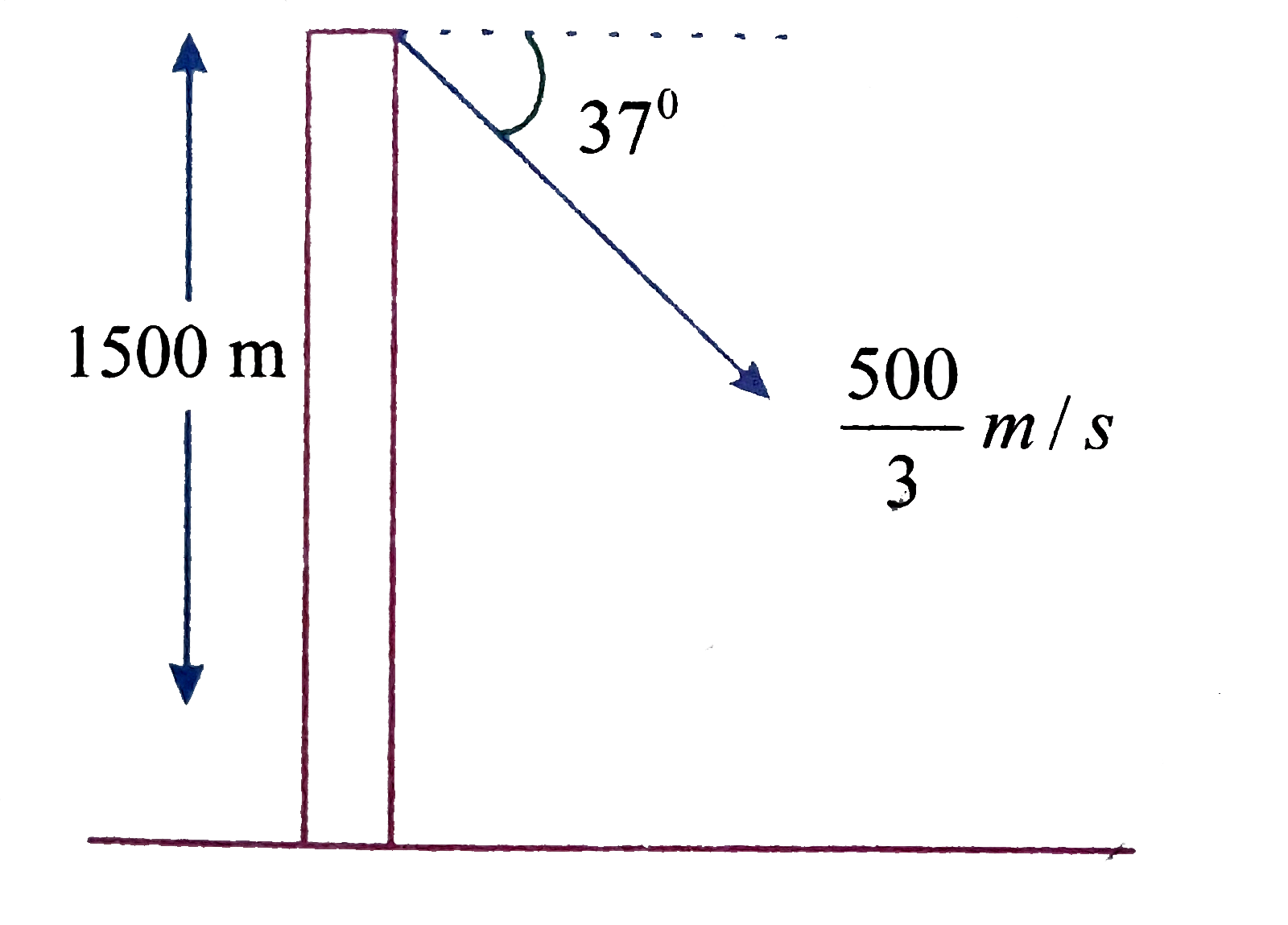
A particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:A
Distance (Horizontal)
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-03
6 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A particle is moving in a plane with velocity given by →u=u0ˆi+(aωcosωt)ˆj, where ˆi and ˆj are unit vectors along x and y axes respectively. If particle is at the origin at t=0. Calculate the trajectory of the particle :-
View SolutionThe equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionIn the figures shown, three particles are thrown from a tower of height 40 m as shown in figure. In each case find the time when the particles strike the ground and the distance of this point from foot of the tower. , , .
View SolutionA particle is projected from a tower of height 25 m with velocity 20sqrt(2)m//s at 45^@ . Find the time when particle strikes with ground. The horizontal distance from the foot of tower where it strikes. Also find the velocity at the time of collision.
View Solutiona shot is fired at an angle of 30∘ with horizontal from the top of a tower 182.88 metres high. The velocity of projection is 560.96m/s. Find where from the foot of tower it strikes the ground.
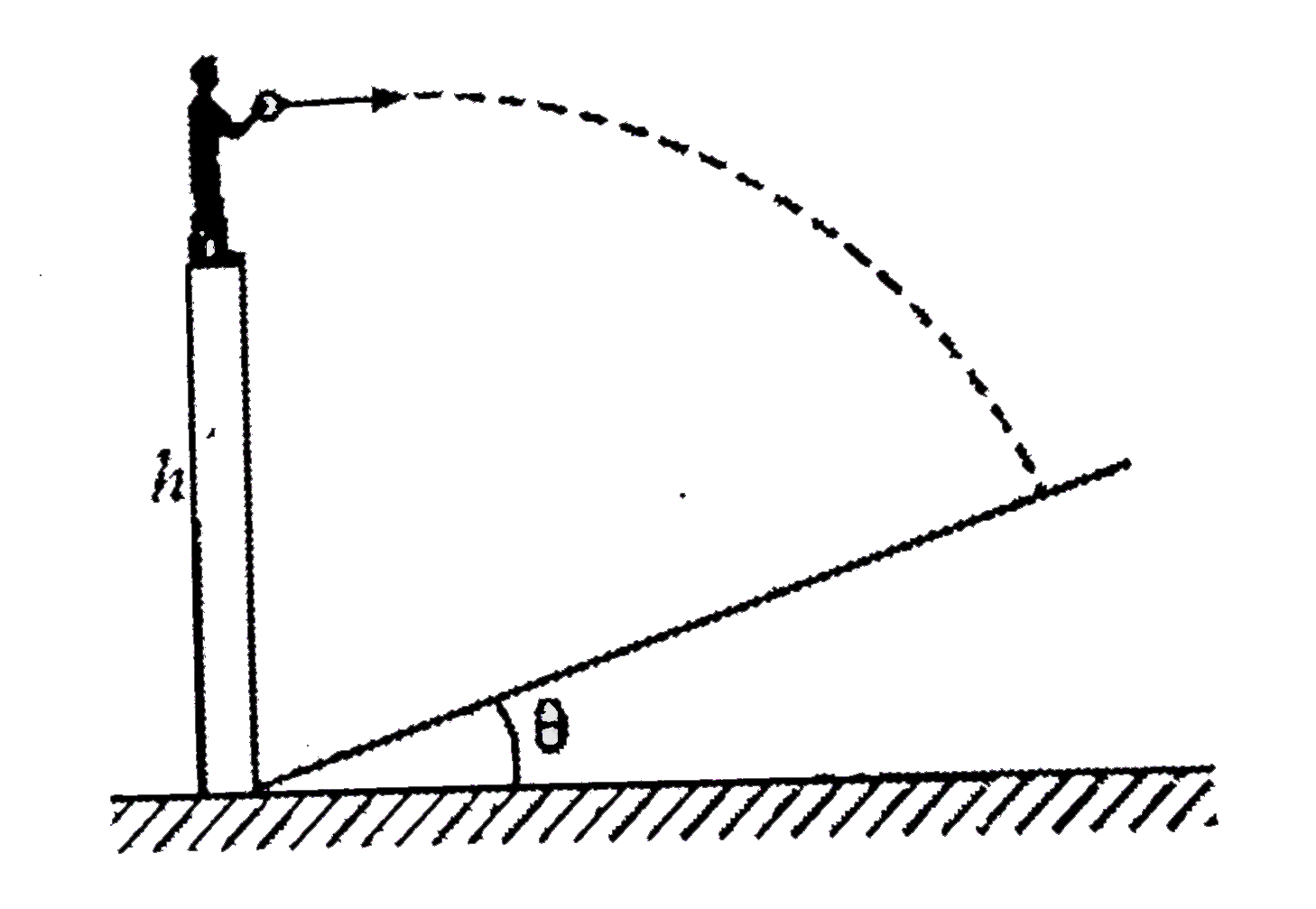
View SolutionA partacle is thrown in horizontal direction with speed u from a point P, the top of a tower shown in figure.1.49 at a vertical height h above the inclined plane of inclination θ. Find the speed with which the particle is thrown so that it strikes the plane normally. Also find the distance from the foot of the tower where the particle will strike.
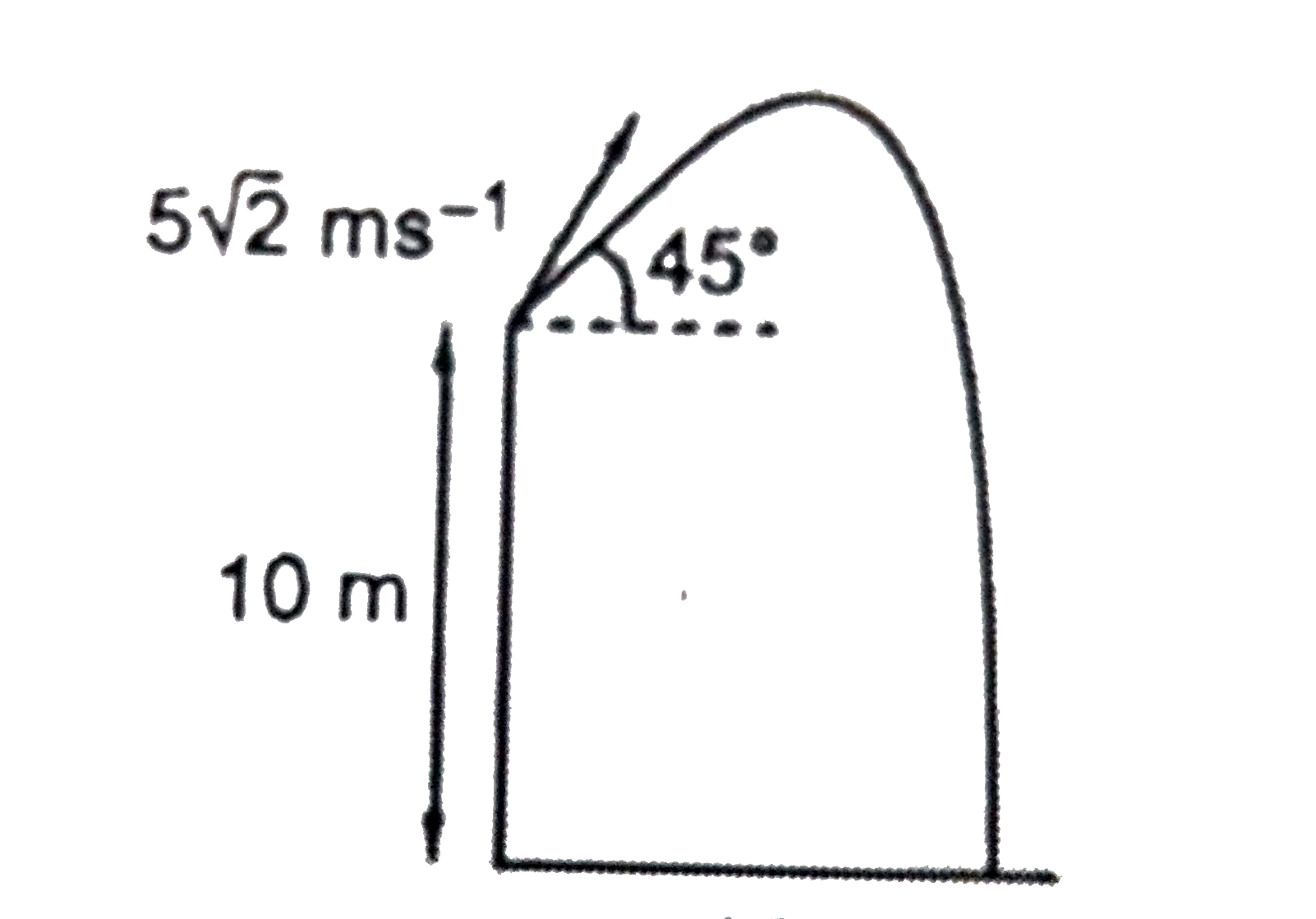
View SolutionParticle projected from tower fo heigh 10m as shown in figure. Find the time (in sec) after which particle will hit the ground.
View SolutionA stone is projected at an angle alpha to the horizontal from the top of a tower of height 3h If the stone reaches a maximum height h above the tower, then calculate the distance from the foot of the tower where particle strikes the foot of the where particle strikes the ground.
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionA particle is thrown horizontally from a tower of height 20m . If the speed of projection is 20m/s then the distance of point from the tower,where the particle hit the ground is:-
View SolutionA body thrown horizontally from the top of a tower touches the ground at a distance of 160m from the foot of the tower.If the velocity of projection is 40m/s then the height of the tower is (g=9.8ms2)
View SolutionThere is a tower of height 20m and a particle is projected up from top of the tower with an initial speed 20m//s. Top of the tower is marked as point A, from where particle is projected. Point of maximum height a denoted as B. When particle reaches the point A during downward journey then we call the same point as C. Point at the bottom of tower is marked as D where particle finally strikes. Acceleration due to gravity g=10m/s2
Time taken by the particle to reach the ground is
View Solution
