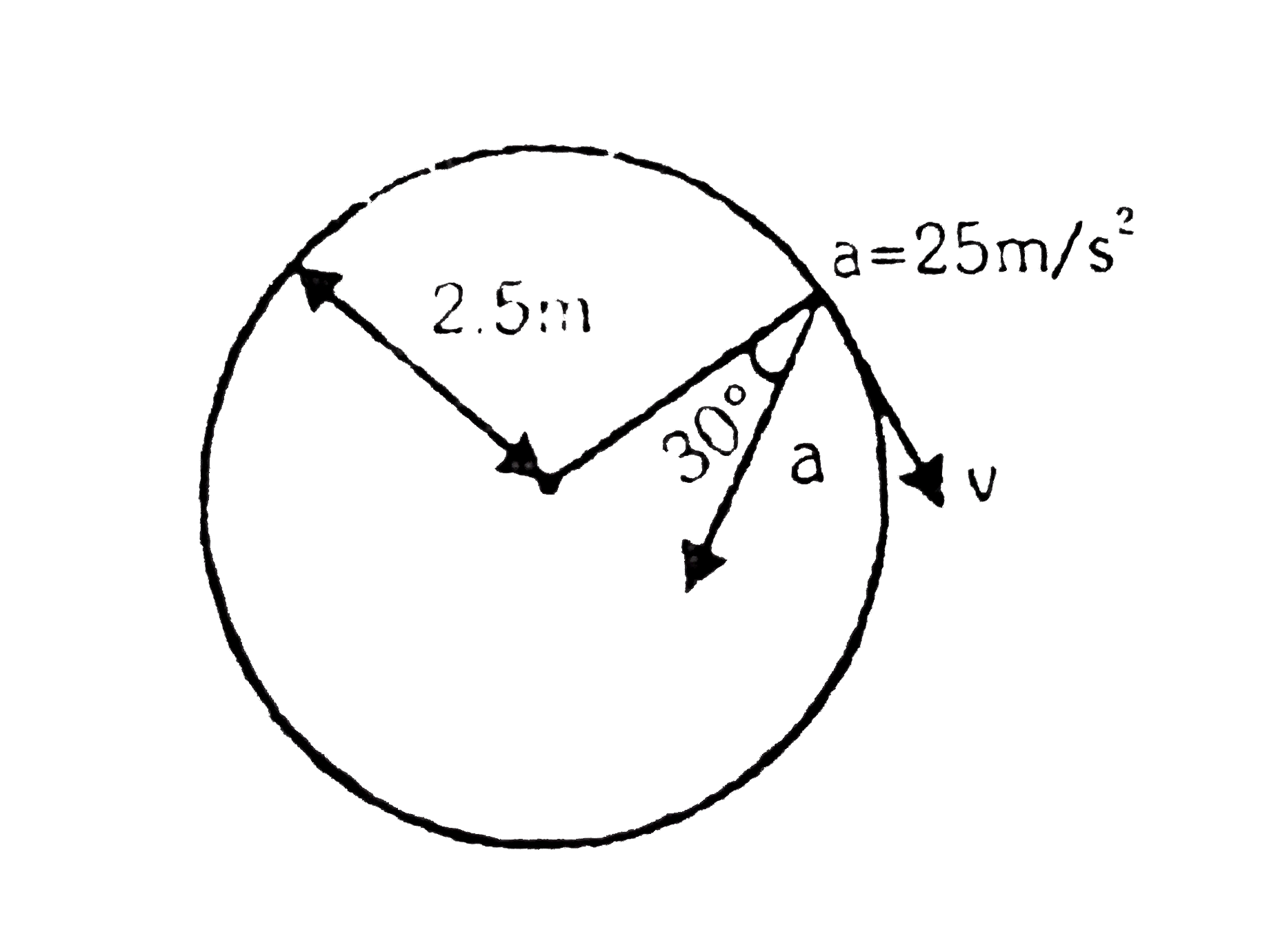
Figure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:(i) 25√32m/s2 (ii) (125√34)1/2m/s (iii) 252m/s2
r=2.5m,anet=25m/s2
(a) Radial acceleration =25cosθ=25×√33m/s2
(b) 25√32=v225⇒v=(125√34)1/2m/s
(c) Tangential acceleration =25sinθ=25×12m/s2
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-04[B]
14 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05 [A]
11 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#7
3 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20kmh−1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
View SolutionA ball whose kinetic energy is E , is projected at an angle of 45∘ to the horizontal . The kinetic energy of the ball at the highest point of its flight will be
View SolutionA projectile is projected with some initial velocity and some initial angle of projection. A wind is also blowing, due to which constant horizontal retardation a is imparted to the particle in the plane of motion. It is found that, the particle is at same height at two different time t1 & t2 and particle is at same horizontal distance at two different time t3 & t4
Angle of projection of particle is :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionFigur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find: (a) the radius acceleration, (b) the speed of the acceleration, (c) its tangential acceleration.
View SolutionFigure shows the direction of the total acceleration and velocity of a particle moving clockwise in a circle radius m at an instant of time. Tangential acceleration this instant is 5m//s^(2) . Which of the following statements is not correct?
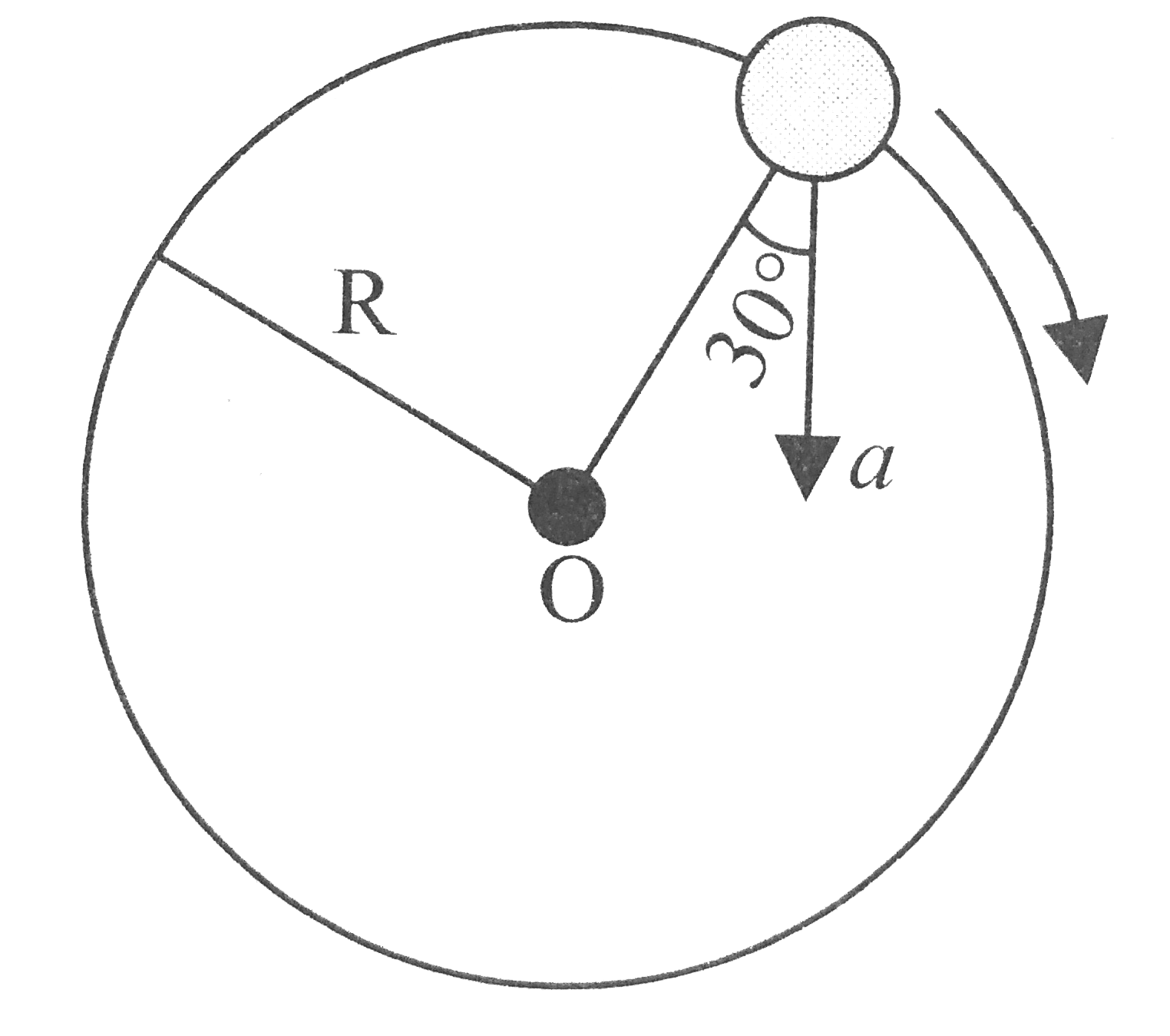
View SolutionIn the given figure, a=15m/s2 represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5m at a given instant of time. The speed of the particle is.
View SolutionA particle is moving in a circle of radius R and its speed is given by v=lambdat^(2) , where lambda is a constant. Find (a) radial acceleration, (b) tangential acceleration, ( c) resultant acceleration and (d) angle between acceleration and velocity.
View SolutionFigure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
View SolutionIn the given figure, a=15m//s^(2) represents the total acceleration of a particle moving in the clockwise dirction in a circle of radius R=2.5 m at a given instant of time. The speed of the particle is
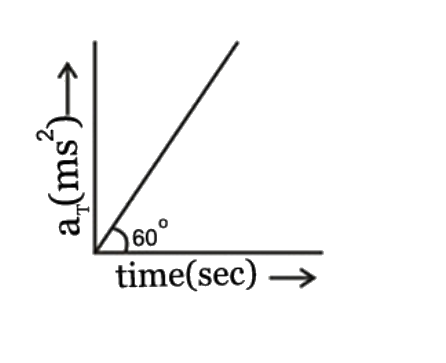
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
View SolutionThe figure shows the total acceleration a = 32 m s^(-2) of a moving particle moving clockwise in a circle of radius R = 1 m . What are the centripetal acceleration a and speed of the particle at the given instant ?
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View SolutionIn the given figure, a=15 m//s^2 represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5 m at a given instant of time. The speed of the particle is
View SolutionTangential acceleration of a particle moving on a circle of radius 1 m varies with time t as shown in the graph (initial velocity of particle is zer). Time after which total acceleration of particle makes an angle of 30^@ with radial acceleration is,
View Solution
