A projectile can have the same range 'R' for two angles of projection . If 'T1' and 'T2' to be times of flights in the two cases, then the product of the two times of flights is directly proportional to . Solution in Gujrati
R2
1R2
1R
R
The correct Answer is:4
When a body is projected at an angles θ and 90−θ, the ranges for both angles are equal and the corresponding time of flights for the two ranges are t1 and t2.
R=2u2sinθcosθg=12g(2usinθg)(2usin(90∘−θ)g)
=12gt1t2⇒R∝t1t2
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05[B]
5 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - MCQ with one or more than one correct Question
1 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-04[B]
14 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A particle goes from point A and B, moving in a semcircle of raidus 1.0m, in 1.0 s, as shown in the figure. The magnitude of the average velocity of the particle is
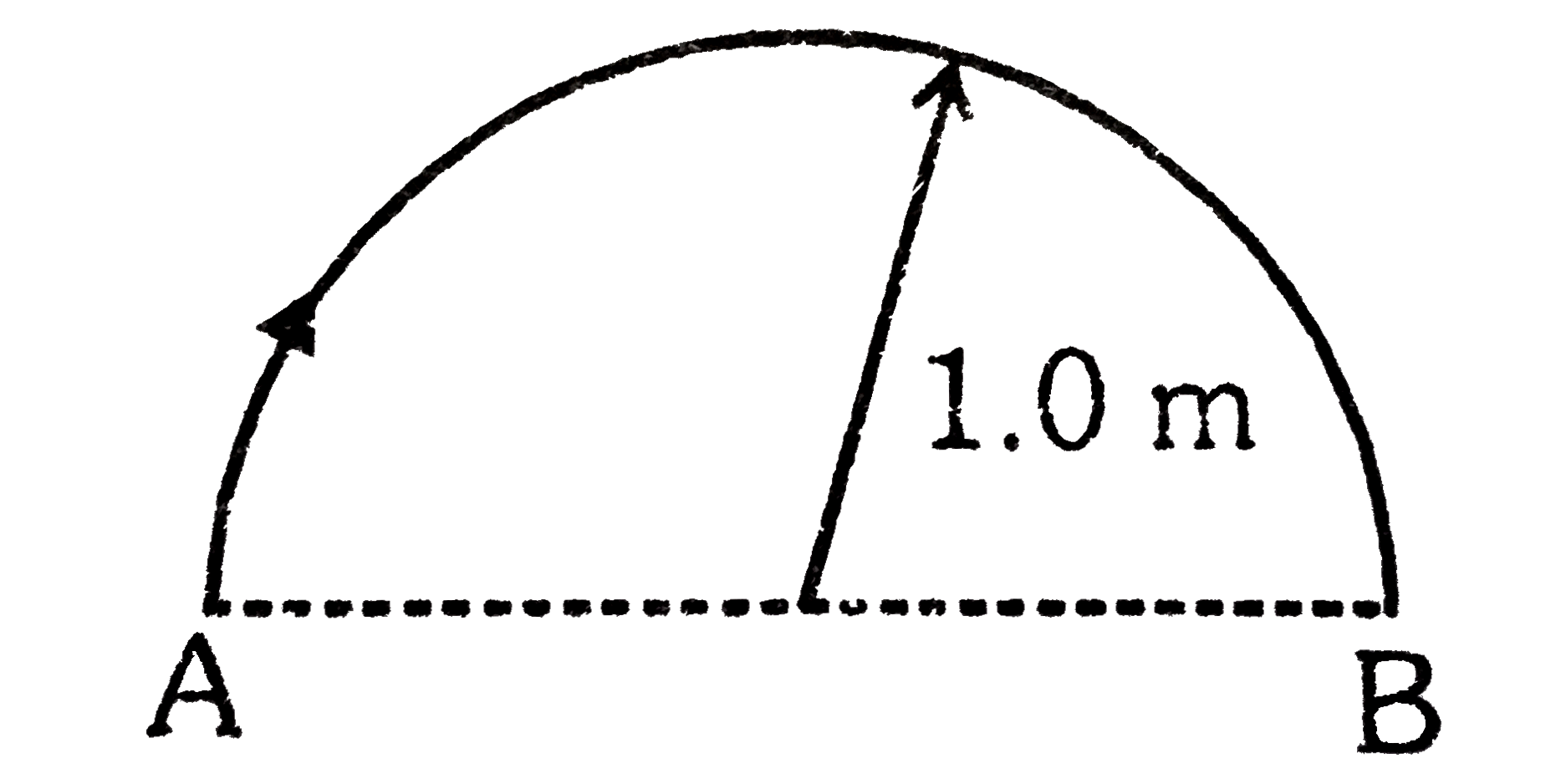
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionTwo towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20kmh−1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA projectile can have the same range 'R' for two angles of projection . If 'T1' and 'T2' to be times of flights in the two cases, then the product of the two times of flights is directly proportional to .
View SolutionA projectile can have same range R for two angles of projection. It t_1 and t_2 are the times of flight in the two cases, then what is the product of two times of flight ?
View SolutionA projectille can have the same rangeR for two angles of projection. If t1 and t_(2)bethetimeofflight∈thetwocases,thenf∈dtherelationbetween t_(1), t_(2)andR .
View SolutionFor a given velocity, a projectile has the same range R for two angles of rpojection if t_(1) and t_(2) are the times of flight in the two cases then
View SolutionA projectile has the same range R for two angles of projections but same speed. If T1 and T2 be the times of flight in the two cases, then
Here θ is the angle of projection corresponding to T1.
View SolutionA projectile can have the same range R for two angles of projection. If t_(1) and t_(2) be the times of flight in the two cases:-
View SolutionA projectile has same range for two angules of projection. If times of flight in two cases are t_(1) and t_(2) then the range of the projectilie is
View SolutionA projectile has same range R for the two angles of projection. If T_(1) and T_(2) are the times of flight in two cases, then:
View SolutionA projectile can have the same range 'R' for two angles of projection. If t1 and t2 be the times of flight in the two cases, then product of the two times of flights is proportional to :
View SolutionFor a given velocity, a projectile has the same range R for two angles of projection if t1andt2 are the time of flight in the two cases then
View SolutionA projectile can have the same range R for two angles of projection .If t1and t2be the times of flight in the two cases, then the product of the two times of fight is directly proportional to
View Solution
