A particle is moving with velocity →v=k(yˆi+xˆj), where k is a constant . The genergal equation for its path is Solution in Gujrati
y2=x2+ constant
y=x2+ constant
y2=x+ constant
xy= constant
The correct Answer is:1
→v=K(yˆi+xˆj),vx=ky,dxdt=ky
similarly dydt=Kx
Hence dydx=xy⇒ydy=xdx,
by integrating y2=x2+c
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05[B]
5 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - MCQ with one or more than one correct Question
1 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-04[B]
14 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A particle goes from point A and B, moving in a semcircle of raidus 1.0m, in 1.0 s, as shown in the figure. The magnitude of the average velocity of the particle is
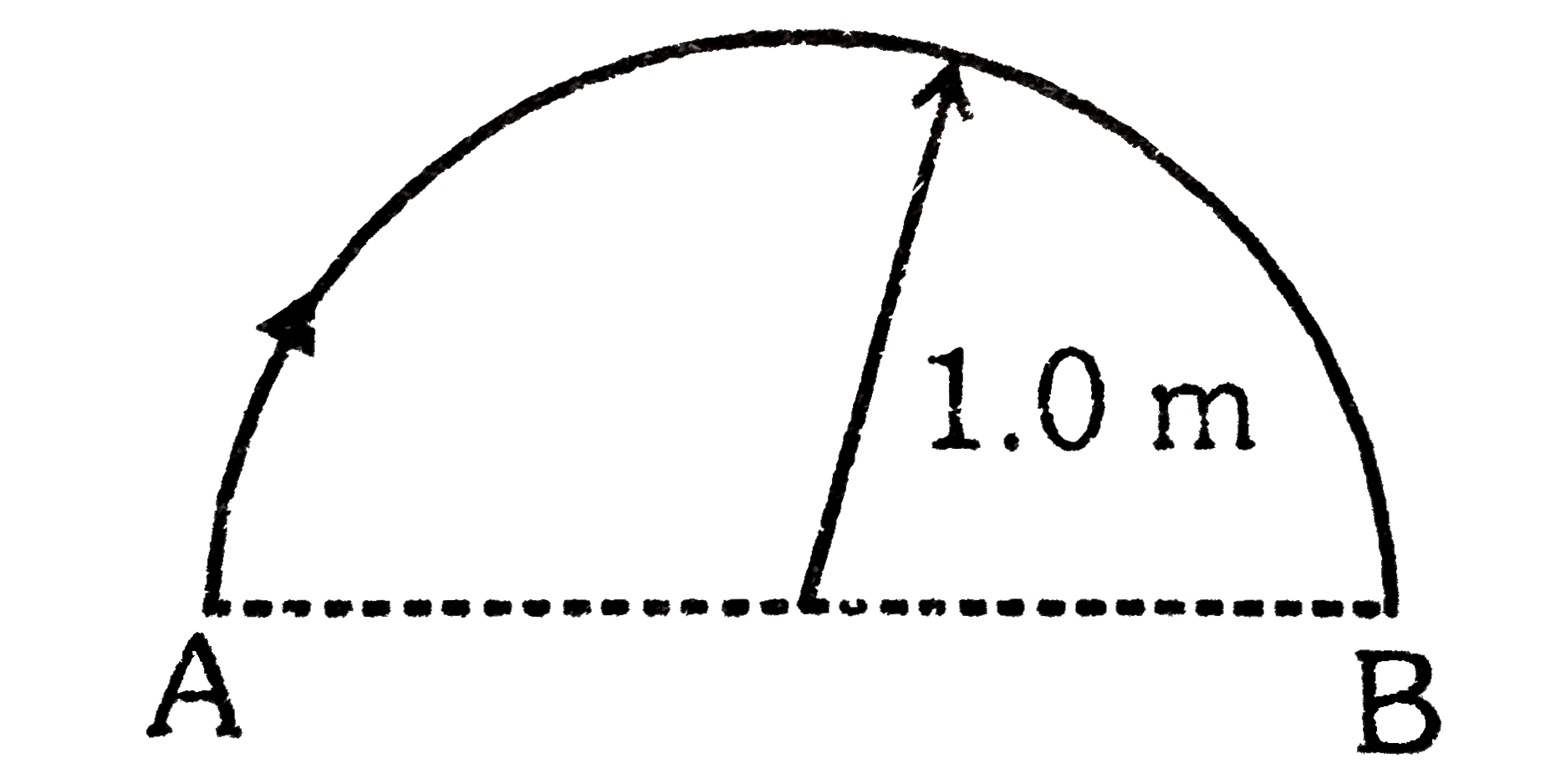
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionTwo towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20kmh−1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road ?
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA particle is moving with velocity vecv = k( y hat^(i) + x hat(j)) , where k is a constant . The genergal equation for its path is
View SolutionA particle is moving with speed 6m/s along the direction of →A=2ˆi+2ˆj−ˆk, then its velocity is :
View SolutionThe velocity of particle is 3ˆi+2ˆj+3ˆk. Find the vector component of the velocity along the line ˆi−ˆj+ˆk.
View Solutionयदि ˆi,ˆj,ˆk क्रमशः X,Y,Z अक्ष की दिशा में एकांक सदिश हो तो सिद्ध कीजिये -
(a) ˆi⋅ˆi=ˆj⋅ˆj=ˆk⋅ˆk=1
(b) ˆi⋅ˆj=ˆi⋅ˆk=ˆj⋅ˆk=0
(c) ˆi׈i=ˆj׈j=ˆk׈k=0
View Solutionएक कण का वेग →v=k(yˆi+xˆj)से गतिमान है , जहाँ एक स्थिरांक है | इसके पथ का व्यापक समीकरण है -
View SolutionA particle is moving with a velocity, →v=K(yˆi+xˆj), where K is a constant. The general equation for the path is:
View Solutionযদি (x,y,z)≠(0,0,0) এবং (ˆi+ˆj+3ˆk)x+(3ˆi−3ˆj+ˆk)y+(−4ˆi+5ˆj)z=a(xˆi+yˆj+zˆk) হয়, তবে a-এর মান হবে-
View SolutionFind the values of λ such that x,y,z≠(0,0,0) and (ˆi+ˆj+3ˆk)x+(3ˆi−3ˆj+ˆk)y+(−4ˆi+5ˆj)z=λ(xˆi+yˆj+zˆk), where ˆi,ˆj,ˆk are unit vector along coordinate axes.
View SolutionEvaluate : [ˆiˆjˆk]+[ˆjˆkˆi]+[ˆkˆiˆj] [2ˆiˆjˆk]+[ˆiˆkˆj]+[ˆkˆj2ˆi]
View SolutionEvaluate : [ˆiˆjˆk]+[ˆjˆkˆi]+[ˆkˆiˆj] [2ˆiˆjˆk]+[ˆiˆkˆj]+[ˆkˆj2ˆi]
View SolutionA particle is moving with velocity vecv = k( y hat(i) + x hat(j)) , where k is a constant . The genergal equation for its path is
View Solution
