The coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then Solution in Gujrati
The path of the particle is an ellipse
The velocity and acceleration of the particle are normal to each other at t=π/2p
The acceleration of the particle is always directed towards a focus.
The distance travelled by the particle in time interval t=0 to t=π2p is a
The correct Answer is:A, B, C
x=acospt,y=bsinpt,→r=acos(pt)ˆi+bsin(pt)ˆj
∵sin2pt+cos2pt=1
∴x2a2+y2b2=1 (ellipse)
→v=−apsin(pt)ˆi+bpcos(pt)ˆj,vt=π2p=−apˆi
→a=−ap2(pt)ˆi=bp2sin(pt)ˆj,at=π2p=−bp2ˆj
→a.→v=0
→a=−p2[acosptˆi+bsinptˆj]=−p2→r
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - SUBJECTIVE QUESTION
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05[B]
5 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A large heavy box is sliding without friction down a smooth plane of inclination θ. From a point P on the bottom of the box, a particle is projected inside the box. The initial speed of the particle with respect to box is u and the direction of projection makes an angle α with the bottom as shown in figure.

(i) Find the distance along the bottom of the box between the point of projection P and the point Q where the particle lands. (Assume that the particle does not hit any other surface of the box. Neglect air resistance).
(ii) If the horizontal displacement of the particle as seen by an observer on the ground is zero, find the speed of the box with respect to the ground at the instant when the particle was projected.
View SolutionA train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60(∘) to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View SolutionA particle goes from point A and B, moving in a semcircle of raidus 1.0m, in 1.0 s, as shown in the figure. The magnitude of the average velocity of the particle is
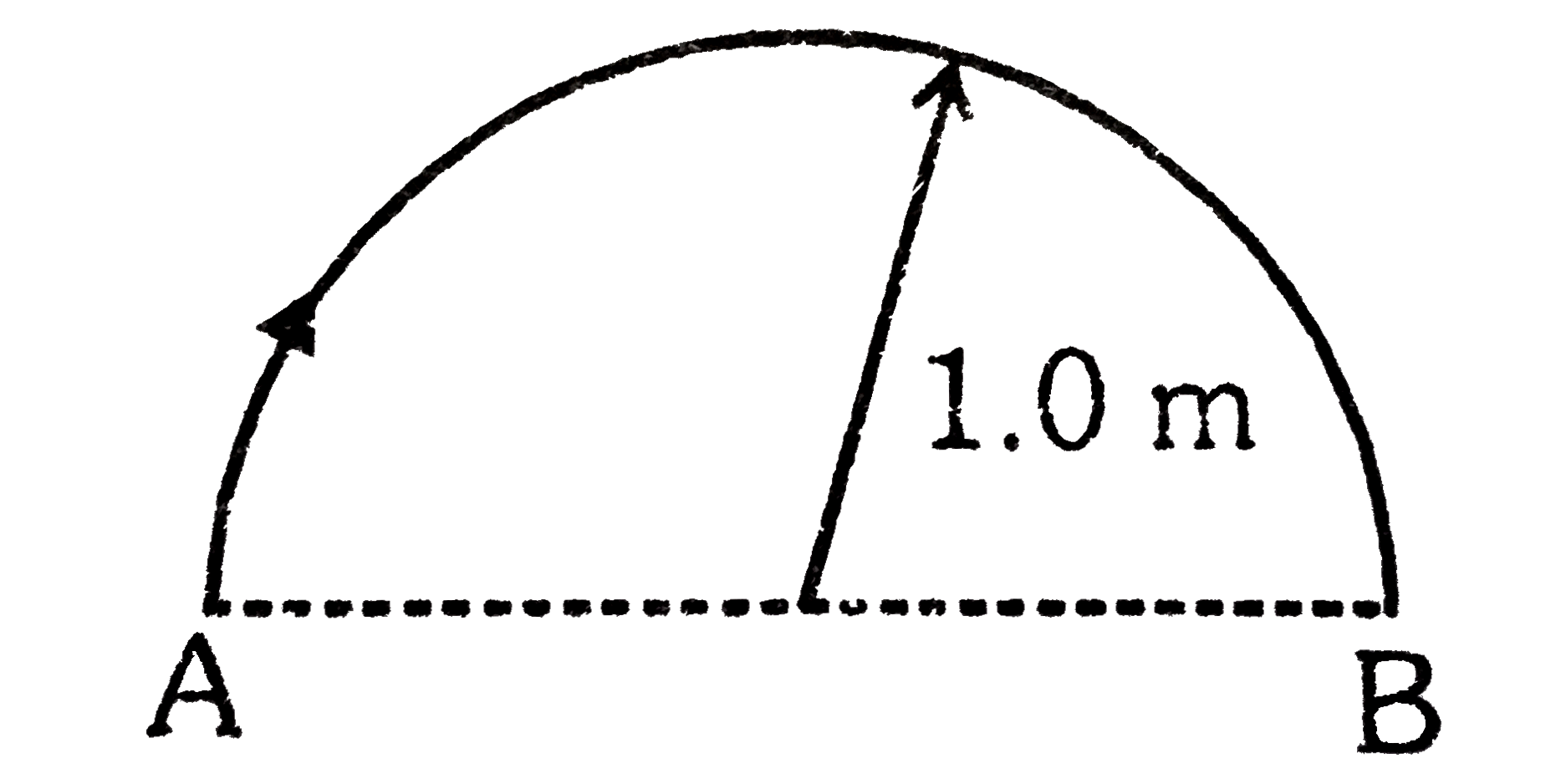
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionThe coordinate of a particle moving in a plane are given by x(t) = a cos (pt) and y(t) = b sin (pt) where a,b (lt a) and P are positive constants of appropriate dimensions . Then
View SolutionPosition of a particle moving along straight line is given by x(t)=AB(1−e−At), where B is constant and A>0. Dimension of A3B is similar to :−
View Solutionकिसी तल में गतिमान एक कण के निर्देशांक x(t)=acospt तथा y(t)=bsinpt है, जहाँ a,b(b<a) तथा p उपयुक्त विमाओं वाले धनात्मक नियतांक है तब
View SolutionThe coordinates of a particle moving in a plane are given by x(t) = acos(pt) and y(t) = bsin(pt) where a,b(< a) and p are positive constants of appropriate dimensions.Then
View SolutionFor a particle moving in the x-y plane, the x and y coordinates are changing as x=a sin omega t and y = a ( 1-cos omega t ) , where 'a' and omega constants. Then, what can be inferred for the trajectory of the particle ?
View Solutionएक कण का विस्थापन y=AsinPT+BcosPT द्वारा दर्शाया गया है। यह कण
View SolutionIf x=sint,y=cospt then...
View SolutionThe coordinates of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt)" where "a,b(lta)andp are positive constants of appropriate dimensions. Then
View SolutionThe position of moving point in xy plane at time 't' is given by (ucosαt,usinα(t−pt2)) where u,α,p are constants . Find the equation of locus of the moving point.
View Solutionयदि x=sint,y=cospt, तब
View Solution
